【算法】合唱队形问题&最大上升子序列 详细代码＋分析（C++）

在线判题通道:牛客网-HJ24 合唱队

题目描述：

N 位同学站成一排，音乐老师要请最少的同学出列，使得剩下的 K 位同学排成合唱队形。

通俗来说，能找到一个同学，他的两边的同学身高都依次严格降低的队形就是合唱队形。

例子：

123 124 125 123 121 是一个合唱队形

123 123 124 122不是合唱队形，因为前两名同学身高相等，不符合要求

123 122 121 122不是合唱队形，因为找不到一个同学，他的两侧同学身高递减。

你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

注意：不允许改变队列元素的先后顺序 且 不要求最高同学左右人数必须相等

输入描述：

用例两行数据，第一行是同学的总数 N ，第二行是 N 位同学的身高，以空格隔开

输出描述：

最少需要几位同学出列

示例1

输入：

8

186 186 150 200 160 130 197 200

输出：

4

说明：

由于不允许改变队列元素的先后顺序，所以最终剩下的队列应该为186 200 160 130或150 200 160 130

代码（详细注释代码在下面）：

#include<bits/stdc++.h>
using namespace std;
int n,a[3001],f1[3001],f2[3001],MAX;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)    {
        cin>>a[i];
        f1[i] = 1;
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
            {
                f1[i]=max(f1[i],f1[j] + 1);                
            }
        }

    }
    for(int i=n;i>=1;i--)
    {
        f2[i] = 1;
        for(int j=n;j>i;j--)
        {
            if(a[j]<a[i])
            {
                f2[i] = max(f2[i], f2[j] + 1);
            }
        }
        MAX=max(MAX,f1[i]+f2[i]-1);
    }
    cout<<n-MAX<<endl;
    return 0;
 } 

题解+详细注释版代码

合唱队问题归结下来是求两个最大上升子序列的长度问题，从队列正方向得到所有的最大上升子序列，再从反方向得到所有的最大上升子序列（即为最大下降子序列），找出两个组合起来总长度最大的情况即为最终答案，所以问题简化为求最大上升子序列的问题。

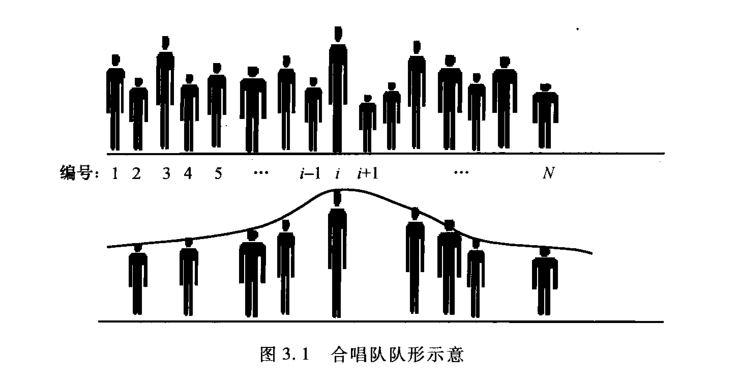
首先这个是课本上的内容，已经介绍的非常详细，如果看不太懂的话建议配合课本给出的例题，推算一下实际每步产生的队列是哪几个具体的同学，就会非常清晰了

如何理解代码&我遇到的问题&解决思路&代码理解

下面我就带着大家，从我当时理解算法&写代码的时候遇到问题问题出发，带大家理解一下代码

我的在coding过程中的最大问题不是对最大上升子序列的理解没到位，所以上面的介绍就简单过，主要是下面谈一下我遇到的代码上的最大的问题：

问题：在寻找最大上升子序列时 书上的动归方程给出的是

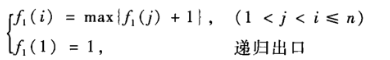
但是实际在代码中，没有能对一个集合内多个元素同时求出一个最大值的操作 所以需要使用一个循环来遍历实现，我就是在这个循环的地方卡了很久的理解：

    for(int i=1;i<=n;i++)    {
        cin>>a[i];
        f1[i] = 1;//问题①：方程中只给出了f1[1] = 1的递归出口
        //但是在代码中是将所有的f1[i]的初始值都给成了1
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
            {
                f1[i]=max(f1[i],f1[j] + 1);
                //问题②：一直不能理解这个地方，只求了两个数对比的最大值，如果出现1 2 5 3这样的串
                //那么是不是再次到3的时候 因为5 > 3 所以f1[4]的值只能为1了             
            }
        }

然后我想着搞不懂就自己推一遍过程

于是得到了答案：

问题①：给数组内所有元素赋值为1是为了防止出现如2 5 1这样的排列的时候到了第三个同学高度为1 则此时最大上升子序列的值应该为1，如果不整体赋初值的话，到第三个同学这里，上升序列的长度就是0了

但是这好像仍然不能解决问题②，于是我研究了下这个循环

这里使用了循环for(int j=1;j<i;j++) 遍历了所有的a[j]与a[i]比较 就是为了保证不会出现1 2 5 3的情况时

a[3] = 5 > a[4] = 3 导致f[4] = 1

而使用循环会保证和前面所有的上升子串都进行了一次比较

j=1:a[1] < a[4] = 3 --> f[4] = f1[1] + 1 = 2

表示序列f1[1] + 第4个同学可以组成新序列1 3且长度为2

j=2:a[2] < a[4] = 3 --> f[4] = f1[2] + 1 = 3

表示序列f2[1] + 第4个同学可以组成新序列1 2 3且长度为3

j=1:a[3] > a[4] = 3 --> f[4] = f1[2] = 3

5 > 3 则第三个序列f[3]无法和第4个同学组成新序列 序列长度还是之前的3

得出序列f[4]最大值为3

所以for(int j=1;j<i;j++) 这个j循环就是负责了这个集合中找最大值的功能，对应了方程

f1[j]代表到第j个同学的最大上升子串 则为了求集合最大值 使用了一次循环遍历

如果a[i] > a[j]说明第i个同学要比第j个同学 和第j个同学已经建立起的上升子序列中所有同学都高，则上升子序列的最大值，就可以更新为已经建立的上升子序列f1[j]加上同学a[i] 表示为f1[j] + 1

详细注释版代码

#include<bits/stdc++.h>
using namespace std;
int n,a[3001],f1[3001],f2[3001],MAX;//f1[i]表示上升子序列的个数 f2[i]表示反方向开始的上升子序列的个数


int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)//下标从1开始
    {
        cin>>a[i];
        f1[i] = 1;//这里很关键 递归边界是f[1] = 1 以及每个上升子序列的最小值为1
        //但是给数组内所有元素赋值为1是为了防止出现如2 5 1这样的排列的时候
        //到了第三个同学高度为1 则此时最大上升子序列的值应该为1
        for(int j=1;j<i;j++)//利用循环求集合中的最大值max{f[j] + 1}需要循环 因为程序只能求两者最大值
        {
            if(a[j]<a[i])//如果a[i]比a[j]高 则说明出现了更高的同学 上升子序列可以增加
            //但是这里注意 j是从1开始遍历到i-1 说明是从a[j]开始 一个一个与a[i]比较了
            //f[j]代表到第j个同学的最大上升子串 则为了求集合最大值 使用了一次循环遍历
            //如果a[i] > a[j]说明第i个同学要比第j个同学 和第j个同学已经建立起的上升子序列中所有同学都高
            {
                f1[i]=max(f1[i],f1[j] + 1);             
                //则上升子序列的最大值，就可以更新为已经建立的上升子序列f[j]加上同学a[i] 表示为f[j] + 1
                //整个for j 循环满足动归方程 f[i] = max{f[j] + 1} (1 < j < i <= n)
            }
            //但是这里使用了循环 遍历了所有的a[j]与a[i]比较 就是为了保证不会出现1 2 5 3的情况时
            //a[3] = 5 > a[4] = 3 导致f[4] = 1
            //而使用循环会保证和前面所有的上升子串都进行了一次比较
            //j=1:a[1] < a[4] = 3 --> f[4] = f1[1] + 1 = 2
            //表示序列f1[1] + 第4个同学可以组成新序列1 3且长度为2
            //j=2:a[2] < a[4] = 3 --> f[4] = f1[2] + 1 = 3
            //表示序列f2[1] + 第4个同学可以组成新序列1 2 3且长度为3
            //j=1:a[3] > a[4] = 3 --> f[4] = f1[2] = 3
            //5 > 3 则第三个序列f[3]无法和第4个同学组成新序列 序列长度还是之前的3
            //得出序列f[4]最大值为3
        }
    }

    for(int i=n;i>=1;i--)
    {
        f2[i] = 1;
        for(int j=n;j>i;j--)
        {
            if(a[j]<a[i])
            {
                f2[i] = max(f2[i], f2[j] + 1);
            }
        }
        MAX=max(MAX,f1[i]+f2[i]-1);//遍历所有的f1和f2算出最大值
        //因为上升和下降的个数都包括了最高点的同学，所以减去一个
    }
    cout<<n-MAX<<endl;
    return 0;
 }