前言
🌟🌟本期讲解关于力扣的几篇题解的详细介绍~~~
🌈感兴趣的小伙伴看一看小编主页:GGBondlctrl-CSDN博客
🔥 你的点赞就是小编不断更新的最大动力
🎆那么废话不多说直接开整吧~~

目录

——前言:关于堆这个数据结构,想必大家多多少少已经了解,并熟悉过了;其中最经典的问题就是使用堆来解决TOPK问题,但是除次之外,堆的构建以及堆来求解中位数,那么不知道大家了解过没有~~~
📚️1.前K个高频单词
🚀1.1题目描述
给定一个单词列表 words 和一个整数 k ,返回前 k 个出现次数最多的单词。
返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率, 按字典顺序 排序。
第一种情况:
输入: words = ["i", "love", "leetcode", "i", "love", "coding"], k = 2
输出: ["i", "love"] 解析: "i" 和 "love" 为出现次数最多的两个单词,均为2次。
注意,按字母顺序 "i" 在 "love" 之前。
第二种情况:
输入: ["the", "day", "is", "sunny", "the", "the", "the", "sunny", "is", "is"], k = 4
输出: ["the", "is", "sunny", "day"]
解析: "the", "is", "sunny" 和 "day" 是出现次数最多的四个单词,出现次数依次为 4, 3, 2 和 1 次
具体解析过后就是:求出现次数最多的单词,如果次数一样,就按照字典顺序进行排序操作~~
🚀1.2题目解析
看到前k个这个关键字,咱们想到的就是堆排。统计单词出现的个数,那么很明显就是使用哈希表来实现我们的单词和次数的存储,即一个字符串类型记录单词,一个整数类型记录出现的次数;
但是~~,本题最关键的问题就是,在满足两者次数相同的时候,这个按照字典序列进行排序,这个就是一个关键;
思路:
第一种情况:按照次数进行入堆的操作,那么我们要找次数大的那么就直接创建一个小根堆
第二种情况:遇到次数相同的,那么字典序小的在前面,那么创建一个大根堆

即找前几小的,创建大根堆;找前几大的,创建小根堆;
那么这里关键就是如何创建我们的堆了;
所以总结:
1.将我们的字符串数组遍历,将对应的字符串和次数存入哈希表中
2.依据条件创建我们的堆
3.遍历我们的哈希表存入我们的堆中
4.获取结果
🚀1.3代码编写
代码如下:
class Solution {
public List<String> topKFrequent(String[] words, int k) {
Map<String,Integer> map = new HashMap<>();
//遍历我们的字符数组进行添加
for(String s : words){
map.put(s, map.getOrDefault(s,0) + 1);
}
//创建我们的大小根堆
PriorityQueue<Pair<String,Integer>> heap = new PriorityQueue<>(
(a,b) ->{
if(a.getValue().equals(b.getValue())){
//如果次数相同,那么根据字典序比较大根堆
return b.getKey().compareTo(a.getKey());
}
return a.getValue() - b.getValue();
}
);
//遍历我们的哈希表,并存入我们的优先级队列中
for(Map.Entry<String,Integer> e : map.entrySet()){
heap.offer(new Pair<String,Integer>(e.getKey(),e.getValue()));
if(heap.size() > k){
heap.poll();
}
}
List<String> ret = new ArrayList<>();
//拿到数据
while(!heap.isEmpty()){
ret.add(heap.poll().getKey());
}
Collections.reverse(ret);
return ret;
}
}解释:
第一:在保存我们的字符串以及次数在哈希表中时,注意为0时的情况;
第二:在根据条件,通过lambda表达式创建我们的堆
第三:遍历哈希表中,存入堆中,要判断堆的长度
第四:保存我们的数据后,要记得翻转我们的列表
📚️2.数据流的中位数
🚀2.1题目描述
中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
- 例如
arr = [2,3,4]的中位数是3。 - 例如
arr = [2,3]的中位数是(2 + 3) / 2 = 2.5。
实现 MedianFinder 类:
-
MedianFinder()初始化MedianFinder对象。 -
void addNum(int num)将数据流中的整数num添加到数据结构中。 -
double findMedian()返回到目前为止所有元素的中位数。与实际答案相差10-5以内的答案将被接受。
当然其实就是三个函数:第一初始化我们的数据结构,第二添加我们的值到我们的数据结构中,第三返回我们数据结构中的中位数;
当然中位数就是:在一堆有序数中的中间值,若时偶数倍,那么就是中间两个值之和除以2;奇数倍即有序数中的中间那个值;(这个大家初中小学就应该学过了吧 ^ _ ^)
🚀2.2题目解析
2.2.1第一种思路
其实第一种思路其实非常简单,就是我们在每次加入数据后,对整个数组进行排序,然后在我们的找中间值的时候,我们根据我们数组的长度来进行判断(分为奇数,与偶数),然后获取我们的中位数;
如下图:
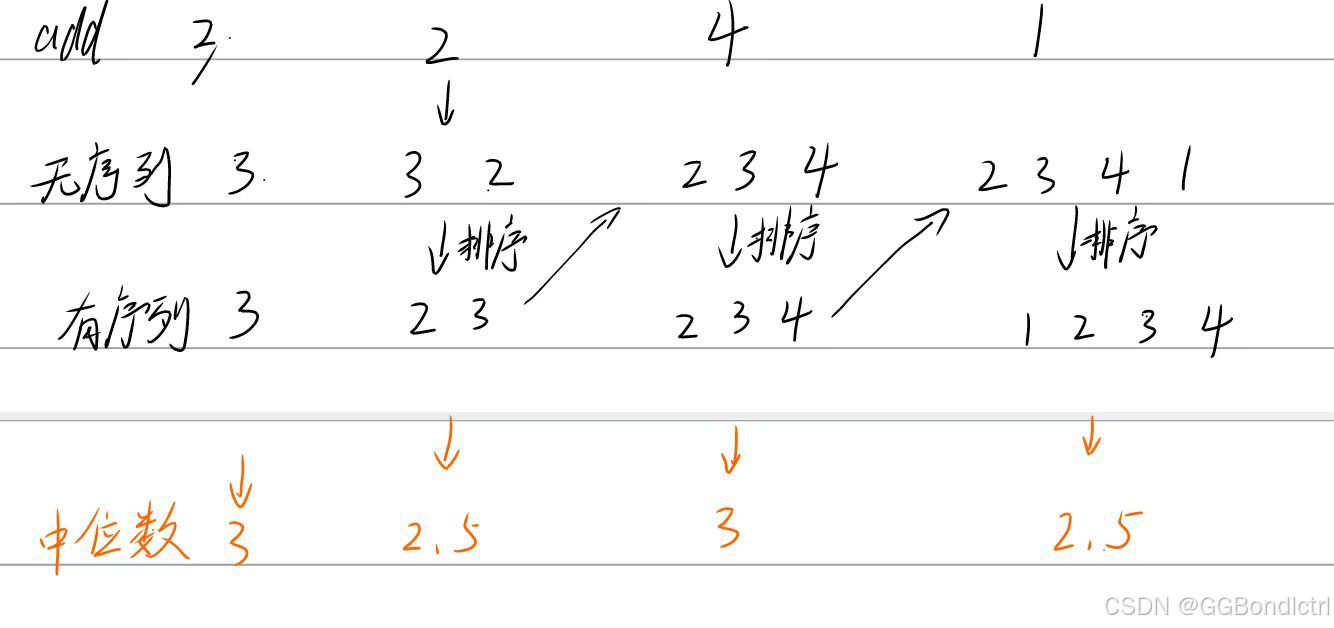
这里小编就不再过多解释了(肯定超时了)~~~
2.2.2第二种思路
第二种思路就是使用我们的堆来进行操作,是不是很意外;
我们思路就是:将整个有序数组分为两变;左边创建一个大根堆,右边创建一个小根堆;并且我们的两个堆的长度左边堆长度:m;右边堆长度:n
满足条件:m == n + 1或者m == n;
主要是为了在奇数长度下直接取左边大根堆对顶,偶数条件下取两个堆对顶然后除以2即可;
为啥呢?
1.我们的思路是在两个堆对顶进行中位值的获取,若不满足上述条件就会导致操作堆顶不能满足中位数获取~~~
2.我们拿到一个数该放入右边还是左边呢?这里我们统一按照大根堆对顶进行参照
3.假如m == n+1;但是要放入我们的m,那么此时咋办:
直接插入我们的大根堆,然后大根堆出堆放入我们小根堆,就可以完成堆的维护了
同理 m == n,如果要插入我们的小根堆,那么我们将小根堆的堆顶元素放入我们的大根 堆就可以了;
假如我们m == n + 1,但是此时哦们要插入大根堆,那么就要维护我们的两个堆,如下所示:
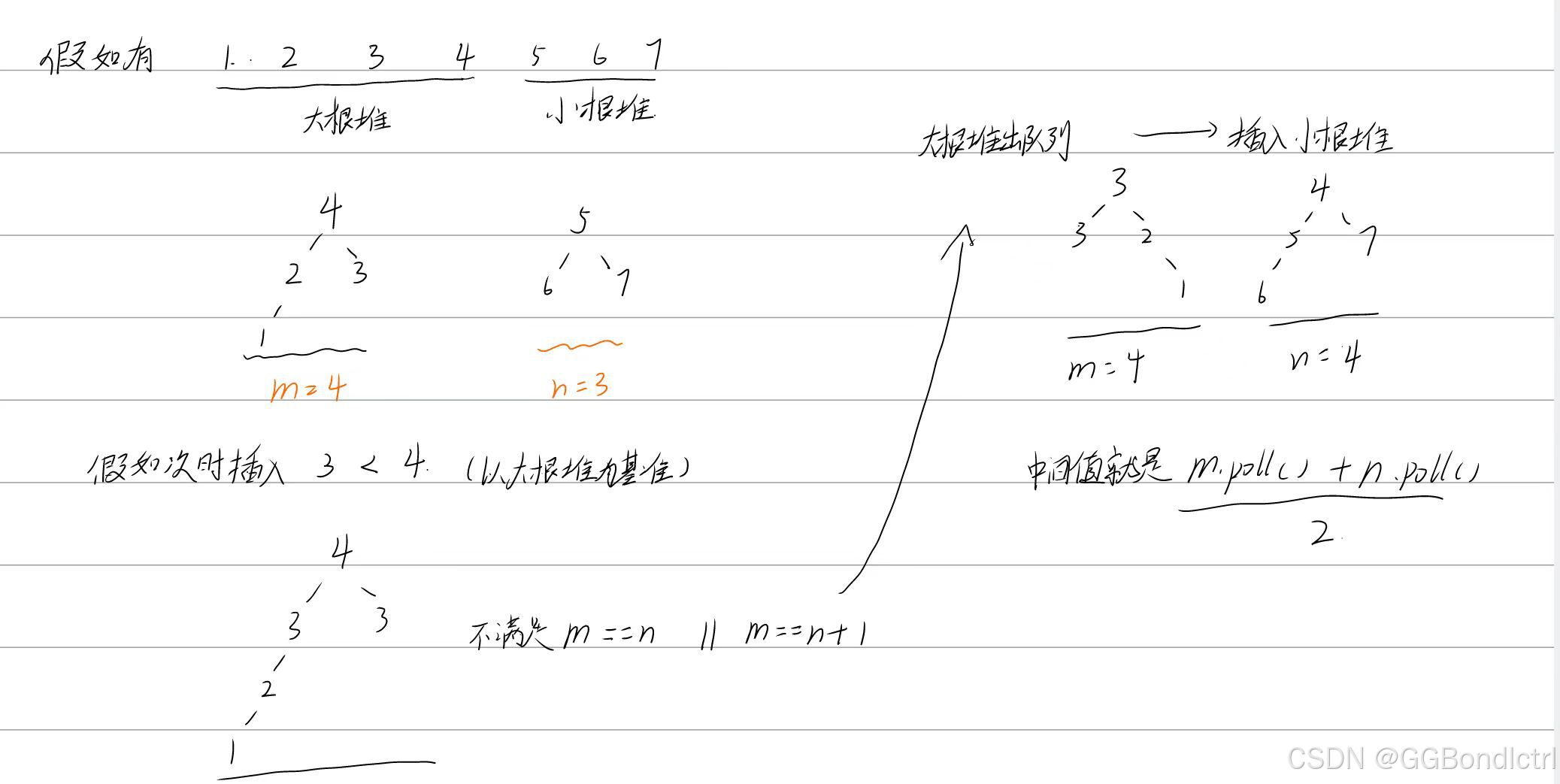
总结就是:
中间值,要靠两个堆对顶来进行获取;
不断在添加数值后,依据我们的m == n + 1或者m == n来进行堆的维护
🚀2.3代码编写
2.3.1第一种代码
如下所示:
class MedianFinder {
List<Integer> ret ;
public MedianFinder() {
ret = new ArrayList<>();
}
public void addNum(int num) {
ret.add(num);
//进行排序
Collections.sort(ret);
}
public double findMedian() {
double temp;
//进行取值判断
if(ret.size() %2 == 0){
int index = ret.size()/2;
temp = (double)(ret.get(index) + ret.get(index-1))/2;
}else{
int index = ret.size()/2;
temp = (double)(ret.get(index));
}
return temp;
}
}这里的排序是通过sort进行排序的哈~~~
2.3.2第二种代码
如下所示:
class MedianFinder {
//创建一个大根堆,小根堆
PriorityQueue<Integer> maxHeap;
PriorityQueue<Integer> minHeap;
public MedianFinder() {
maxHeap = new PriorityQueue<>((a,b) -> b-a);
minHeap = new PriorityQueue<>();
}
public void addNum(int num) {
//维护我们的大小堆
int m = maxHeap.size();
int n = minHeap.size();
if(m == n){
//进入左边
if(m == 0 || num <= maxHeap.peek()){
maxHeap.offer(num);
}else{
minHeap.offer(num);
int temp = minHeap.poll();
maxHeap.offer(temp);
}
}else if(m == n + 1){
if(num <= maxHeap.peek()){
maxHeap.offer(num);
int temp = maxHeap.poll();
minHeap.offer(temp);
}else{
minHeap.offer(num);
}
}
}
public double findMedian() {
double median;
if(maxHeap.size() == minHeap.size()){
median = (double)(maxHeap.peek() + minHeap.peek())/2;
}else{
median =(double) maxHeap.peek();
}
return median;
}
}
解释:
其实就是根据两个堆的长度是否满足我们上述分析的两种条件;我们每次插入数据时,都要peek一下我们大根堆的堆顶元素,插入后要判断是否会打断我们m == n || m == n + 1的条件,如若打乱了我们的条件,那么就要进行维护(将一个堆的堆顶,放入另一个堆即可)
最后在查找我们的中间值的时候,根据我们两个堆的长度进行判断我们应该取大根堆堆顶还是两个堆堆顶的和再除以2;
📚️3.总结
本期小编主要是针对力扣上两道关于堆的题目进行讲解:前K个高频单词,数据流的中位数;
692. 前K个高频单词 - 力扣(LeetCode)
🌅🌅🌅~~~~最后希望与诸君共勉,共同进步!!!

💪💪💪以上就是本期内容了, 感兴趣的话,就关注小编吧。
😊😊 期待你的关注~~~

























 350
350

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








