图论模型
基础理论
1.无向图与有向图
- 有向图的边称为弧,有向图一般记为 D=(V,A)D=(V,A)D=(V,A),其中 VVV 为顶点集,AAA 为弧集。
- 边的表示 (vi,vj)(v_i,v_j)(vi,vj),弧的表示 <vi,vj><v_i,v_j><vi,vj>。
2.简单图与完全图
- 无环且无重边的图称为简单图。
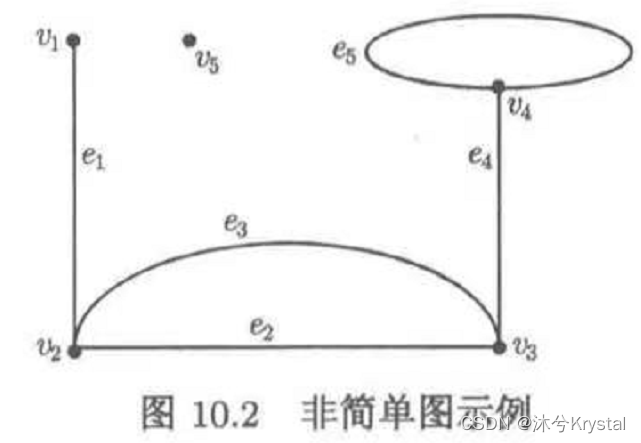
- 上图中,e2e_2e2 和 e3e_3e3 为重边, e5e_5e5 为环。
- 任意两点均相邻的简单图称为完全图。含 nnn 个顶点的完全图记为 KnK_nKn.
3.赋权图
- 赋权图中的权可以是距离、费用、时间、效益、成本等。
4.顶点的度
- 出度记为 d+(v)d^+(v)d+(v),入度记为 d−(v)d^-(v)d−(v).
- 度数为奇数的顶点称为奇顶点,度为偶数的顶点称为偶顶点。
定理 给定图 G=(V,E)G=(V,E)G=(V,E),所有顶点的度数之和是边数的2倍,即
∑v∈Vd(v)=2∣E∣ \sum_{v \in V} d(v)=2|E| v∈V∑d(v)=2∣E∣
5.子图
- 如果 G1G_1G1 是 G2G_2G2 的子图,且 V1=V2V_1=V_2V1=V2,则称 G1G_1G1 是 G2G_2G2 的生成子图。
6.道路与回路
- 设 W=v0e1v1e2...ekvkW=v_0e_1v_1e_2...e_kv_kW=v0e1v1e2...ekvk,路长为边的个数 kkk
- 各边相异的道路称为迹,各顶点相异的道路称为轨道。
- 以顶点 u,vu,vu,v 分别为起点和终点的最短轨道之长为顶点 u,vu,vu,v 的距离。
7.连通图与非连通图
- 如果无向图 GG





 本文介绍了图论的基本概念,包括无向图、有向图、简单图、完全图、赋权图和顶点度数。讨论了连通图、强连通图以及道路与回路的概念。此外,还深入讲解了图的表示方法,如关联矩阵和邻接矩阵。文章进一步探讨了最大流问题,包括可行流的条件以及如何通过线性规划求解最大流。最后,引入了最小费用流问题,阐述了在网络流中考虑费用的优化目标。
本文介绍了图论的基本概念,包括无向图、有向图、简单图、完全图、赋权图和顶点度数。讨论了连通图、强连通图以及道路与回路的概念。此外,还深入讲解了图的表示方法,如关联矩阵和邻接矩阵。文章进一步探讨了最大流问题,包括可行流的条件以及如何通过线性规划求解最大流。最后,引入了最小费用流问题,阐述了在网络流中考虑费用的优化目标。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 271
271










