常见的五种神经网络(4)-深度信念网络（上）篇之玻尔兹曼机和受限玻尔兹曼机

引言

常见的五种神经网络系列第三篇，主要介绍深度信念网络。内容分为上下两篇进行介绍，本文主要是深度信念网络（上）篇，主要介绍以下内容：

• 背景
• 玻尔兹曼机
• 受限玻尔兹曼机

该系列的其他文章：

• 常见的五种神经网络(1)-前馈神经网络
• 常见的五种神经网络(2)-卷积神经网络
• 常见的五种神经网络(3)-循环神经网络(上篇)
• 常见的五种神经网络(3)-循环神经网络(中篇)
• 常见的五种神经网络(3)-循环神经网络(下篇)
• 常见的五种神经网络(4)-深度信念网络(上篇)
• 常见的五种神经网络(4)-深度信念网络(下篇)
• 常见的五种神经网络(5)-生成对抗网络

背景

对于一个复杂的数据分布，我们往往只能观测到有限的局部特征，并且这些特征通常会包含一定的噪声。如果要对这个数据分布进行建模，就需要挖掘出可观测变量之间复杂的依赖关系，以及可观测变量背后隐藏的内部表示。

而深度信念网络可以有效的学习变量之间复杂的依赖关系。深度信念网络中包含很多层的隐变量，可以有效的学习数据的内部特征表示，也可以作为一种有效的非线性降维方法，这些学习到的内部特征表示包含了数据的更高级的、有价值的信息，因此十分有助于后续的分类和回归等任务。

玻尔兹曼机是生成模型的一种基础模型，和深度信念网络的共同问题是推断和学习，因为这两种模型都比较复杂，并且都包含隐变量，他们的推断和学习一般通过MCMC方法来进行近似估计。这两种模型和神经网络有很强的对应关系，在一定程度上也称为随机神经网络（Stochastic Neural Network，SNN）。

因为深度信念网络是有多层玻尔兹曼机组成的，所以本篇文章我们先来了解一下玻尔兹曼机和受限玻尔兹曼机。

玻尔兹曼机

介绍

玻尔兹曼机（Boltzmann Machine）可以看作是一种随机动力系统，每个变量的状态都以一定的概率受到其他变量的影响。玻尔兹曼机可以用概率无向图模型来描述，如下所示：

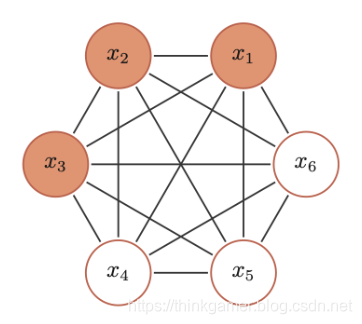
BM的三个性质：

• 二值输出：每个随机变量可以用一个二值的随机变量表示
• 全连接：所有节点之间是全连接的
• 权重对称：每两个变量之间的相互影响是对称的

BM中的每个变量$X$的联合概率由玻尔兹曼分布得到，即：
$$p(x)=\frac{1}{Z}exp(\frac{-E(x)}{T})$$
其中$Z$为配分函数，能量函数$E(X)$的定义为：
$$E(x)\stackrel{△}{=}E(X=x)=-(\sum _{i<j}{w}_{ij}{x}_i{x}_j+\sum _i{b}_i{x}_i)$$

其中$w_{ij}$是两个变量之间的连接权重， x i ∈ { 0 , 1 } x_i \in \{0,1\} xi​∈{0,1}表示状态，$b_i$是变量$x_i$的偏置。

玻尔兹曼机可以用来解决两类问题，一是搜索问题，当给定变量之间的连接权重，需要找到一组二值变量，使得整个网络的能量最低。另一类是学习问题，当给定一部分变量的观测值时，计算一组最优的权重。

生成模型

在玻尔兹曼机中配分函数$Z$通常难以计算，因此联合概率分布$p(x)$一般通过MCMC（马尔科夫链蒙特卡罗，Markov Chain Monte Carlo）方法来近似，生成一组服从$p(x)$分布的样本。这里介绍基于吉布斯采样的样本生成方法。

1. 全条件概率
吉布斯采样需要计算每个变量$X_i$的全条件概率$p(x_i|x_{\setminus i})$，其中$x_{\setminus i}$表示除了$X_i$外其它变量的取值。

对于玻尔兹曼机中的一个变量$X_i$，当给定其他变量$x_{\setminus i}$时，全条件概率公式$p(x_i|x_{\setminus i})$为：
$$\begin{gathered} p(x_i=1|x_{\setminus i})=\sigma (\frac{{\sum }_j{w}_{ij}{x}_j+b_i}{T}) \\ p(x_i=0|x_{\setminus i})=1-p(x_i=1|x_{\setminus i}) \end{gathered}$$
其中$\sigma (.)$为sigmoid函数。

2. 吉布斯采样

玻尔兹曼机的吉布斯采样过程为：随机选择一个变量$X_i$，然后根据其全条件概率$p(x_i|x_{\setminus i})$来设置其状态，即以$p(x_i=1|x_{\setminus i})$的概率将变量$X_i$设为1，否则全为0。在固定温度$T$的情况下，在运动不够时间之后，玻尔兹曼机会达到热平衡。此时，任何全局状态的概率服从玻尔兹曼分布$p(x)$，只与系统的能量有关，与初始状态无关。

要使得玻尔兹曼机达到热平衡，其收敛速度和温度$T$相关。当系统温度非常高$T\to \infty$时，$p(x_i|x_{\setminus i})\to 0.5$，即每个变量状态的改变十分容易，每一种系统状态都是一样的，从而很快可以达到热平衡。当系统温度非常低$T\to 0$时，如果$\Delta E_i(x_{\setminus i})>0$，则$p(x_i|x_{\setminus i})\to 1$，如果$\Delta E_i(x_{\setminus i})<0$，则$p(x_i|x_{\setminus i})\to 0$，即：
$$x_i=\{\begin{array}{cc}1& if{\sum }_j{w}_{ij}{x}_j+b_i\ge 0\\ 0& otherwise\end{array}$$

因此，当$ \rightarrow 0$时，随机性方法变成了确定性方法，这时，玻尔兹曼机退化为一个Hopfield网络。Hopfield网络是一种确定性的动力系统，每次的状态更新都会使系统的能量降低；而玻尔兹曼机时一种随机性动力系统，每次的状态更新则以一定的概率使得系统的能力上升。

3. 能量最小化与模拟退火

要使得动力系统达到热平衡，温度$T$的选择十分关键。一个比较好的折中方法是让系统刚开始在一个比较高的温度下运行达到热平衡，然后逐渐降低直到系统在一个比较低的温度下达到热平衡。这样我们就能够得到一个能量全局最小的分布。这个过程被称为模拟退火（Simulated Annealing）。

模拟退火是一种寻找全局最优的近似方法。

受限玻尔兹曼机

介绍

全连接的玻尔兹曼机十分复杂，虽然基于采样的方法提高了学习效率，但在权重更新的过程中仍十分低效。在实际应用中，使用比较广泛的一种带限制的版本，即受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）是一个二分图结构的无向图模型，如下所示。

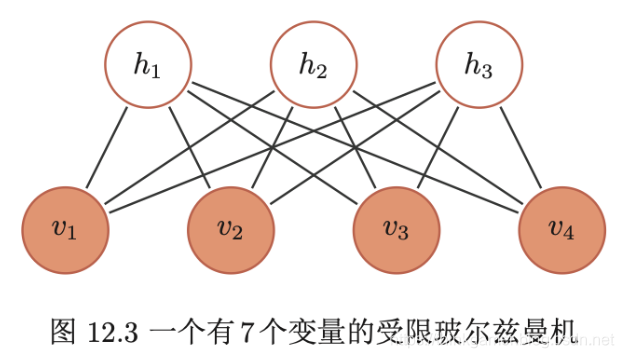
首先玻尔兹曼机中的变量也分为隐藏变量和可观测变量。分别用可观测层和隐藏层来表示这两组变量。同一层中的节点之间没有连接，而不同层一个层中的节点与另一层中的所有节点连接，这和两层的全连接神经网络结构相同。

一个受限玻尔兹曼机由$m_1$个可观测变量和$m_2$个隐变量组成，其定义如下：

• 可观测的随机向量$v=[v_1,...,v_{m_1}{]}^T$
• 隐藏的随机向量 $h=[h_1,...,h_{m_2}{]}^T$
• 权重矩阵$W\in R^{m_1\ast m_2}$，其中每个元素$w_{ij}$为可观测变量$v_i$和隐变量$h_j$之间边的权重
• 偏置$a\in R^{m_1}$和$b\in R^{m_2}$，其中$a_i$为每个可观测变量$v_i$得偏置，$b_j$为每个隐变量$h_j$得偏置

受限玻尔兹曼机得能量函数定义为：
$$E(v,h)=-\sum _i{a}_i{v}_i-\sum _j{b}_j{h}_j-\sum _i\sum _j{v}_i{w}_{ij}{h}_j=-a^{T}v-b^{T}h-v^{T}Wh$$
受限玻尔兹曼机得联合概率分布为$p(v,h)$定义为：
$$p(v,h)=\frac{1}{Z}exp(-E(v,h))=\frac{1}{Z}exp(a^{T}v)exp(b^{T}h)exp(v^{T}Wh)$$
其中$Z={\sum }_{v,h}exp(-E(v,h))$为配分函数。

生成模型

受限玻尔兹曼机得联合概率分布p(v,h)一般也通过吉布斯采样的方法来近似，生成一组服从$p(v,h)$分布的样本。

1. 全条件概率
吉布斯采样需要计算每个变量$V_i$和$H_j$的全条件概率。受限玻尔兹曼机中的同层的变量之间没有连接。从无向图的性质可知，在给定可观测变量时，隐变量之间相互条件独立，同样在给定隐变量时，可观测变量之间也相互条件独立，即有：
$$\begin{gathered} p(v_i|v_{\setminus i},h)=p(v_i|h) \\ p(h_j|v,h_{\setminus j})=p(h_j|v) \end{gathered}$$
其中$v_{\setminus i}$表示除变量$V_i$外其他可观测变量得取值，$h_{\setminus j}$为除变量$H_j$外其它隐变量的取值。因此，$V_i$的全条件概率只需要计算$p(v_i|h)$，而$H_j$的全条件概率只需要计算$p(h_j|v)$

在受限玻尔兹曼机中，每个可观测变量和隐变量的条件概率为：
$$\begin{gathered} p(v_i=1|h)=\sigma (a_i+\sum _j{w}_{ij}{h}_j) \\ p(h_j=1|v)=\sigma (b_j+\sum _i{w}_{ij}{v}_i) \end{gathered}$$

其中$\sigma$为sigmoid函数。

2. RBM中得吉布斯采样
受限玻尔兹曼机得采样过程如下：

• （给定）或随机初始化一个可观测的向量$v_0$，计算隐变量得概率，并从中采样一个隐向量$h_0$
• 基于$h_0$，计算可观测变量得概率，并从中采样一个个可观测的向量$v_1$
• 重复$t$次后，获得$(v_t,h_t)$
• 当$t\to \infty$时，$(v_t,h_t)$的采样服从$p(v,h)$分布

下图为上述采样过程的示例：

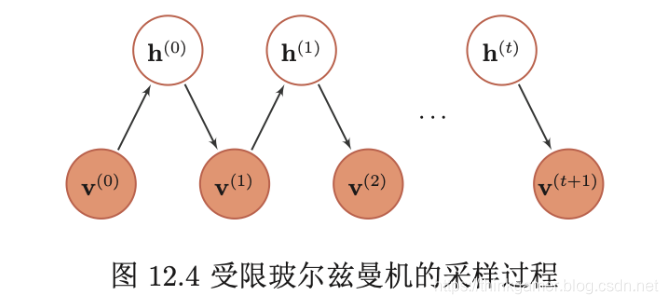
3. 对比散度学习算法

由于首先玻尔兹曼机得特殊结构，因此可以使用一种比吉布斯采样更高效的学习算法，即对比散度（Contrastive Divergence）。对比散度算法仅需k步吉布斯采样。

为了提高效率，对比散度算法用一个训练样本作为可观测向量的初始值，然后交替对可观测向量和隐藏向量进行吉布斯采用，不需要等到收敛，只需要k步就行了。这就是CD-k算法，通常，k=1就可以学得很好。对比散度得流程如下所示：

4. 受限玻尔兹曼机得类型
在具体的不同任务中，需要处理得数据类型不一定是二值得，也可能时连续值，为了能够处理这些数据，就需要根据输入或输出得数据类型来设计新的能量函数。一般来说受限玻尔兹曼机有以下三种：

• “伯努利-伯努利”受限玻尔兹曼机：即上面介绍得可观测变量喝隐变量都为二值类型得受限玻尔兹曼机
• “高斯-伯努利”受限玻尔兹曼机：假设可观测变量为高斯分布，隐变量为伯努利分布，其能量函数定义为：
  $$E(v,h)=\sum _i\frac{(v_i-{\mu }_i{)}^2}{2{\sigma }_i^2}-\sum j{b}_j{h}_j-\sum _i\sum j\frac{v_i}{{\sigma }_i}{w}_{i}j{h}_j$$
  其中每个可观测变量$v_i$服从$({\mu }_i,{\sigma }_i)$的高斯分布。
• “伯努利-高斯”受限玻尔兹曼机：假设可观测变量为伯努利分布，隐变量为高斯分布，其能量函数定义为：
  $$E(v,h)=\sum _i{a}_i{v}_j-\sum _j\frac{(h_j-u_j{)}^2}{2{\sigma }_j^2}-\sum _i\sum _j{v}_i{w}_{ij}\frac{h_j}{{\sigma }_j}$$
  其中每个隐变量$h_j$服从$({\mu }_j,{\sigma }_j)$的高斯分布

---

【技术服务】，详情点击查看： https://mp.weixin.qq.com/s/PtX9ukKRBmazAWARprGIAg

---

扫一扫 关注微信公众号！号主 专注于搜索和推荐系统，尝试使用算法去更好的服务于用户，包括但不局限于机器学习，深度学习，强化学习，自然语言理解，知识图谱，还不定时分享技术，资料，思考等文章！

---