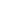dfs深度优先搜索探究迷宫的最短路径（C++）

最新推荐文章于 2024-08-01 23:45:28 发布

云㞬

最新推荐文章于 2024-08-01 23:45:28 发布

阅读量4k

点赞数 7

文章标签： c++ dfs 深度优先

本文链接：https://blog.csdn.net/GoiDKIE/article/details/124205780

版权

本文详细介绍了如何使用C++编程实现寻找6x6迷宫的最短路径算法，包括深度优先搜索（DFS）策略和路径保存。通过二维数组表示迷宫，并利用pair保存坐标，最终找到并输出最短路径及其长度。代码中还提供了针对不同方向的递归探索以及如何判断和更新最短路径长度。

摘要由CSDN通过智能技术生成

以下有个 6*6 的迷宫

6 6
0 1 0 0 1 0
0 0 0 0 0 1
1 0 1 1 0 0
0 0 0 1 0 0
0 1 0 0 0 1
0 0 0 1 0 0

根据上图寻找的最短路径如下：

按照红色路径走时的坐标如下

(0,0) -> (1,0) -> (1,1) -> (1,2) -> (1,3) -> (1,4) -> (2,4) -> (3,4) -> (4,4) -> (5,4) -> (5,5)

按照蓝色路径走时的坐标如下

(0,0) -> (1,0) -> (1,1) -> (2,1) -> (3,1) -> (3,2) -> (4,2) -> (4,3) -> (4,4) -> (5,4) -> (5,5)

设计一个这样子的算法，保存的是探索过程所通过并且最后成功到达右下角出口的路线的每一个点的坐标，需要用到C++这样的函数

make_pair(x,y)；

pair(x,y)；

作为保存探索过程成对坐标的关键。

保存这样的成对的坐标的数组如下：

vector<pair<int,int>> oop; //保存的是一条完整的成功的路径的数组

vector<vector<pair<int,int>>> temp; //保存的是所有成功的路径的数组

其中temp数组是个二维数组，行作为一条路径，该行的列保存该路径的所有的点的坐标，那么判断路径是否为最短，只需要遍历每行判断找出最短。

在每条路径的探索当中，需要对路线进行已访问的设置，如下数组：

vector<vector<bool>> visit;

分下 -> 上 -> 右 -> 左递归进行探索（可换）

    dfs(min_way,a,i+1,j,visit,n,m,oop,temp);        //分下 -> 上 -> 右 -> 左四个方向查找
    dfs(min_way,a,i-1,j,visit,n,m,oop,temp);
    dfs(min_way,a,i,j+1,visit,n,m,oop,temp);
    dfs(min_way,a,i,j-1,visit,n,m,oop,temp);

输出路径版的代码如下：

//迷宫的最短路径问题

#include<iostream>
#include<vector>

using namespace std;                        
//注意此处的oop应该每次递归进入的空间的都是不同的，同时visit也是一样的，不能各个空间公用，应当独立
//所以每个递归空间的寻路的路径长度都是单独的，所以不能用&oop，容易造成数据错误
void dfs(int & min_way,int a[][10],int i,int j,vector<vector<bool>> visit,int n,int m,vector<pair<int,int>> oop,vector<vector<pair<int,int>>> & temp)
{
    if(i<0 || i>=n || j<0 || j>=m || visit[i][j] || a[i][j]==1)
    {
        return;
    }
    if(!visit[i][j])
    {
        oop.push_back(make_pair(i,j));
    }
    visit[i][j] = true;
    if(i == n-1 && j == m-1)
    {
        temp.push_back(oop);
        if(oop.size() < min_way)
        {
            min_way = oop.size();
        }
        return;
    }
    dfs(min_way,a,i+1,j,visit,n,m,oop,temp);        //分下 -> 上 -> 右 -> 左 四个方向查找
    dfs(min_way,a,i-1,j,visit,n,m,oop,temp);
    dfs(min_way,a,i,j+1,visit,n,m,oop,temp);
    dfs(min_way,a,i,j-1,visit,n,m,oop,temp);
}




int main(void)
{
    int n,m;
    cin >> n >> m;
    int a[10][10];
    vector<vector<bool>> visit;
    vector<pair<int,int>> oop;
    visit.resize(n,vector<bool>(m,false));
    vector<vector<pair<int,int>>> temp;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            cin >> a[i][j];
        }
    }
    int min_way=101;    //注意此处的oop应该每次递归进入的空间的都是不同的，
    dfs(min_way,a,0,0,visit,n,m,oop,temp);   
                //所以每个递归空间的寻路的路径长度都是单独的，所以不能用&oop，容易造成数据错误
    for(int i=0;i<temp.size();i++)
    {
        if(min_way == temp[i].size())
        {
            for(int j=0;j<temp[i].size();j++)
            {
                cout << temp[i][j].first << " " << temp[i][j].second << endl;
            }
        }
        cout << "-----" << endl;
    }
    return 0;
}

/*
 *
6 6
0 1 0 0 1 0
0 0 0 0 0 1
1 0 1 1 0 0
0 0 0 1 0 0
0 1 0 0 0 1
0 0 0 1 0 0

5 6
0 1 0 0 1 0
0 0 0 0 0 1
1 0 1 1 0 0
0 0 0 1 0 0
0 1 0 0 0 0
 */

输出情况如下：

当只需要单纯的输出最短路径的大小时：

只需要把源代码稍作修改，将temp如掉，每次oop.size()与min_way进行比较替换即可。

if(i == n-1 && j == m-1)
    {
        if(oop.size() < min_way)
        {
            min_way = oop.size();
        }
        return;
    }

迷宫最短路径纯输出最短路径长度的完整代码如下：



//迷宫最短路径问题，纯输出路径版

#include<iostream>
#include<vector>

using namespace std;                        
                //注意此处的oop应该每次递归进入的空间的都是不同的，同时visit也是一样的，不能各个空间公用，应当独立
                //所以每个递归空间的寻路的路径长度都是单独的，所以不能用&oop，容易造成数据错误
void dfs(int & min_way,int a[][10],int i,int j,vector<vector<bool>> visit,int n,int m,vector<pair<int,int>> oop)
{
    if(i<0 || i>=n || j<0 || j>=m || visit[i][j] || a[i][j]==1)
    {
        return;
    }
    if(!visit[i][j])
    {
        oop.push_back(make_pair(i,j));
    }
    visit[i][j] = true;
    if(i == n-1 && j == m-1)
    {
        if(oop.size() < min_way)
        {
            min_way = oop.size();
        }
        return;
    }
    dfs(min_way,a,i+1,j,visit,n,m,oop);
    dfs(min_way,a,i-1,j,visit,n,m,oop);
    dfs(min_way,a,i,j+1,visit,n,m,oop);
    dfs(min_way,a,i,j-1,visit,n,m,oop);
}




int main(void)
{
    int n,m;
    cin >> n >> m;
    int a[10][10];
    vector<vector<bool>> visit;
    vector<pair<int,int>> oop;
    visit.resize(n,vector<bool>(m,false));
//  vector<vector<pair<int,int>>> temp;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<m;j++)
        {
            cin >> a[i][j];
        }
    }
    int min_way=101;    //注意此处的oop应该每次递归进入的空间的都是不同的，
    dfs(min_way,a,0,0,visit,n,m,oop);  
             //所以每个递归空间的寻路的路径长度都是单独的，所以不能用&oop，容易造成数据错误
    cout << min_way << endl;
    return 0;
}

运行结果如下：