【数值分析】插值逼近法——三次样条插值函数

原创

已于 2024-11-06 13:34:56 修改 · 6.7k 阅读

54 ·

CC 4.0 BY-SA版权

文章标签：

#数据分析

于 2024-11-05 20:22:12 首次发布

· $M_{j}$ 的求法

前言

龙格现象

一般情况下，在利用多项式对某一函数近似逼近时，多项式的次数越高，需要的数据就越多，而预测也就越准确。随着多项式次数的增加，会出现插值结果偏离原函数的现像，这一现像称为龙格现象。

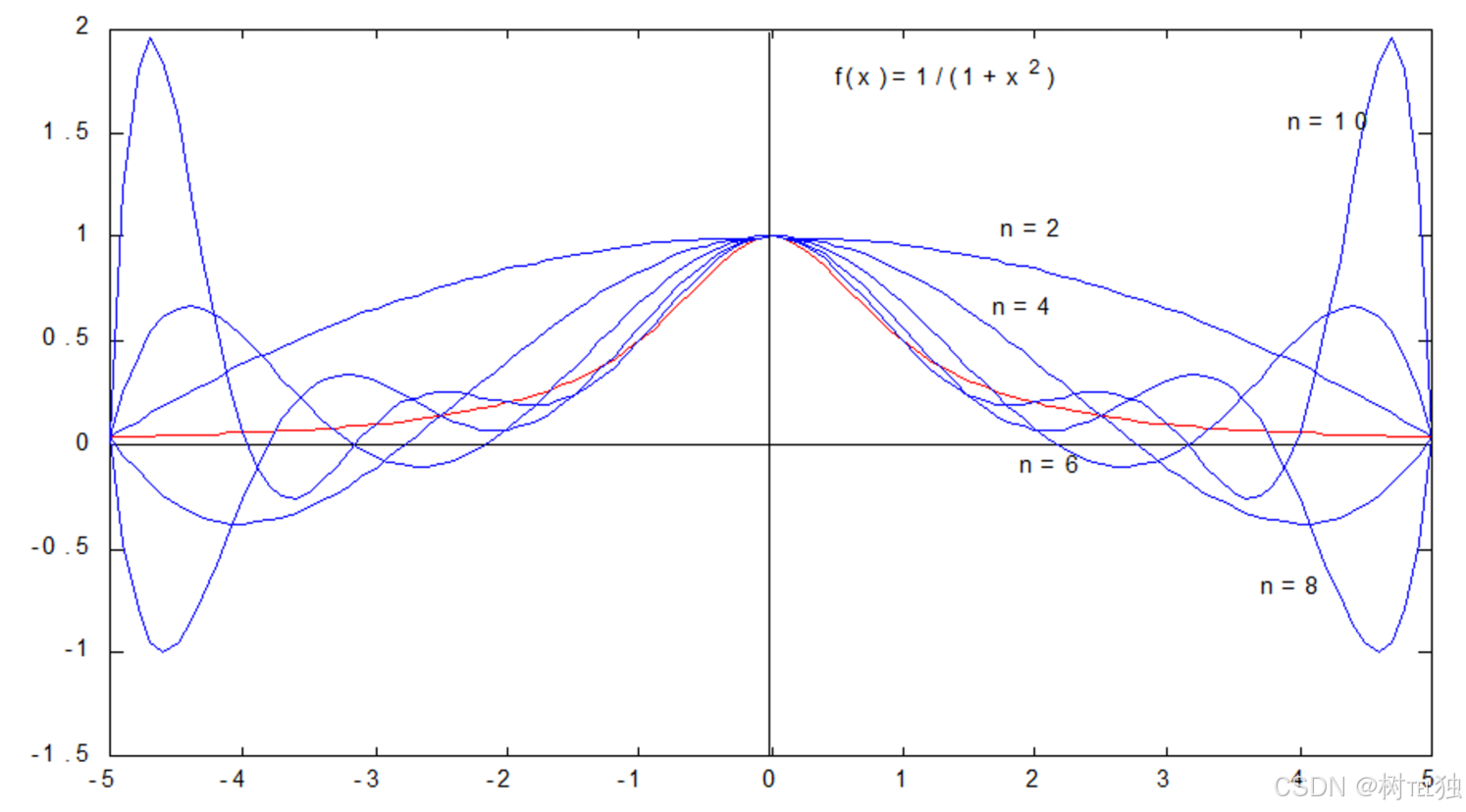
不同次数的Lagrange插值多项式的比较图

从图中可以看出高次插值多项式存在的缺陷

龙格现象产生的原因：误差由截断误差和舍入误差两部分组成，而在插值的计算过程中，增加插值多项式的次数可以减少截断误差，但舍入误差可能会扩散或放大。

样条函数

在数学学科的数值分析中，样条是一种特殊的函数，由多项式分段定义。

在实际生产生活中，类似于造船和工程制图时所需要的光滑度远大于简单分段插值函数的光滑度。因此需要一种新的方式，使得插值函数既是低阶分段函数又是光滑函数。因此数学家提出来样条函数。

样条函数：设 $S(x)$ 是区间 $[a,b]$ 上的函数，在区间 $[a,b]$ 上给定一组基点： $a=x_{0}<x_{1}<...<x_{n}=b$ ，若 $S(x)$ 满足条件

（1） $S(x)$ 在每个子区间 $[x_{i},x_{i+1}](i=0,1,2...,n-1)$ 上是次数不超过m的多项式；

（2） $S(x)$ 在区间 $[a,b]$ 上有m-1阶连续导数；

则称 $S(x)$ 是定义在区间 $[a,b]$ 上的m次样条函数。 $x_{0},x_{1},x_{2},...$ 称为样条节点，其中 $x_{1},...,x_{n-1}$ 称为内节点， $x_{0},x_{n}$ 称为边界节点。

分段线性函数为一次样条函数，而三次样条函数在工程中应用最广泛。

通常情况下：

（1）由一段一段的三次多项式曲线拼接而成的曲线；

（2）在拼接处，不仅函数是连续的，函数的一阶和二阶导数也是连续的。

三次样条插值函数

定义

设 $a=x_{0}<x_{1}<...<x_{N}=b$ 为区间 $[a,b]$ 的一个划分。如果分段函数 $S(x)$

$S(x)=\left\{\begin{matrix} S_{0}(x)&x\in[x_{0},x_{1}] \\ S_{1}(x)&x\in[x_{1},x_{2}]\\ ......\\ S_{N-1}(x)&x\in[x_{N-1},x_{N}] \end{matrix}\right.$

满足下述条件：

（1） $S(x),S^{''}(x),S^{'}(x)$ 都在区间 $[a,b]$ 上连续，即 $S(x)\in C^{2}[a,b]$ ；

（2） $S(x)$ 在每个小区间 $[x_{j},x_{j+1}]$ 上都是三次多项式；

则称 $S(x)$ 为区间 $[a,b]$ 上的三次样条函数。

若三次样条函数 $S(x)$ 满足插值条件 $S(x_{j})=y_{j}=f(x_{j}),j=0,1,...,N$ 则称 $S(x)$ 为 $f(x)$ 在 $[a,b]$ 上的三次样条插值函数。

存在性和唯一性

·存在性

$S(x)$ 除了满足基本插值条件 $S(x_{j})=f(x_{j})$ 外，还要满足条件：

$\left\{\begin{matrix} S_{i-1}(x_{i})=S_{i}(x_{i}), & i=1,2,...,n-1, \\ S^{'}_{i-1}(x_{i})=S^{'}_{i}(x_{i}), & i=1,2,...,n-1, \\ S^{''}_{i-1}(x_{i})=S^{''}_{i}(x_{i}) , & i=1,2,...,n-1. \end{matrix}\right.$

$S(x)=S_{j}(x)=a_{j}+b_{j}x+c_{j}x^{2}+d_{j}x^{3},x\in [x_{j},x_{j+1}],(j=0,...,n-1)$

共有4n个待定系数： $(a_{j}),({b_{j}}),(c_{j}),(d_{j}),j=0,1,...,n-1$ , $S(x)$ 需要有4n个独立条件确定

可利用条件：
①插值条件： $S(x_{j})=f(x_{j}),(j=0,1,...,n)$ 提供了n+1个独立条件；

②内部条件（光滑条件）： $\left\{\begin{matrix} S_{j-1}(x_{j})=S_{j}(x_{j})\\ S^{'}_{j-1}(x_{j})=S^{'}_{j}(x_{j})\\ S^{''}_{j-1}(x_{j})=S^{''}_{j}(x_{j}) \end{matrix}\right.$ $j=1,2,...,n-1$ ，给出了3（n-1）个条件。