最短路径问题：Dijkstra算法原理和证明

一、问题

最短路径问题：从一个有向图（或无向图）的某个顶点s出发，求到达其他任意一个顶点所经过的边的权重之和最小的路径。权重之和称为两个顶点之间的距离（距离均为正数）。

我们以无向图为例（顶点之间没有方向），每条边的权重可以使用权重矩阵W来描述，如有n个顶点，则权重矩阵大小为 n*n，W(i,j)为顶点i和j的直接相连的边的权重，如果没有直接相连，则赋值为无穷大。权重矩阵为对称矩阵。

二、算法

1、算法介绍

     Dijkstra算法与深度优先搜索类似，使用了贪心的思想，从一个顶点出发，每次查询所关联到的顶点的最短路径。

2、算法步骤

（1）定义变量：

定义一个数组dist，dist[m]表示顶点s到顶点m的最短距离。（在迭代过程中，里面的值可能不是最终最短距离，但是是当前考虑到已经扫描到的边的最短距离）

定义一个集合T，里面存放着已经查询到最终最短路径的顶点集合。

（2）初始化：

任取顶点 i，如果 s 和 i 直接相连，则dist[i]=W(s,i)，否则 W(s, i) 为无穷大。

T 集合只包含顶点 s。

（3）迭代：

A、从dist中找到最小值（除去集合 T 中包含的点），记为 dist[r]=d，然后将顶点 r 划入到集合 T 中。

B、对于每一个不属于集合 T 的点，比如顶点 q， 查看新加入的顶点 r 是否可以直接到达顶点 q，如果是，则比较通过顶点 r 到达顶点 q 的路径长度和当前的dist[q]值，然后取较小值，即 dist[q] := min(dist[r]+W(r, q), dist[q])

C、跳回到步骤A，直到所有的点都进入到了集合 T。

D、dist 中存放的值即为每个点的最终最短路径。

三、演示

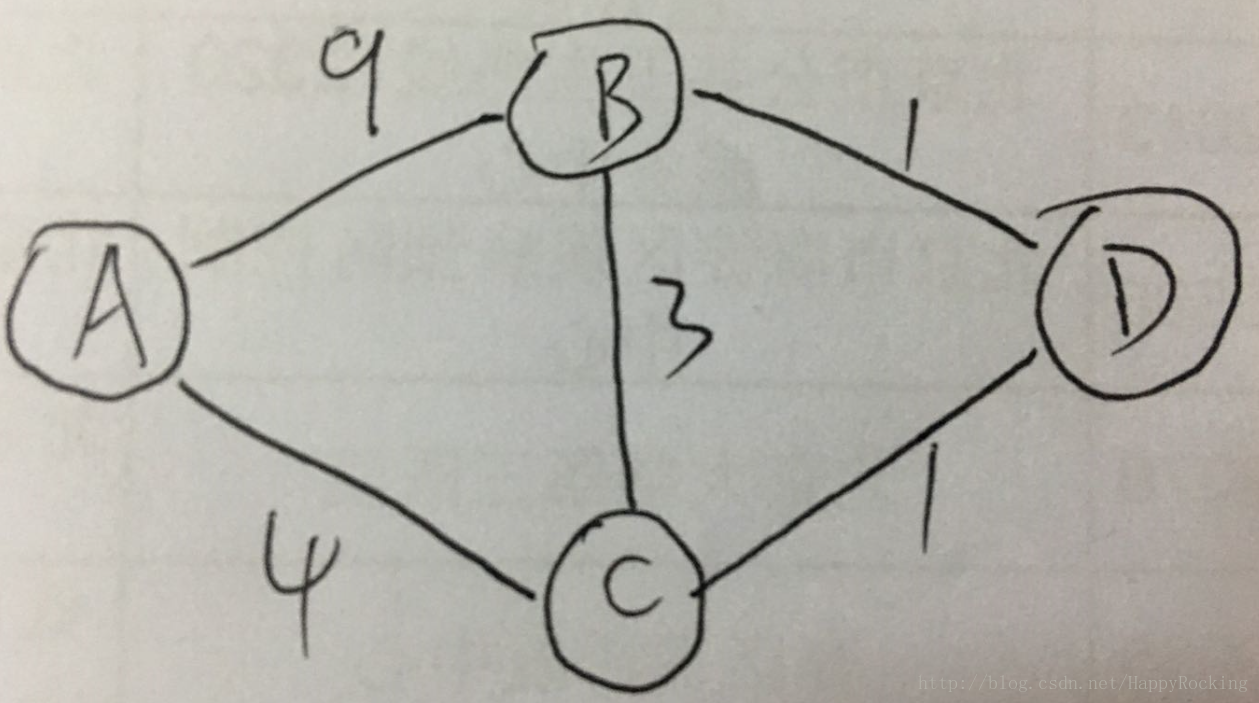
有4个点，A 为起点，要求从 A 分别到 B、C、D的最短路径。

1、初始化变量：

dist = [9, 4, ∞]，分别表示从源点到 B、C、D点的最短路径。

T = {A}

2、迭代：

（1）从dist不属于T的值中{9,4,∞}选一个最小值为4，对应点C，因此 T = {A,C}。

所有不属于集合T的点包括B、D。新加入的 C 可以直接到达 B，则 dist[B] := min(4+3,9)=7 ；新加入的 C 可以直接到达 D，则 dist[D] := min(4+1,∞)=5。因此 dist=[7,4,5]

（2）从dist不属于T的值中{9,5}选一个最小值为5，对应点D，因此 T = {A,C,D}

所有不属于集合T的点包括B。新加入的 D 可以直接到达 B，则 dist[B] := min(5+1,7)=6。因此 dist=[6,4,5]

（3）不属于T的只剩下B了， 直接加入到T即可。

（4）根据dist的值，从A点到B、C、D点的最短路径分别为：6、4、5

四、证明

推论1、如果只考虑集合 T 中包含的点，那么步骤A中 d 就是顶点 s 到 顶点 r 的最短距离（只考虑集合 T 的范围内的路径）。

证明：递归法证明：

（1）在第一次迭代中，dist初始化为直接与 s 相连的边的权重，明显最小权重的边连接的那个点为 s 到此点的最短距离。

（2）假如已经迭代完第 i 次，T 中包含了 i 个顶点（除了顶点s），dist 中包含了 i 个最终最短距离（还有其他不是无穷大的数值，但是不一定是最终最短距离），那么第 i+1 次的步骤A需要从 dist 中挑出除去这 i 个最短距离外的最小值，比如 dist[r]=d。因为前 i 次每次迭代中步骤B如果扫描到了与点 r 直接相连的点，都会比较一下经过此点到 r 的路径总长与当前已经存放的dist[r]的大小，即：

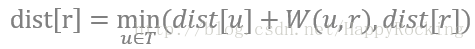
其中公式右边min内的 dist[r] 为 s 到 r 的直接距离，dist[u] 为集合 T 内 s 到 u 的最终最短距离。此公式恰好是在集合 T 的范围内计算从 s 到 r 的最短距离的方法，因此得证。

推论2、如果 r 点属于集合 T，且存在一个点 t，s.t. 从 s 到 t 的某条路径总长e < dist[r]，则 t 点一定也属于集合 T。

证明：不是一般性，我们把从 s 点分别到 t 点和 m 点的路径画出来：

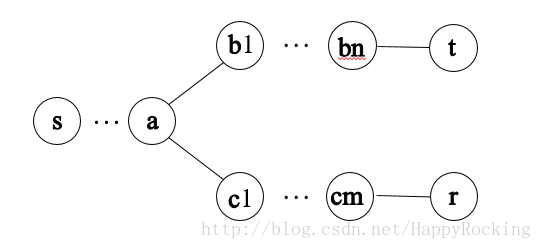
且 s →...→ a → b1 →...→ bn → t 的总长为 e， s →...→ a → c1 →...→ cm → r 的总长为 dist[r]。

我们定义 distance(bi) 为 s →...→ a → b1 →...→ bi 的路径总长，distance(cj) 为 s →...→ a → c1 →...→ cj 的路径总长。

（1）当 e 为 s 到 t 的最短距离时：当集合 T 包含 t 时，一定也包含了 s...a、b1~bn。

因为 r 属于 T，则一定存在某次迭代，s.t.  s 和 a 均包含于集合 T。继续迭代，每次可能会从 b 系列中选取点归入集合 T，可能会从 c 系列中选取点归入集合 T，也可能是其他点。由于 distance(t) = e < dist[r] = distance(r)，则一定存在点 ci，1≤i≤m，s.t. distance(ci) ≤ distance(t) 且 distance(c(i+1)) > distance(t)。（记 c(m+1)为r）。因此集合 T 中加入点的次序为 {ci, t} 早于 {c(i+1), r}。因此如果 r 属于集合 T，则 t 一定也属于集合 T，且比 r 先划入到集合 T。

（2）当 s 到 t 的最短距离 < e 时：s 到 t 的最短距离为 g，则 g < e，因此有 g < dist[r]。将 a、b1~bn 变为最短路径上的点，则变为了第（1）种情况。

推论3、步骤A中 d 就是顶点 s 到 顶点 r 的最终最短距离：

证明：假设 d 不是 s 到 r 的最终最短距离，根据推论1可知，s 到 r 的真正最终最短路径一定包含了集合 T 之外的点（记为 t），即 s →...→ t → ...→ r 的总长 < d。因为权重总是为正数，因此 s → ...→ t 的总长 < d，根据推论2可知， t 一定属于 T ，这与 t 不属于集合 T 矛盾。因此 d 是 s 到 r 的最终最短距离。

欢迎关注我的公众号：