文章目录
前言
一、离散时间信号
1. 基本概念
对模拟信号
x
a
(
t
)
x_a(t)
xa(t)进行等间隔采样,采样间隔为T,采样点对应的时刻为
t
=
n
T
t=nT
t=nT( n取整数),得到 [采样的数学模型]
x
a
(
t
)
∣
n
T
=
x
a
(
n
T
)
−
∞
<
n
<
+
∞
\begin{aligned} x_a(t)|_{nT} = x_a(nT) -\infty < n < +\infty \end{aligned}
xa(t)∣nT=xa(nT)−∞<n<+∞不同的n值
x
a
(
n
T
)
x_a(nT)
xa(nT)形成一个有序的数字序列:
…
,
x
a
(
−
T
)
、
x
a
(
0
)
、
x
a
(
T
)
,
…
,
…, x_a(-T)、x_a(0)、x_a(T),…,
…,xa(−T)、xa(0)、xa(T),…, 就是 时域离散信号 或 序列
注意:
- 实际中,数字序列值按顺序放在存贮器中, n T nT nT 仅代表前后顺序,故信号(或序列)简写为 x ( n ) x(n) x(n)。
- 对具体信号, x ( n ) x(n) x(n) 也代表第n个序列值。
- n n n 取整数,非整数时无定义;而在n时刻序列的取值等于信号的采样值,即 x ( n ) = x a ( n T ) − ∞ < n < + ∞ \begin{aligned} x(n) = x_a(nT) -\infty < n < +\infty \end{aligned} x(n)=xa(nT)−∞<n<+∞
2. 离散时间信号的时域表示
- 枚举法
- 公式 (解析式)法
- 图解法
3. 常用序列
(1)单位采样序列(单位脉冲序列)

- 与
δ
(
t
)
\delta(t)
δ(t)的
区别:模拟信号和系统中的单位冲激函数 δ ( t ) δ(t) δ(t) 在 t = 0 t=0 t=0时取值无穷大, t ≠ 0 t≠0 t=0时取值为零,对时间 t t t的积分为1。 - 单位采样序列作用:用其的移位和加权表示任意的离散时间序列
(2)单位阶跃序列

-
δ
(
n
)
δ(n)
δ(n)与
u
(
n
)
u(n)
u(n)之间的关系:
δ
(
n
)
=
u
(
n
)
−
u
(
n
−
1
)
δ(n) =u(n)-u(n-1)
δ(n)=u(n)−u(n−1)
(差分) - δ ( n ) δ(n) δ(n)与 u ( n ) u(n) u(n)之间的关系: u ( n ) = ∑ k = 0 + ∞ δ ( n − k ) u(n) = \sum_{k=0}^{+\infty}\delta(n-k) u(n)=∑k=0+∞δ(n−k)
(3)矩形序列

(4)实指数序列

(5)正弦序列

- 因为在数值上,序列值与采样信号值相等,因此得到数字频率 ω 与模拟角频率Ω之间的关系为 ω = Ω T ω=ΩT ω=ΩT
- 上式具有普遍意义,它表示凡是由模拟信号采样得到的序列,模拟角频率Ω与序列的数字域频率 ω ω ω 成线性关系。
(6)复指数序列

(7)周期序列
如果对所有n存在一个最小的正整数N,使下面等式成立:
x
(
n
)
=
x
(
n
+
N
)
,
−
∞
<
n
<
∞
\begin{aligned} x(n)=x(n+N), -∞<n<∞ \end{aligned}
x(n)=x(n+N),−∞<n<∞则称序列x(n)为周期性序列,周期为N(N为整数)。
- 对一般的正弦序列而言: x ( n ) = A s i n ( ω 0 n + φ ) x(n)=Asin(ω_0 n+φ) x(n)=Asin(ω0n+φ),如果要求该序列为周期序列,则要求满足: N = 2 π ω 0 k N=\frac{2π}{ω_0}k N=ω02πk。式中k与N均取整数,且k的取值要保证N是最小的正整数。满足这些条件,正弦序列才是以N为周期的周期序列。
- 具体来说正弦序列有以下三种情况:
-
- 当 2 π / ω 0 2π/ω_0 2π/ω0为整数时,k=1,正弦序列是以 2 π / ω 0 2π/ω_0 2π/ω0为周期的周期序列。
-
- 当 2 π / ω 0 2π/ ω_0 2π/ω0不是整数,而是一个有理数。 N = ( 2 π / ω 0 ) k = P / Q ∗ Q = P N= (2π/ω0)k = P/Q*Q=P N=(2π/ω0)k=P/Q∗Q=P,即正弦序列是以 P P P为周期的周期序列。
-
- 如 2 π / ω 0 2π/ω_0 2π/ω0 是无理数,此时的正弦序列不是周期序列
- 正弦信号或复指数信号是周期信号,但正弦序列或复指数序列不一定是周期序列
(4)序列的运算–乘法、加法、移位、翻转及尺度变换
二、离散时间系统
性质:线性或非线性、时变或时不变、因果或非因果、稳定或不稳定

(1)线性系统

(2)时不变系统
如果系统对输入信号的运算关系
T
[
⋅
]
T[·]
T[⋅] 在整个运算过程中不随时间变化,或者说系统对于输入信号的响应与信号加于系统的时间无关,则这种系统称为时不变系统 (理解为:不时变),表示如下:
I
F
:
y
(
n
)
=
T
[
x
(
n
)
]
,且
T
[
x
(
n
−
n
0
)
]
=
y
(
n
−
n
0
)
\begin{aligned} IF: y(n)=T[x(n)],且 T[x(n-n0)] = y(n-n0) \end{aligned}
IF:y(n)=T[x(n)],且T[x(n−n0)]=y(n−n0)
T
H
E
N
:
系统是非时变的!
\begin{aligned} THEN : 系统是非时变的! \end{aligned}
THEN:系统是非时变的!
- 证明方法:分别对 y ( n ) y(n) y(n) 与 T [ x ( n ) ] T[x(n)] T[x(n)] 的自变量进行时延 n 0 n_0 n0,并比较二者是否相同
- 注意: y ( n ) y(n) y(n)的自变量是 n n n, T [ x ( n ) ] T[x(n)] T[x(n)]的自变量是 x ( n ) x(n) x(n)
(3)系统的因果性



(4)系统的稳定性

三、离散系统的描述
1. 线性卷积

- 式中的符号*代表线性卷积运算,*与系统之间存在一一对应的关系;
- 上式表示LTI系统的输出等于输入序列和该系统的单位脉冲响应的卷积;
- 只要知道系统的单位脉冲响应,按照上式,对于任意输入x(n)都可以求出系统的输出。

线性卷积计算的方法:
- 解析方法
- 图解方法
- 不进位乘法
- 矩阵表示方法
- Z变换方法
2. 线性常系数差分方程表示LTI系统
(1)基本概念
描述一个系统,可以不管系统内部的结构如何,将系统看成一个黑盒子,只描述或者研究系统输出和输入之间的关系,这种方法称为输入输出描述法。
- 模拟系统:由
微分方程描述系统输出输入之间关系; - 离散时间系统:用
差分方程描述系统输出输入之间关系; - 线性时不变系统(LTI):用
线性常系数差分方程描述系统输出输入之间关系。

(2)线性常系数差分方程的求解
已知系统的输入序列,通过求解差分方程可以求出输出序列。求解差分方程的基本方法有以下三种:
- 变换域方法:Z变换。
- 时域解法:
-
- 经典解法:闭合形式的解(齐次解加特解),应用少;
-
- 递推解法:数值解;
已知:输入序列和N个初始条件(N为系统阶数)
求解:n时刻的输出,并递推出n+1时刻的输出
结论1:差分方程本身并不能确定该系统是因果还是非因果系统,还需要用初始条件进行限制。(因果性:在n<0 时,没有输入信号,输出只能为零)结论2:线性常系数差分方程描述的系统并不一定是线性时不变系统,这和系统的初始状态有关。
总结:即差分方程本身不能够确定系统的因果性和时不变性。
采用线性常系数差分方程描述系统时,如果没有附加的约束条件,则它不能唯一的确定一个系统的输入和输出关系,也不能保证系统一定是线性时不变系统。
约定:凡用线性常系数差分方程所描述的系统都是指线性时不变系统
四、模拟信号数字处理方法
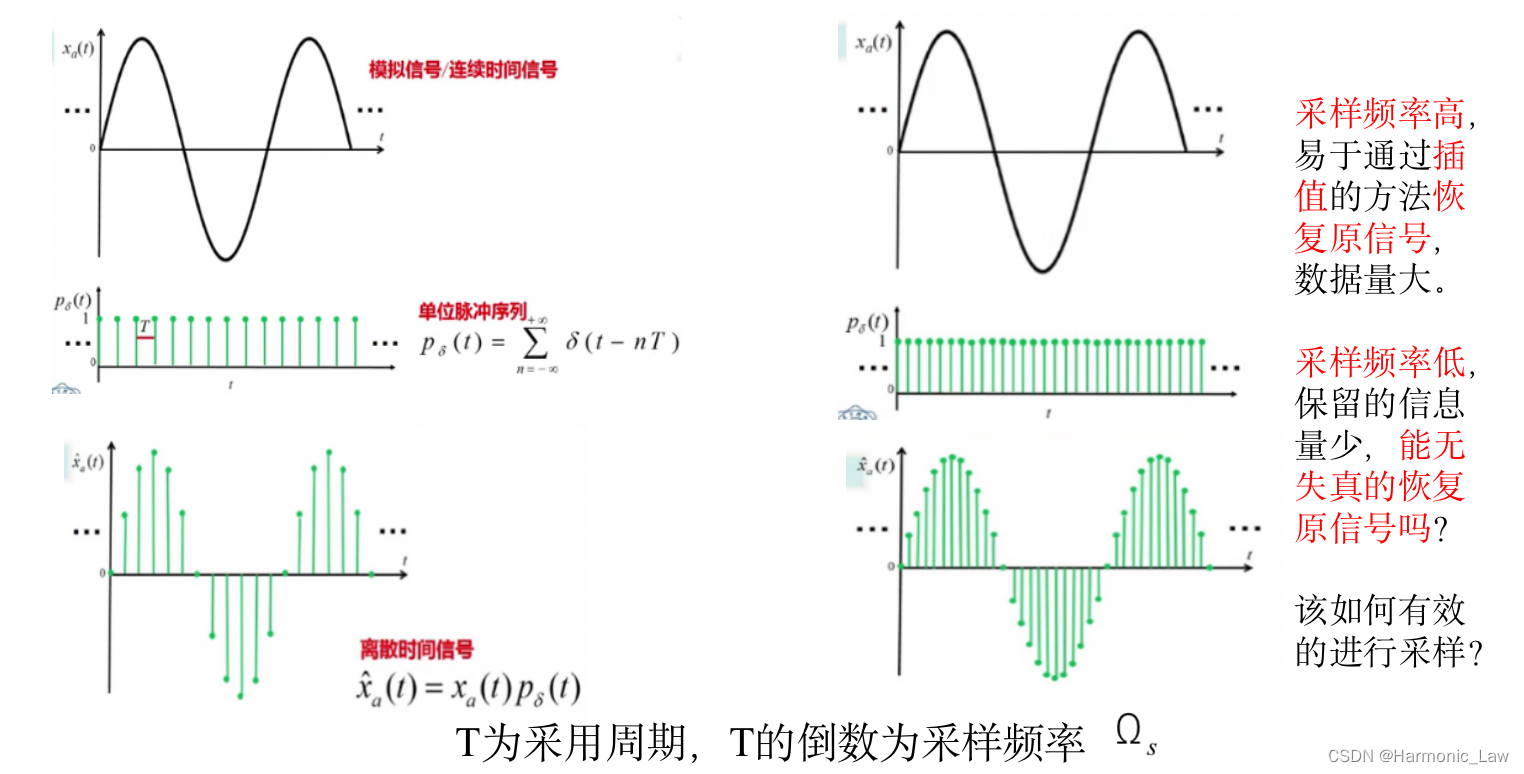


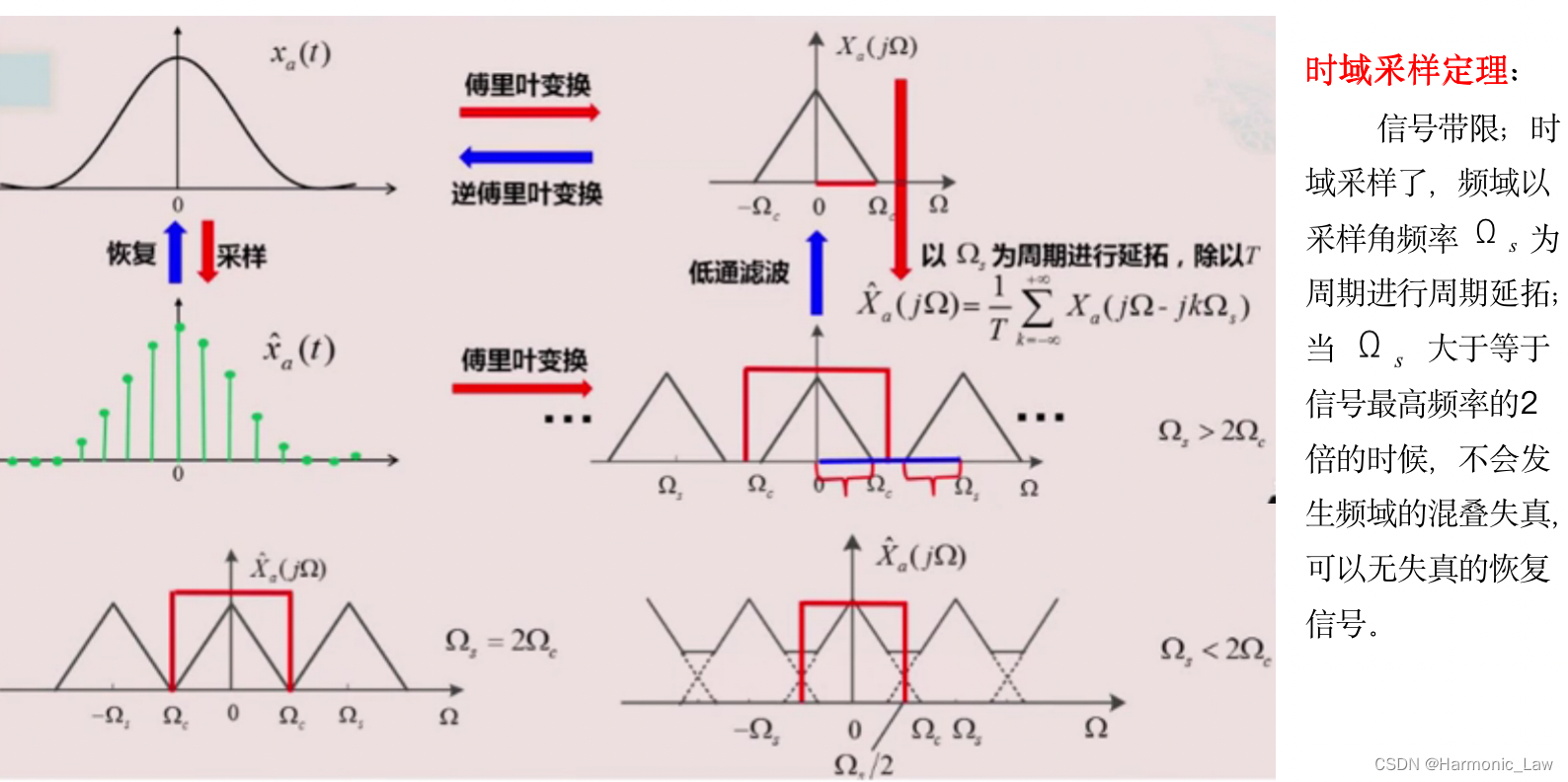







 文章介绍了离散时间信号的基本概念,包括通过等间隔采样模拟信号得到离散序列的过程,以及常见的序列类型如单位采样序列、单位阶跃序列、矩形序列、指数序列和正弦序列。此外,文章还讨论了离散时间系统的性质,如线性、时不变性、因果性和稳定性,并介绍了线性卷积和线性常系数差分方程在描述系统行为中的应用。最后,提到了模拟信号的数字处理方法。
文章介绍了离散时间信号的基本概念,包括通过等间隔采样模拟信号得到离散序列的过程,以及常见的序列类型如单位采样序列、单位阶跃序列、矩形序列、指数序列和正弦序列。此外,文章还讨论了离散时间系统的性质,如线性、时不变性、因果性和稳定性,并介绍了线性卷积和线性常系数差分方程在描述系统行为中的应用。最后,提到了模拟信号的数字处理方法。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








