空间距离（学习笔记）

欧氏距离：（Euclidean distance）是欧几里得空间中两点之间的直线距离。它是最常见和最直观的距离度量方法之一，也是最经常使用的距离度量之一。在二维空间中，欧氏距离可以通过勾股定理来计算，而在更高维度的空间中，它可以推广为：

其中，p和q 是两个向量或数据点，分别表示两个点的坐标，n  表示空间的维度。

简而言之，欧氏距离就是两点之间的直线距离，它基于各个维度上的差异的平方和的平方根来衡量距离。它是一种常用的距离度量方法，因为它易于理解和计算，并且在许多情况下都表现良好。

欧氏距离在许多领域都有广泛的应用，包括机器学习、数据挖掘、图像处理、空间分析等。在机器学习中，欧氏距离通常用作样本之间的相似性度量，例如在 k 近邻算法中，以及在聚类算法中，如 k-means 算法。

曼哈顿距离：（Manhattan distance），也称为城市街区距离或 L1​ 范数，是空间中两点之间的距离，定义为从一个点到另一个点沿着网格线的距离总和，即水平和垂直方向上的距离之和。

在二维空间中，曼哈顿距离可以通过以下公式计算：

其中，p 和 q 分别表示两个点的坐标，∣⋅∣ 表示绝对值。

在更高维度的空间中，曼哈顿距离可以推广为：

其中，n 表示空间的维度。曼哈顿距离得名于纽约曼哈顿的街道网格系统，因为它类似于在城市街区中从一个位置到另一个位置所需的最短行走距离。与欧氏距离不同，曼哈顿距离沿着坐标轴方向的距离是等价的，因此它更适用于那些仅能沿着网格线移动的情况。曼哈顿距离在许多领域都有应用，包括机器学习、路径规划、图像处理等。在机器学习中，曼哈顿距离通常用作距离度量方法之一，特别是在特征空间较稀疏或特征具有明显分布的情况下。例如，在 k 近邻算法中，曼哈顿距离常用作距离度量方法之一。

切比雪夫距离：（Chebyshev distance），也称为棋盘距离或L∞​ 范数，是在几何空间中两个点之间的距离度量，它定义为两点之间各坐标数值差的最大值。因此，切比雪夫距离表示的是在各个坐标轴方向上两点之间的最大距离。

在二维空间中，切比雪夫距离可以通过以下公式计算：

其中，p 和 q 分别表示两个点的坐标。

在更高维度的空间中，切比雪夫距离可以推广为：

其中，n 表示空间的维度。

切比雪夫距离得名于俄罗斯数学家彼得·切比雪夫，因为它与切比雪夫的一些工作有关。切比雪夫距离的特点是考虑了各个坐标轴上的最大距离，因此它可以用来描述两个点之间在各个方向上的最大差异。在一些应用场景中，切比雪夫距离比欧氏距离和曼哈顿距离更为适用，特别是在需要强调最大差异或在各个方向上都有可能的情况下。在机器学习中，切比雪夫距离可以用作距离度量方法之一，例如在聚类算法中或者在图像处理领域中。在某些问题中，切比雪夫距离能够更准确地刻画数据之间的差异，因此在这些问题中可能会选择使用切比雪夫距离作为距离度量方法。

明氏距离（明可夫斯基距离）：用于衡量两个样本之间的相似性。与欧氏距离不同，明氏距离考虑了各个特征之间的相关性，因此在处理具有相关特征的数据时更为适用。

在理解明氏距离之前，先了解协方差矩阵的概念是很重要的。

协方差矩阵：描述了多维数据集中各个维度之间的关系。如果两个特征之间的协方差为正，说明它们具有正相关性，反之为负相关性。协方差的绝对值越大，表示两个特征之间的关联程度越高。

假设有一个包含 n 个特征的数据集，每个特征都有一个均值和标准差。那么，对于数据集中的每个样本向量，可以通过以下方式计算明氏距离：

1. 首先，计算样本向量与数据集的均值向量之间的差异。
2. 然后，将这个差异向量转换为标准化的差异向量，这样每个维度的差异都以标准差为单位进行度量。
3. 最后，利用协方差矩阵对标准化的差异向量进行加权，以考虑不同特征之间的相关性。

明氏距离计算公式：

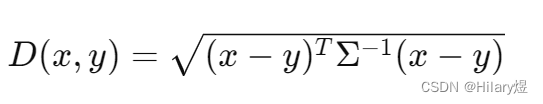
其中，x 和 y 分别表示两个样本向量，ΣΣ 表示数据集的协方差矩阵，Σ−1 表示协方差矩阵的逆。通过计算明氏距离，可以衡量样本之间在多维空间中的相对位置。在许多机器学习算法中，明氏距离被用作相似性度量的一部分，例如在聚类、异常检测和分类等任务。

明氏距离是欧氏空间中的一种测度，被看做欧氏距离和曼哈顿距离的一种推广:P点和Q点之间的明世距离：两点表示为：

距离公式：

p取值为1或2时的明世距离是常用的，p=2即为欧氏距离，p=1则为曼哈顿距离，

当p取正无穷的极限情况下时可以得到切比雪夫距离：

明氏的缺点：

①各个分量的单位必须是等价的，量纲不相等，就无法适用；

②没有考虑各个分量的分布（期望，方差等)可能是不同的，理解为权重；

③各个维度必须是互相独立的，也就是“正交”的。

马氏距离：基于明氏距离的缺点，就诞生了马氏（Mahalanobis）距离，用样本总体协方差解决了所有问题，首先求样本的整体均值，再求样本的协方差矩阵Σ，然后的马氏距离就是,如果协方差是单位或者对角矩阵证明数据之间是正交的，马氏距离就是欧氏距离。

马氏距离的优点：

①它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。

②马氏距离还可以排除变量之间的相关性的干扰。

马氏距离的缺点：

①夸大了变化微小的变量的作用。

②马氏距离并不总是能顺利计算出（满秩方矩阵才可逆，不一定满秩），其次计算过程中，要求总体样本数大于样本的维数（秩<=min(p,n)），否则得不到总体样本协方差矩阵的逆矩阵。协方差矩阵存在不稳定性，虽然得不到的概率很小。

③如果样本的维数非常大，那么计算它的协方差矩阵是十分耗时。