线性回归详解

IT142546355

已于 2022-08-02 19:21:36 修改

阅读量473

点赞数

分类专栏：机器学习文章标签：线性回归 sklearn AI

于 2022-08-02 18:50:22 首次发布

本文链接：https://blog.csdn.net/IT142546355/article/details/126110952

版权

机器学习专栏收录该内容

4 篇文章 0 订阅

订阅专栏

概述

线性回归是机器学习中最基本的回归算法。本文将推导线性回归的MSE损失函数，简单线性回归和梯度下降法拟合线性数据，多项式回归拟合非线性的数据，还将介绍通过正则化的手段防止过拟合，使模型有很强的泛化能力。

MSE损失函数推导

假设随机变量都是相互独立的，依据中心极限定理，其概率分布近似于正态分布，也称高斯分布。在此假定样本误差 $\varepsilon = |y-\hat{y}|$ 都是相互独立的，有上下震荡，震荡是随机变量，当随机变量足够多叠加形成的分布就是正态分布，原始的概率密度函数为：

$f(x|\mu,\sigma^2)=\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

假设有m条样本，令 $\varepsilon_i = |y_i-\hat{y_i}|$ ，其中 $\hat{y_i}=\theta^Tx_i$ ，将 $\varepsilon_i$ 代入，同时可以通过截距项的平移使误差 $\varepsilon$ 的均值 $\mu$ 为0，得：

$f(\varepsilon_i |\mu,\sigma^2)=\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{\varepsilon_i^2}{2\sigma^2}}{\quad},i=1,2,...,m$

依据极大似然估计，总似然函数为：

$\max_\theta L(\varepsilon_1, \varepsilon_2,...,\varepsilon_m) =\prod_{i=1}^mf(\varepsilon_i |\mu,\sigma^2)=\prod_{i=1}^m\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{\varepsilon_i^2}{2\sigma^2}}=\prod_{i=1}^m\frac{1}{\sqrt{2 \pi \sigma^2}}e^{-\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2}}$

对等式两边取对数似然：

$\begin{aligned} l(\theta)&=\max_\theta log\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(\theta^Tx_i-y_i)^2}{2\sigma^2}} \\ &=\max_\theta\sum_{i=1}^{m}log\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(\theta^Tx_i-y_i)^2}{2\sigma^2}} \\ &=\max_\theta[\sum_{i=1}^{m}log\frac{1}{\sqrt{2\pi \sigma^2}}+\sum_{i=1}^{m}loge^{-\frac{(\theta^Tx_i-y_i)^2}{2\sigma^2}}] \\ &=\max_\theta[log\frac{m}{\sqrt{2\pi \sigma^2}}-\frac{1}{2}\cdot \frac{1}{\sigma^2}\sum_{i=1}^{m}(\theta^Tx_i-y_i)^2] \end{aligned}$

去除对求极值无关的项，去除负号极大变极小，最终得MSE损失函数：

$J(\theta)=\min_\theta\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx_i - y_i)^2$

简单线性回归

将运用梯度下降法来一步步的逼近最优解，梯度下降又分为批量梯度下降(BGD)，随机梯度下降(SGD)和微批梯度下降(mini-BGD)，主要的区别是计算梯度时使用的样本的数量，批量梯度下降将所有样本参与梯度的计算，随机梯度下降只使用一条样本参与梯度的计算，微批梯度下降使用的样本数介于前两者之间

对损失函数求 $\theta$ 的梯度：

$\frac{\partial J}{\partial \theta_j}=\sum_{i=1}^{m}(\theta^Tx^i-y^i)x_j^i$

梯度更新：

$\theta_j=\theta_j-\eta \frac{\partial J}{\partial \theta_j}$

模拟梯度下降求解

批量梯度下降

"""
batch gradient descent
批量梯度下降
学习率动态调整
"""
import numpy as np
import matplotlib.pyplot as plt

t0, t1 = 5, 500
def learning_rate_scheduler(t):
    return t0 / (t + t1)

# 超参数
n_iterators = 10000
n_samples = 100
# 数据集
np.random.seed(666)
X = np.random.rand(n_samples, 1)
y = 4 + 3 * X + np.random.randn(n_samples, 1)
X_b = np.c_[np.ones(shape=(n_samples, 1)), X]

# 1,初始化theta，使用正太分布创建
theta = np.random.randn(2, 1)

# 4,判断是否收敛
for idx in range(n_iterators):
    # 2,计算梯度
    gradients = X_b.T.dot(X_b.dot(theta) - y)
    # 3,更新theta
    learning_rate = learning_rate_scheduler(idx)
    theta = theta - learning_rate * gradients

print(theta)
# [[4.02369667]
#  [3.01034894]]

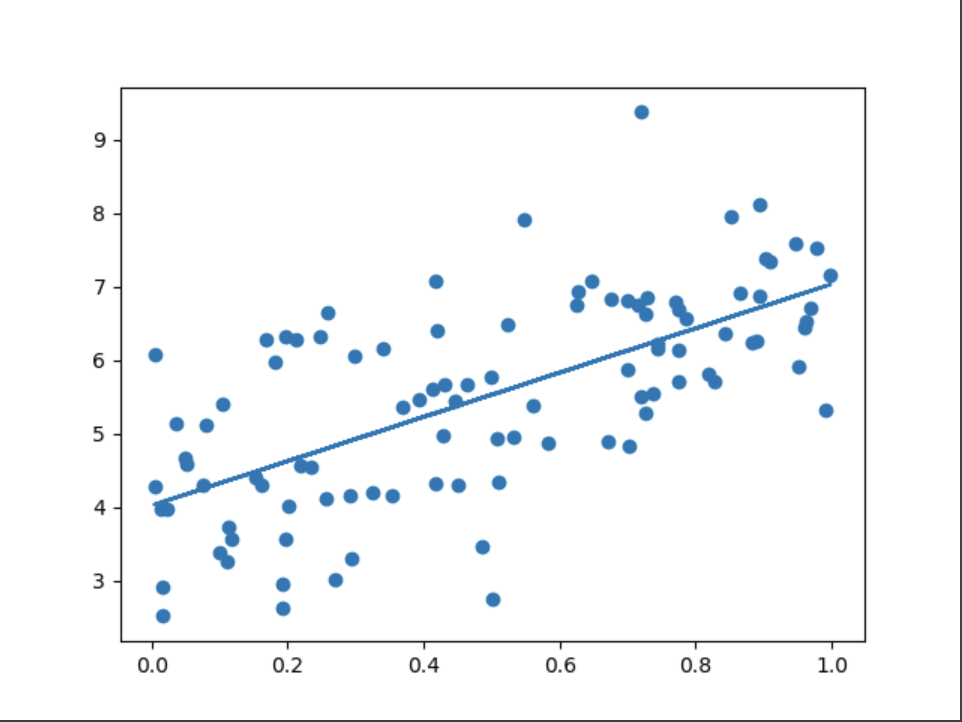
plt.scatter(X, y)
plt.plot(X, X_b.dot(theta))
plt.show()

随机梯度下降

"""
随机梯度下降
stochastic gradient descent
"""

import numpy as np

# 超参数
n_samples = 100
epochs = 10000
learning_rate = 0.001

np.random.seed(666)
X = np.random.rand(n_samples, 1)
y = 4 + 3 * X + np.random.randn(n_samples, 1)
X_b = np.c_[np.ones(shape=(n_samples, 1)), X]

# 初始化theta
theta = np.random.randn(2, 1)

for epoch in range(epochs):
    arr = np.arange(n_samples)
    # 将数据打散
    np.random.shuffle(arr)
    X_b = X_b[arr]
    y = y[arr]
    for idx in range(n_samples):
        x_i = X_b[idx:idx + 1]
        y_i = y[idx:idx + 1]
        # 计算梯度
        gradients = x_i.T.dot(x_i.dot(theta) - y_i)
        # 更新theta
        theta = theta - learning_rate * gradients

print(theta)

微批梯度下降

"""
小批量梯度下降
mini batch gradient descent
"""

import numpy as np

# 超参数
epochs = 10000
learning_rate = 0.001
n_samples = 100
batch_size = 100
num_batch = int(n_samples / batch_size)

# 数据集
np.random.seed(666)
X = np.random.rand(n_samples, 1)
y = 4 + 3 * X + np.random.randn(n_samples, 1)
X_b = np.c_[np.ones(shape=(n_samples, 1)), X]

# 初始话theta
theta = np.random.randn(2, 1)

for epoch in range(epochs):
    # 每个轮次把数据打乱，确保所有数据都能取到
    arr = np.arange(n_samples)
    np.random.shuffle(arr)
    X_b = X_b[arr]
    y = y[arr]
    for idx in range(num_batch):
        x_i = X_b[idx:idx + batch_size]
        y_i = y[idx:idx + batch_size]
        # 计算梯度
        gradients = x_i.T.dot(x_i.dot(theta) - y_i)
        # 更新梯度
        theta = theta - learning_rate * gradients

print(theta)

多项式回归

对于一些数据集通过线性去拟合并不能达到很好的效果，也就是欠拟合。我们可以将原始数据进行升维，将低维的数据映射到高维空间，在高维空间进行线性拟合，从而达到更好的效果，但是不能过分的拟合数据，使模型的泛化能力减弱。增强模型泛化能力的手段就是给目标函数或者损失函数增加惩罚项，这种做法称为正则化，常用的正则化手段有L1正则化和L2正则化，与两者正则化手段相应的的就是Lasso回归和Ridge回归(岭回归)，还有一种结合两种正则化手段的就是ElasticNet(弹性网络)

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
X = 6 * np.random.rand(100, 1) - 3
y = 0.5 * X ** 2 + X + 2 + np.random.randn(100, 1)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

opts = {1: 'g+', 2: 'r.', 10: 'yo'}

# 数据集可视化
plt.scatter(X, y)

for opt in opts:
    # include_bias 已经包含了截距项，故而fit_intercept设置为False
    poly = PolynomialFeatures(degree=opt, include_bias=True)
    X_train_poly = poly.fit_transform(X_train)

    linear_reg = LinearRegression(fit_intercept=False)
    linear_reg.fit(X_train_poly, y_train)

    # 训练集的mse
    y_train_predict = linear_reg.predict(X_train_poly)
    train_mse = mean_squared_error(y_train, y_train_predict)

    # 测试集的mse
    X_test_poly = poly.fit_transform(X_test)
    y_test_predict = linear_reg.predict(X_test_poly)
    test_mse = mean_squared_error(y_test, y_test_predict)

    print("when degree equals {},the train_mse is {} and test_mse is {}".format(opt, train_mse, test_mse))

    plt.plot(X_train_poly[:, 1], y_train_predict, opts[opt], label='degree={}'.format(opt))

plt.legend()
plt.show()

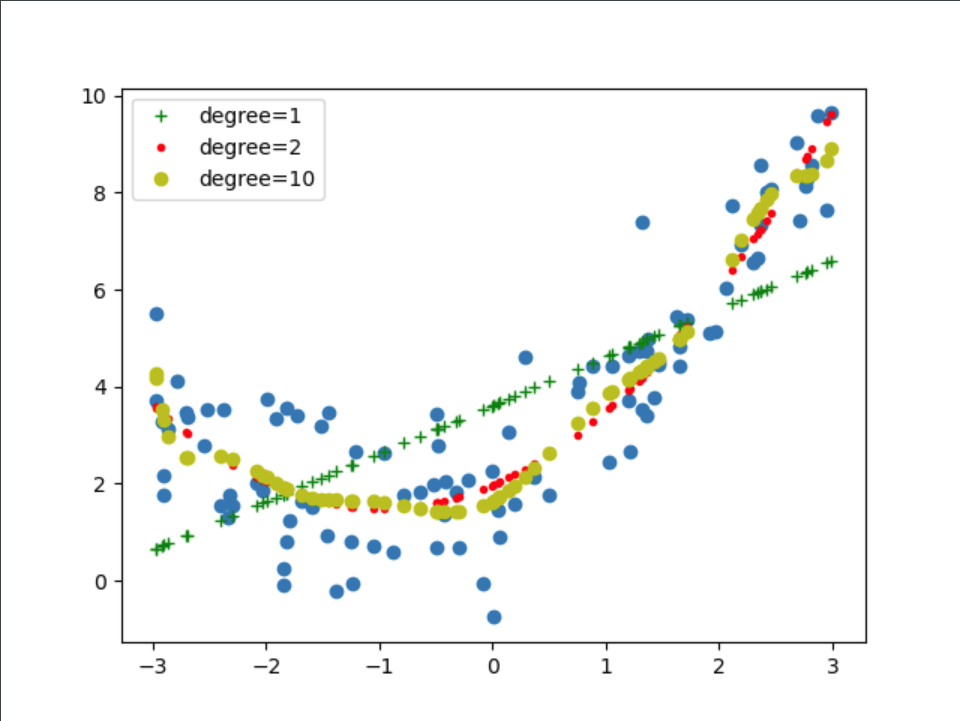
结论：从图和打印的日志可以看出当degree=1的时候，数据拟合的并不好，发生了欠拟合；当degree=2的时候，数据拟合的刚刚好；当degree=10时，数据发生了过拟合，判断的依据是相较于degree=2训练集的MSE损失降低了，但是测试集的MSE损失却升高了

Lasso回归

在损失函数加入L1惩罚项，L1倾向于将一些 $\theta$ 倾向于0， $\lambda$ 是惩罚项因子，来平衡惩罚项和原有的优化项，损失函数如下：

$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx_i-y_i)^2+\lambda\sum_{i=1}^{k}|\theta_i|$

"""
lasso regression
lasso回归
"""

from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor
import numpy as np

np.random.seed(666)
X = np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# lasso_reg = Lasso(alpha=0.01, max_iter=30000)
# lasso_reg.fit(X, y)
# print(lasso_reg.intercept_)
# print(lasso_reg.coef_)

sgd_reg = SGDRegressor(penalty="l1", alpha=0.01, max_iter=30000)
sgd_reg.fit(X, y.reshape(-1,))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)

Ridge回归(岭回归)

在损失函数加入L2惩罚项，L2倾向于将 $\theta$ 整体变小， $\lambda$ 是惩罚项因子，来平衡惩罚项和原有的优化项，损失函数如下：

$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx_i-y_i)^2+\lambda\sum_{i=1}^{k}(\theta_i)^2$

"""
ridge regression
岭回归
"""

from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor
import numpy as np

n_samples = 100

np.random.seed(666)
X = np.random.rand(n_samples, 1)
y = 4 + 3 * X + np.random.randn(n_samples, 1)

# ridge_reg = Ridge(alpha=0.4, solver="sag")
# ridge_reg.fit(X, y)
# print(ridge_reg.intercept_)
# print(ridge_reg.coef_)

sgd_reg = SGDRegressor(penalty="l2", alpha=0.01, max_iter=10000)
sgd_reg.fit(X, y.reshape(-1,))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)

弹性网络

弹性网络结合了L1和L2两种正则化手段，损失函数如下：

$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(\theta^Tx_i-y_i)^2+\alpha p\sum_{i=1}^{k}|\theta_i|+\frac{\alpha(1-p)}{2}\sum_{i=1}^{k}(\theta_i)^2$

"""
elastic regression
弹性网络
"""

from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor
import numpy as np

np.random.seed(666)
X = np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# en_reg = ElasticNet(alpha=0.01, l1_ratio=0.15, max_iter=30000)
# en_reg.fit(X, y)
# print(en_reg.intercept_)
# print(en_reg.coef_)

sgd_reg = SGDRegressor(alpha=0.01, penalty="elasticnet", l1_ratio=0.15, max_iter=1000)
sgd_reg.fit(X, y.ravel())
print(sgd_reg.intercept_)
print(sgd_reg.coef_)

IT142546355

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
线性回归详解

线性回归是机器学习中最基本的回归算法。本文将推导线性回归的MSE损失函数，简单线性回归和梯度下降法拟合线性数据，多项式回归拟合非线性的数据，还将介绍通过正则化的手段防止过拟合，使模型有很强的泛化能力。.........
复制链接

扫一扫