
决定系数(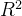 )详解
)详解
决定系数()是回归分析中用于评估模型拟合优度的一个重要统计指标。它表示自变量(特征变量)能够解释因变量(目标变量)变异的程度,取值范围为 [0,1] 或 (−∞,1](取决于模型情况)。在本篇文章中,我们将详细解析
的数学公式、直观理解、计算方法及其在回归分析中的应用。
1. 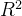 的数学定义
的数学定义
决定系数的公式如下:
其中:
:真实值(True Y)
:模型预测值(Predicted Y)
:真实值的均值(Mean True Y)
:残差平方和(Residual Sum of Squares, RSS),衡量模型预测值与真实值之间的误差。
:总平方和(Total Sum of Squares, TSS),衡量目标变量本身的方差。
(1)分子:残差平方和 RSS
这一项表示模型预测值与真实值之间的误差。误差越大,模型拟合效果越差。
(2)分母:总平方和 TSS
它表示目标变量本身的方差,即目标变量 Y 的离散程度。总平方和衡量的是如果我们用 均值 作为预测值,而不使用任何回归模型时的误差。
(3)决定系数 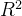 的直观意义
的直观意义
R2R^2R2 可以理解为:
- 模型解释了多少目标变量的变化。如果
,意味着模型可以解释 80% 的目标变量变异。
- 模型的拟合优度。
越接近 1,说明模型的预测能力越强;越接近 0,说明模型几乎没有预测能力。
2. 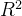 的取值范围及解读
的取值范围及解读
(1)
如果 ,则:
即所有预测值完全等于真实值,说明模型完美拟合数据。但这种情况在现实中极少出现,通常发生在过拟合时。
(2)
如果 ,则:
表示模型预测的误差与直接使用均值预测的误差相同,说明模型没有任何预测能力。
(3)
理论上 不会小于 0,但在某些情况下(如使用不适合的数据或非线性模型时),可能出现
。这表示模型比简单均值预测还要差,说明模型完全不适用于该数据集。
3. 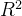 的直观解释
的直观解释
在图中:
- 分子(蓝色部分)表示预测值与真实值之间的误差平方和(RSS)。
- 分母(绿色部分)表示真实值与均值之间的误差平方和(TSS)。
- 公式的意义:
- 当预测误差较小时,RSS 较小,使得
趋近于 1,表示模型较好。
- 当预测误差较大时,RSS 接近或超过 TSS,导致
接近 0 或负值,说明模型较差。
- 当预测误差较小时,RSS 较小,使得
4. 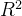 的计算示例
的计算示例
假设我们有以下数据:
| 真实值 | 预测值 |
|---|---|
| 3 | 2.8 |
| 5 | 5.2 |
| 7 | 6.9 |
| 9 | 9.1 |
-
计算均值:
-
计算总平方和 TSS:
-
计算残差平方和 RSS:
-
计算
:
说明模型的拟合效果非常好。
5. 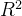 的局限性
的局限性
虽然 是一个重要的评估指标,但它也有一些局限性:
-
不能直接判断模型是否合适
- 高
可能是由于过拟合,即模型学到了训练数据的噪声而不是数据的真实模式。
- 低
并不一定代表模型无效,有时目标变量本身就具有很大随机性。
- 高
-
不能用于非线性关系
主要用于线性回归模型,如果数据具有非线性关系,即使模型有效,R2R^2R2 也可能较低。
-
不能解释因果关系
- 高
仅表明自变量和因变量之间的相关性,但不能说明自变量是否真正导致因变量的变化。
- 高
6. 结论
- 决定系数
衡量模型对目标变量的解释能力,范围通常在 [0,1] 之间。
代表完美拟合,
代表模型无效,
代表模型比随机预测还差。
- 尽管
是重要的评价指标,但在评估回归模型时,应该结合其他指标(如均方误差 MSE、调整
)来全面分析模型性能。
这篇文章结合了数学公式、直观理解、示例计算和实际应用,希望能帮助你深入理解决定系数()!
























 8240
8240

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








