【漫话机器学习系列】190.比值（ODDS）

最新推荐文章于 2025-04-09 09:30:20 发布

IT古董

最新推荐文章于 2025-04-09 09:30:20 发布

阅读量665

点赞数 24

分类专栏：漫话机器学习系列专辑文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/IT_ORACLE/article/details/147041764

版权

漫话机器学习系列专辑专栏收录该内容

277 篇文章

订阅专栏

比值（Odds）详解 —— 理解概率中的另一种表达方式

一、什么是“比值”（Odds）？

在学习概率和统计，特别是在研究分类模型（如逻辑回归）或医学研究（病例对照研究）时，我们经常会遇到“比值”（Odds）这个概念。很多人对“概率”（Probability）比较熟悉，但对“比值”理解不够深入，甚至容易混淆。

其实，比值（Odds）和概率（Probability）是两种不同的表达方式，它们描述的都是某个事件发生的可能性，但视角不一样。

二、从图片内容理解比值的定义

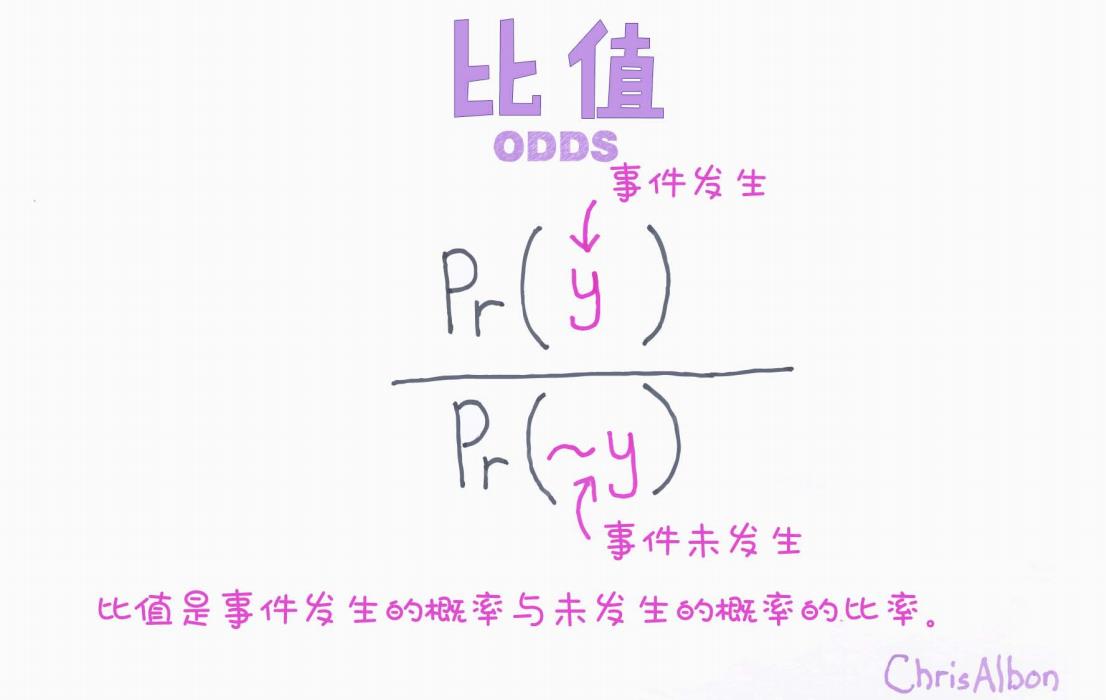
这张图清晰地展示了比值的计算公式和含义：

比值（Odds）的计算公式是：

$\text{Odds} = \frac{\Pr(y)}{\Pr(\neg y)}$

Pr⁡(y)：事件 y 发生的概率
Pr⁡(¬y)：事件 y 不发生的概率（即 1−Pr⁡(y)）

三、图片中的直观说明

“比值是事件发生的概率与未发生的概率的比率。”

也就是说，比值是用来衡量“事件发生”与“事件不发生”之间的相对可能性。

举例说明：

场景	概率	比值
某事件发生的概率是0.75	Pr(y)=0.75 ，Pr⁡(¬y)=0.25	Odds = 0.75 / 0.25 = 3
某事件发生的概率是0.5	Pr(y)=0.5 ，Pr⁡(¬y)=0.5	Odds = 0.5 / 0.5 = 1
某事件发生的概率是0.25	Pr(y)=0.25 ，Pr⁡(¬y)=0.75	Odds = 0.25 / 0.75 ≈ 0.33

四、举个直观的例子

例1：掷硬币

假设正面朝上的概率是 0.5，反面朝上的概率也是 0.5。

那么：

$\text{Odds} = \frac{0.5}{0.5} = 1$

说明：发生和不发生的可能性一样，比值为 1。

例2：掷骰子，掷出 6 的概率

掷出 6 的概率是 1/6，没掷出 6 的概率是 5/6。

所以：

$\text{Odds} = \frac{1/6}{5/6} = \frac{1}{5} = 0.2$

说明：掷出 6 的可能性远小于不掷出 6 的可能性。

例3：某种药物治愈率

结果	概率
治愈	0.8
没治愈	0.2

计算比值：

$\text{Odds} = \frac{0.8}{0.2} = 4$

说明：治愈的可能性是不治愈的 4 倍。

五、比值与概率的区别

概念	定义	取值范围	举例
概率（Probability）	事件发生的可能性	0 到 1 之间	70%的概率是0.7
比值（Odds）	事件发生概率与未发生概率的比率	0 到 ∞	Odds=2表示发生是未发生的2倍可能

六、比值的实际意义

比值 = 1
→ 事件发生和不发生的可能性一样大
比值 > 1
→ 事件更可能发生
比值 < 1
→ 事件更可能不发生

七、比值与胜率（Win Odds）的关系

很多人在博彩、医学、机器学习、Logistic 回归中都会接触到比值。

在医学研究中：
- OR（Odds Ratio，优势比） = 两组比值之比
在Logistic回归中：
- 预测结果是比值的对数（log-odds）

八、比值与概率的互相转换

由概率求比值	由比值求概率
Odds = p / (1-p)	p = Odds / (1 + Odds)

举个例子：

概率p=0.8 → 比值=0.8/0.2=4
比值=4 → 概率=4/(1+4)=0.8

九、总结

核心观点	内容
比值的本质	衡量事件发生与不发生的“强度对比”
和概率的区别	概率关注发生的绝对可能性；比值关注发生与不发生的相对可能性
应用场景	医学、博彩、机器学习、金融、风险评估