目录
6.定义了拉格朗日函数的函数。这个函数用于 SVM 的优化。
9.预测数据的类别,根据 w 和 b 计算预测值,并使用符号函数将连续的预测值转换为类别标签。
6-1支持向量机概述
支持向量机(Support Vector Machines)是一种二分类模型,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,,通俗的来说就是找到一个距离两类数据最远的一个边界,最终转化为一个凸二次规划问题来求解。
间隔最大化,就是所有样本点中,离我们分类界限超平面最近的样本点,尽可能的远离超平面。这种思想在于,不关心远离超平面的样本点,即分类很明确的样本,不作考虑,更关心离超平面近的样本点。这些离超平面较近的点对超平面的位置有着至关重要的影响,抓住这个主要矛盾来分析问题。从个体与整体的角度来看,当两边的离超平面较近的样本点都里超平面足够远时,那么其余的样本点也离超平面足够远。这时,满足间隔最大化的超平面,泛化能力最好。
6-1-1支持向量机实验原理
1.决策边界
,分离超平面。如果数据是线性可分的,这样的超平面有无穷多个,但是间隔最大的分离超平面是唯一的。
所以当时为正类别,反之为负类别
2.支持向量
到决策边界的距离最小的点。SVM核心就是优化决策超平面参数,使支持向量到超平面的距离最大。
如下图中虚线上的向量
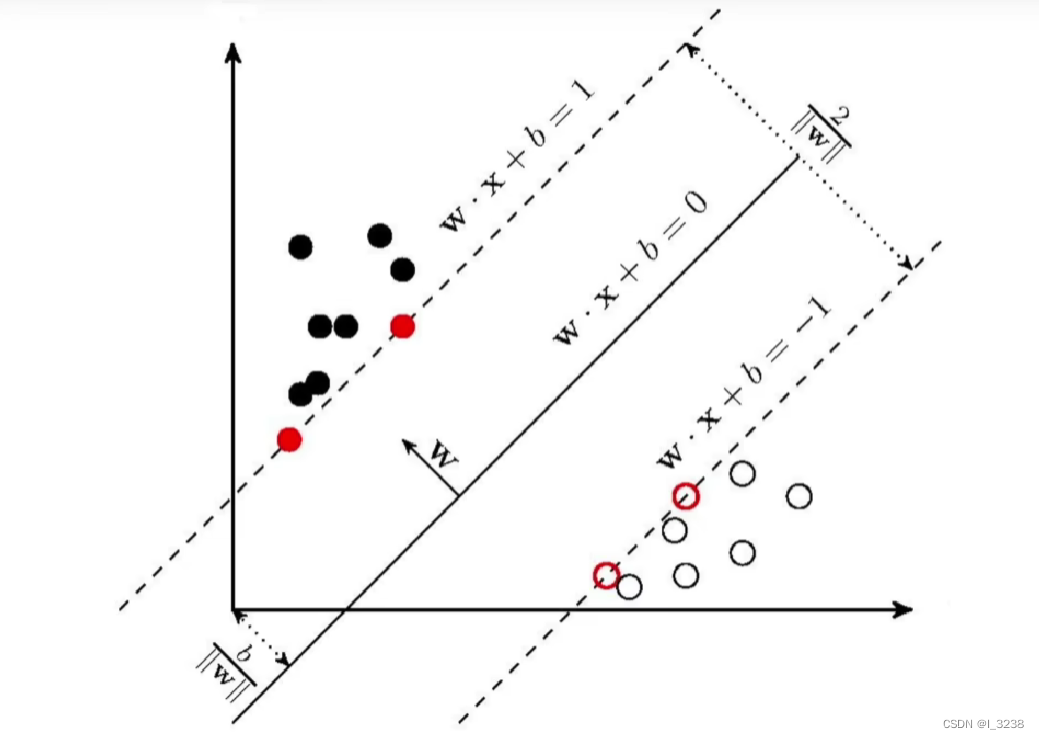
3.几何距离
函数间隔并不能正常反应点到超平面的距离,当分子成比例的增长时,分母也是成倍增长。为了统一度量,我们需要对法向量加上约束条件,这样我们就得到了几何距离
,这个几何间隔在二维空间的理解,就是点到线的距离,几何距离定义为:
其中
4.优化目标
5.约束条件
通过拉格朗日乘子法化为
6.软间隔
实际上,很少有数据集可以完美的符合线性可分的条件,所以要引入软间隔。
引入软间隔后,约束条件从变为
其中
叫做松弛变量。有了松弛变量后,就允许了一些向量可以被错误的分类。
得到软间隔最大化SVM优化函数:
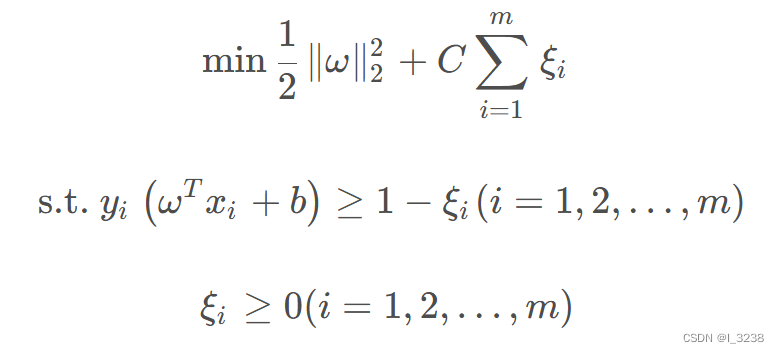
6-2实验代码实现
6-2-1代码步骤
1.设置和数据生成
import numpy as np
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
np.random.seed(12)
num_observations = 502.生成两组服从多变量正态分布的随机数据
x1 = np.random.multivariate_normal([0, 0], [[1, 0.75], [0.75, 1]], num_observations)
x2 = np.random.multivariate_normal([1, 4], [[1.75, 0.75], [0.75, 1]], num_observations)3.将两组数据堆叠在一起,形成一个特征矩阵 x
x = np.vstack((x1, x2)).astype(np.float32)4.生成标签 y
y = np.hstack((np.zeros(num_observations), np.ones(num_observations)))
y = np.where(y <= 0, -1, 1)5.绘制数据的散点图:
plt.figure(figsize=(12, 8))
plt.scatter(x[:, 0], x[:, 1], c=y, alpha=0.4)6.定义了拉格朗日函数的函数。这个函数用于 SVM 的优化。
def Lagrangian(w, alpha, X, y):
first_part = np.sum(alpha)
second_part = np.sum(alpha * alpha * y * y * np.dot(X.T, X))
res = first_part - 0.5 * second_part
return res7.梯度下降算法来优化 SVM 模型的参数 w 和 b。
def gradient_descent(w, b, X, y, lr):
for i in range(2000):
for idx, xi in enumerate(X):
y_i = y[idx]
cond = y_i * (np.dot(xi, w) - b) >= 1
if cond:
w -= lr * 2 * w
else:
w -= lr * (2 * w - np.dot(xi, y_i))
b -= lr * y_i
return w, b8.初始化了 w 和 b,然后通过梯度下降算法来更新它们。
w, b, lr = np.random.random(x.shape[1]), 0, 0.0001
w, b = gradient_descent(w, b, x, y, lr)9.预测数据的类别,根据 w 和 b 计算预测值,并使用符号函数将连续的预测值转换为类别标签。
def predict(X, w, b):
pred = np.dot(X, w) - b
return np.sign(pred)
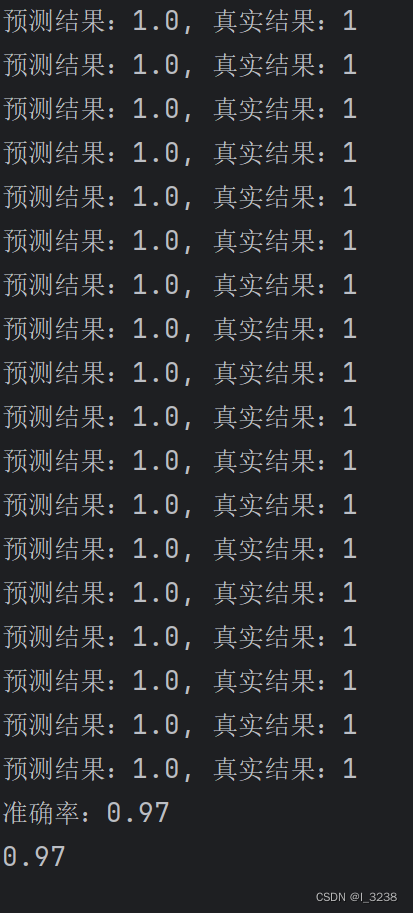
10.计算模型的准确率并打印
svm_pred = predict(x, w, b)
print(accuracy_score(y, svm_pred))输出结果如下:
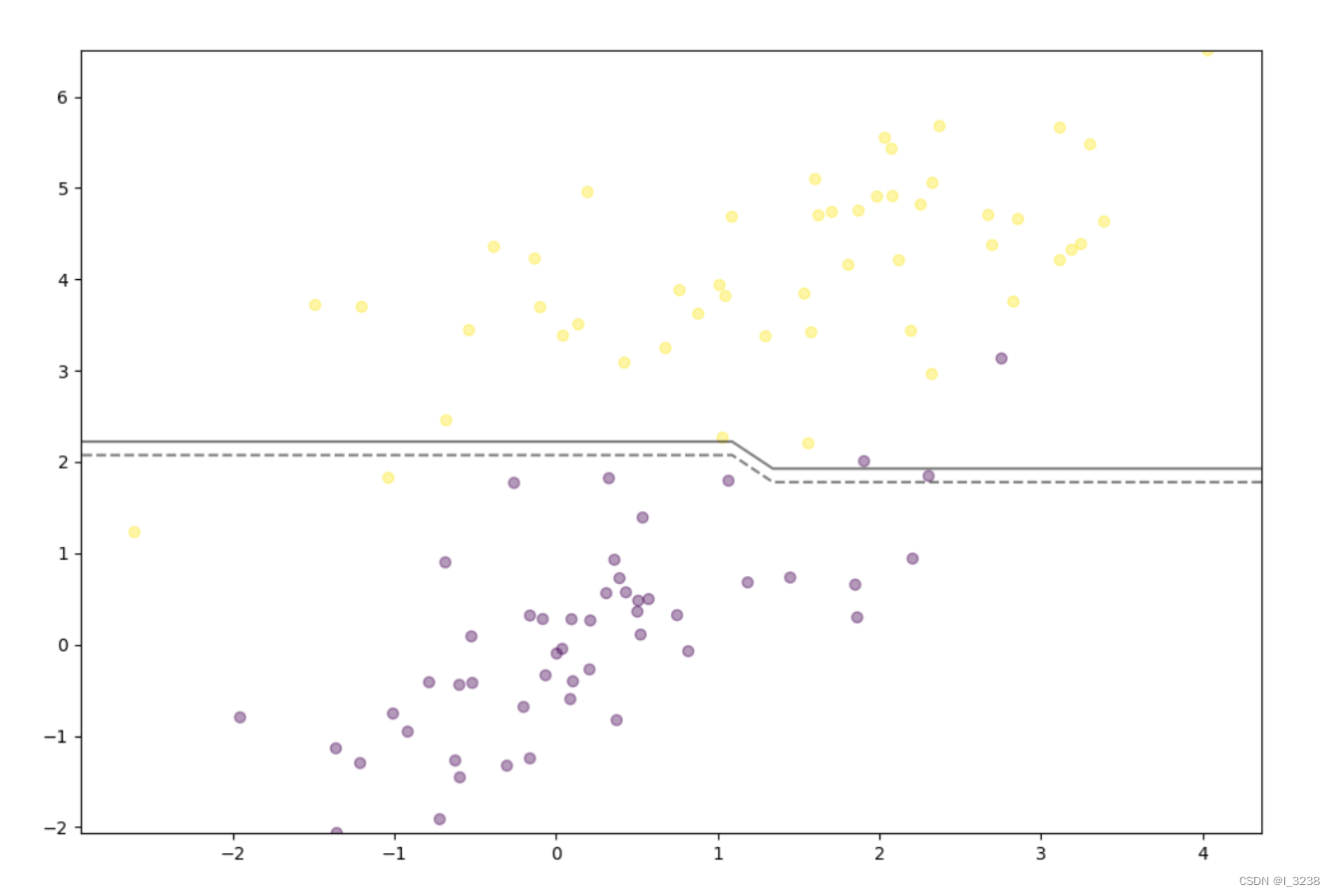
11.绘制决策边界
ax = plt.gca()
xlim = ax.get_xlim()
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(min(x[:, 1]), max(x[:, 1]), 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = np.array([predict(xy, w, b) for xy in xy])
Z = Z.reshape(XX.shape)
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.show()输出结果如下:
6-2-2 总代码
import numpy as np # 导入用于数值计算的库numpy
import seaborn as sns # 导入用于绘制统计图表的库seaborn
import pandas as pd # 导入用于数据处理的库pandas
import matplotlib.pyplot as plt # 导入用于绘图的库matplotlib.pyplot
from sklearn.metrics import accuracy_score # 从sklearn库中导入accuracy_score函数
np.random.seed(12) # 设置随机种子,以便结果可重现
num_observations = 50 # 定义要生成的观测值数量
x1 = np.random.multivariate_normal([0, 0], [[1, 0.75], [0.75, 1]], num_observations) # 生成第一组随机数据
x2 = np.random.multivariate_normal([1, 4], [[1.75, 0.75], [0.75, 1]], num_observations) # 生成第二组随机数据
x = np.vstack((x1, x2)).astype(np.float32) # 将两组数据堆叠在一起,形成特征矩阵x
y = np.hstack((np.zeros(num_observations), np.ones(num_observations))) # 生成标签y,前num_observations个样本标记为0,后num_observations个样本标记为1
y = np.where(y <= 0, -1, 1) # 将类别0的标签转换为-1
plt.figure(figsize=(12, 8)) # 创建画布
plt.scatter(x[:, 0], x[:, 1], c=y, alpha=0.4) # 绘制数据的散点图
def Lagrangian(w, alpha, X, y):
first_part = np.sum(alpha) # 计算拉格朗日函数的第一部分
second_part = np.sum(alpha * alpha * y * y * np.dot(X.T, X)) # 计算拉格朗日函数的第二部分
res = first_part - 0.5 * second_part # 计算最终结果
return res # 返回结果
def gradient_descent(w, b, X, y, lr):
for i in range(2000): # 迭代次数为2000
for idx, xi in enumerate(X): # 遍历特征向量
y_i = y[idx] # 获取当前样本的标签
cond = y_i * (np.dot(xi, w) - b) >= 1 # 计算条件
if cond: # 如果条件成立
w -= lr * 2 * w # 更新权重向量w
else: # 条件不成立
w -= lr * (2 * w - np.dot(xi, y_i)) # 更新权重向量w
b -= lr * y_i # 更新偏置b
return w, b # 返回更新后的权重向量w和偏置b
w, b, lr = np.random.random(x.shape[1]), 0, 0.0001 # 初始化权重向量w、偏置b和学习率lr
w, b = gradient_descent(w, b, x, y, lr) # 使用梯度下降算法更新权重向量w和偏置b
def predict(X, w, b):
pred = np.dot(X, w) - b # 计算预测值
return np.sign(pred) # 使用符号函数将连续的预测值转换为类别标签
svm_pred = predict(x, w, b) # 对数据进行预测
for i in range(len(y)):
print(f"预测结果:{svm_pred[i]}, 真实结果:{y[i]}") # 输出每个测试值的预测结果和真实结果
print(f"准确率:{accuracy_score(y, svm_pred)}") # 计算模型的准确率并打印出来
svm_pred = predict(x, w, b) # 对数据进行预测
print(accuracy_score(y, svm_pred)) # 计算模型的准确率并打印出来
plt.figure(figsize=(12, 8)) # 创建画布
plt.scatter(x[:, 0], x[:, 1], c=y, alpha=0.4) # 绘制数据的散点图
ax = plt.gca() # 获取当前的坐标轴
xlim = ax.get_xlim() # 获取x轴的取值范围
xx = np.linspace(xlim[0], xlim[1], 30) # 在x轴取值范围内生成30个点
yy = np.linspace(min(x[:, 1]), max(x[:, 1]), 30) # 在y轴取值范围内生成30个点
YY, XX = np.meshgrid(yy, xx) # 生成网格点
xy = np.vstack([XX.ravel(), YY.ravel()]).T # 将网格点展开成一组坐标
Z = np.array([predict(xy, w, b) for xy in xy]) # 对网格中的点进行预测
Z = Z.reshape(XX.shape) # 重新塑造预测结果的形状以匹配网格
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--']) # 绘制等高线图作为决策边界
plt.show() # 显示绘制的图形6-3实验结果分析
6-3-1实验中遇到的问题
-
模型复杂度不够: 在这个示例中,我们的模型只有一个线性超平面,这可能不足以很好地分隔具有复杂结构的数据集。在实践中,支持向量机可以使用核函数来实现非线性决策边界,以更好地处理复杂的数据分布。
-
参数调整: 在实际应用中,梯度下降的学习率和迭代次数等参数可能需要仔细调整才能得到良好的结果。
6-3-2实验总结svm支持向量机算法的优缺点
优点:
- 有效处理高维数据:SVM在高维空间中表现良好,适用于特征维度高于样本数的情况,比如文本分类、图像识别等领域。
- 泛化能力强:通过最大化间隔,SVM能够产生能够很好地泛化到新样本的决策边界。
- 鲁棒性:SVM在处理少量训练样本时也能表现良好,不容易受到噪声的影响。
- 核函数:通过核函数,SVM可以将非线性问题映射到高维空间,从而处理非线性可分的数据。
缺点:
- 对大规模数据和高维度数据计算资源消耗大:当数据量很大或者特征维度很高时,SVM的训练时间和内存消耗会很大。
- 选择核函数和参数需要专业知识:在使用核函数时,需要选择合适的核函数及其参数,这需要一定的专业知识和经验。
- 不适合非常不平衡的数据集:对于非常不平衡的数据集,SVM可能会产生偏斜的决策边界,需要特殊处理。
- 不直接给出概率估计:SVM是一个判别式模型,不直接给出样本属于每个类别的概率估计,而是通过间隔来判断样本的类别。





















 1051
1051











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








