动态规划之最长上升子序列问题、最小三角形路径和问题、最小路径和问题（输出最值并打印路径）

最新推荐文章于 2024-07-08 22:12:26 发布

王探赐

最新推荐文章于 2024-07-08 22:12:26 发布

阅读量796

点赞数 19

分类专栏： LeetCode刷题笔记与面试题记录文章标签：动态规划算法

本文链接：https://blog.csdn.net/IntegerList/article/details/139051052

版权

LeetCode刷题笔记与面试题记录专栏收录该内容

1 篇文章 0 订阅

订阅专栏

本篇文章中的几道求最值问题在面试中出现频率较高，就作者本人来说，在面试小红书算法工程师时就碰到了前面两道，当时面试官不仅要求输出最值还要求打印生成最值的路径。因为以往在刷LeetCode时，题目中并没有要求打印形成最值的路径，所以面试时搞得作者一时之间面红耳赤、抓耳挠腮，没有很好的思路…，后经过几天的思考，发现类似的题目最终解题套路其实是很相似的，所以在这篇文章中对以上几道题的解题思路进行了总结和归纳，现和大家进行分享，欢迎讨论。

三道题对应在LeetCode中的编号是：

300. 最长递增子序列（Longest Increasing Subsequence，LIS）

题目：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

输出最值的思路

本题考虑使用动态规划来做，使用动态规划方法需要考虑下面几个问题：

dp数组如何定义？
dp数组如何初始化？
状态转移方程是什么？

dp数组如何定义？

本题中我们可以定义dp数组和原数组长度相同，即len(dp) = len(nums)，都是一维数组，数组中每个元素的值代表对应的nums数组中相同位置处以该元素结尾的最长递增子序列的长度。

dp数组如何初始化？

本题要求的是最长递增子序列，那么最短的子序列会有多长呢？最短的时候就是，每个子序列是其元素本身，即最短子序列的长度为1，那么初始dp数组时就可以这样初始化：dp = [1 * len(nums)]。

状态转移方程是什么？

假设有两个指针j和i，i指针在j指针后面，如果nums[i] > nus[j]，那么dp[i]= max(dp[i], dp[j] + 1)，此时再拿当前最长递增子序列长度max_sub_length和dp[i]进行比较以更新max_sub_length，那么max_sub_length = max(max_sub_length, dp[i])。

根据以上分析不难写出下面的代码：

def lengthOfLIS(self, nums):
  if len(nums) == []:
    return None
  dp = [1] * len(nums)
  max_sub_length = 0
  for i in range(1, len(nums)):
    for j in range(0, i):
      if nums[i] > nums[j]:
        dp[i] = max(dp[i], dp[j] + 1)
    max_sub_length = max(dp[i], max_sub_length)
  return max_sub_length

可以看到代码很简洁，也很容易懂，但是现在再加一个问题，请输出最长子序列长度对应的子序列，比如输出示例1中的数组 [10,9,2,5,3,7,101,18] 对应的最长子序列[2,3,7,101]，现在该如何做呢？

输出最值对应路径的思路

定义一个数组route，记录nums中以每个元素结尾的最长子序列前面一个元素的位置
记录最终最长子序列末尾元素的位置k
根据k和route反推最长子序列中每一个元素的位置
定义一个存储路径结果的数组max_sub_path，其长度等于max_sub_length
额外定义一个指针j，指向max_sub_path中的元素，初始时指向max_sub_path的最后一个元素
反推时从哪开始反推？从最长子序列最后一个元素位置处开始反推

举个例子，还是以[10,9,2,5,3,7,101,18]数组为例，定义一个与其同长的数组route，初始route为route = [0 for _ in range(len(nums))]，即route = [0, 0, 0, 0, 0, 0, 0, 0] ，在通过动归状态转义方程式求最长子序列的过程中，route会逐步的更新为route = [0, 0, 0, 2, 2, 3, 5, 5]，具体地，每个元素对应的以该元素结尾的最长子序列是：

以10结尾的最长子序列是：[10]
以9结尾的最长子序列是：[9]
以2结尾的最长子序列是：[2]
以5结尾的最长子序列是：[2, 5]
以3结尾的最长子序列是：[2, 3]
以7结尾的最长子序列是：[2, 5, 7]或者[2, 3, 7]
以101结尾的最长子序列是：[2, 5, 7, 101]或[2, 3, 7, 101]
以18结尾的最长子序列是：[2, 5, 7, 18]或[2, 3, 7, 18]

至于route中以7结尾的最长子序列前面一个元素为什么记录的是nums[3] = 5而不是nums[4] = 3，是因为此处做了一个假设，即当以某元素结尾的最长子序列存在多个且其长度都一样时，我们只在route[j]处记录第一个以nums[j]元素结尾的最长子序列其倒数第二个元素的位置，即以7结尾时只在route[5]处记录nums[3] = 5这个元素在原数组中的位置。当然非要记录3的位置也行，就看你在同等长度下将最长子序列定义成哪一个了。

此时k会指向元素101，因为此处我选的最长子序列为[2, 5, 7, 101]。

通过route和k倒推最长子序列对应路径的流程如下：

# 先将路径最后一个元素填为最长递增子序列的最后一个元素
j = max_sub_length - 1
max_sub_path[j] = nums[k] 
# 根据route中存储的元素，倒推最长子序列中的每一元素的位置
for i in range(k, -1, -1):
  # 如果route中记录的当前元素和后一个元素相同，只记录后一个元素，否则会重复记录
  if i < k and route[i] == route[i + 1]:
    continue
  j -= 1
  if j < 0:
    # 路径结果集中全存满之后，不再存储
    break
  max_sub_path[j] = nums[route[i]]

倒推的过程模拟如下：

首先，给路径结果集中最后一个元素赋值为101，即max_sub_path[3] = 101
j从后向前移动，j = 2时，max_sub_path[2] = nums[route[6]] =nums[5] = 7
重复执行上个步骤直至max_sub_path填满，在这个过程中要注意一些边界条件及重复值的省略，max_sub_path填满之后直接打断循环。

下面给出上面两个问题合并后的完整代码：

class Solution:
    def length_of_lis(self, nums):
        dp = [1 for _ in range(len(nums))]
        max_sub_length = 1
        k = 0
        route = [0 for _ in range(len(nums))]
        for i in range(1, len(nums)):
            for j in range(i):
            # 此处将初始代码中dp[i] = max(dp[i], dp[j] + 1)，
            # max_sub_length = max(dp[i], max_sub_length)两部分代码分开写了，
            # 目的是记录route和k
                if nums[i] > nums[j]:
                    if dp[j] + 1 > dp[i]:
                        dp[i] = dp[j] + 1
                        # 记录以nums[i]结尾的最长子序列中nums[i]前面一个元素的位置
                        route[i] = j
            if dp[i] > max_sub_length:
                max_sub_length = dp[i]
                # 需要记录最大长度时是以那个元素结尾
                k = i
        print("最长递增子序列长度为：", max_sub_length)
        max_sub_path = [0] * max_sub_length
        j = max_sub_length - 1
        max_sub_path[j] = nums[k]
        for i in range(k, -1, -1):
            if i < k and route[i] == route[i + 1]:
                continue
            j -= 1
            if j < 0:
                break
            max_sub_path[j] = nums[route[i]]
        print("最长递增子序列是：", max_sub_path)

使用如下三个测试用例进行测试：

sl = Solution()
sl.length_of_lis([10, 9, 2, 5, 3, 7, 101, 18])
sl.length_of_lis([0, 1, 0, 3, 2, 3])
sl.length_of_lis([7, 7, 7, 7, 7, 7, 7])

输出为：

最长递增子序列长度为： 4
最长递增子序列是： [2, 5, 7, 101]
**************************************
最长递增子序列长度为： 4
最长递增子序列是： [0, 1, 2, 3]
**************************************
最长递增子序列长度为： 1
最长递增子序列是： [7]

LCR 100. 三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是下标与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

输出最值的思路

和求最长上升子序列一样的，需要考虑动态规划方法的几个基本问题：

dp数组如何定义？

本题定义dp数组形状与原数组相同，数组中每个元素对应的是以原数组中同样位置元素结尾的最小路径和。

dp数组如何初始化？

初始时，即此时没有路径，每个元素都可能是一个路径的起点，那么此时直接将原始数组深拷贝过来：dp = copy.deepcopy(triangle)，其中triangle是原始数组

状态转移方程是什么？

本题从三角形的顶端往下遍历边界条件较多，不如从底端往顶端遍历简单，对于示例1中的三角形：

[
[2],
[3, 4],
[6, 5, 7],
[4, 1, 8, 3]
]

其中dp[2][0]可能的来源有：

dp[2][0] = nums[2][0] + nums[3][0]
或者
dp[2][0] = nums[2][0] + nums[3][1]

那么状态转移公式就可归纳为：

dp[i][j] = min(nums[i][j] + dp[i+1][j], nums[i][j] + dp[i+1][j+1])

根据以上三点，不难写出如下代码：

def minimumTotal(self, triangle: List[List[int]]) -> int:
	n = len(triangle)
  # 浅拷贝时改变dp，triangle里面的元素也会跟着改变，不能浅拷贝！！！
  dp = copy.deepcopy(triangle)
  for i in range(n - 2, -1, -1):
    for j in range(i + 1):
    	dp[i][j] = triangle[i][j] + min(dp[i+1][j], dp[i+1][j+1])

可以看到这代码比上一道题还简洁，有木有？那下面一个问题来了，输出一下最小路径和途径的路径。

输出最值对应路径的思路

定义一个数组route，形状和原数组形状相同，route[i][j]记录的是原数组对应位置处元素triangle[i][j]加上下一行triangle[i+1]中的哪一个元素会形成最小和，可以以元组的形式记录其在triangle中的位置，比如triangle最后一行的元素对应在route中可以是：
```
route[-1][0] = (-1, 0)
route[-1][1] = (-1, 1)
route[-1][1] = (-1, 1)
......
```
route随着dp的记录过程进行填充，上一道题route的填充过程也是一样。
记录最终最小路径和末尾元素的位置k，即(0, 0)，这道题和上面一道题不一样的地方是最终路径都会以三角形顶点元素结尾
根据k和route反推最小路径和途径路径中的每一个元素位置
定义一个存储路径结果的数组min_sum_path，其长度等于triangle的长度
额外定义两个指针row和col存储反推过程中route对应位置处记录的元素位置
反推时从那个位置开始反推？从最小路径和对应的路径最后一个元素处开始反推，这道题最后一个元素是固定的，就是(0, 0)

可以看出输出最值对应路径的思路和上道题基本上一模一样，但是本题涉及到二维数组，所以需要使用两个指针row和col记录反推过程中route对应位置处记录的元素的位置。根据上述思路可以写出如下代码：

min_sum_path = []
min_sum_path.append(triangle[0][0])
row = route[0][0][0]
col = route[0][0][1]
for i in range(1, len(triangle)):
  for j in range(i + 1):
    if i == row and j == col:
      min_sum_path.append(triangle[row][col])
      row = route[i][j][0]
      col = route[i][j][1]

这个过程比上一道题的要清晰不少，也不用考虑什么边界条件。

填充route涉及到的代码：

route = [[0] * len(_) for _ in triangle]
triangle_length = len(triangle)
for i in range(triangle_length - 1, -1, -1):
  for j in range(i + 1):
    # 同样的，此处要对dp[i][j] = min(nums[i][j] + dp[i+1][j], 
    #															nums[i][j] + dp[i+1][j+1])
    # 这行代码细化
    if i == triangle_length - 1:
      route[i][j] = (i, j)
    else:
      sum_1 = triangle_length[i][j] + dp[i + 1][j]
      sum_2 = triangle_length[i][j] + dp[i + 1][j + 1]
      if sum_1 < sum_2:
        dp[i][j] = sum_1
        route[i][j] = (i + 1, j)
      else:
        dp[i][j] = sum_2
        route[i][j] = (i + 1, j + 1)

合并输出最值和最值对应路径的代码如下：

class Solution:
    def minimumTotal(self, triangle):
        dp = copy.deepcopy(triangle)
        triangle_length = len(triangle)
        route = [[0] * len(_) for _ in triangle]
        for i in range(triangle_length - 1, -1, -1):
            for j in range(i + 1):
                # 同样的，此处要对dp[i][j] = min(nums[i][j] + dp[i+1][j],
                #							  nums[i][j] + dp[i+1][j+1])
                # 这行代码细化
                if i == triangle_length - 1:
                    # dp[i][j] = triangle[i][j]
                    route[i][j] = (i, j)
                else:
                    sum_1 = triangle[i][j] + dp[i + 1][j]
                    sum_2 = triangle[i][j] + dp[i + 1][j + 1]
                    if sum_1 < sum_2:
                        dp[i][j] = sum_1
                        route[i][j] = (i + 1, j)
                    else:
                        dp[i][j] = sum_2
                        route[i][j] = (i + 1, j + 1)
        print("最小路径和是：", dp[0][0])
        min_sum_path = []
        min_sum_path.append(triangle[0][0])
        row = route[0][0][0]
        col = route[0][0][1]
        for i in range(1, len(triangle)):
            for j in range(i + 1):
                if i == row and j == col:
                    min_sum_path.append(triangle[row][col])
                    row = route[i][j][0]
                    col = route[i][j][1]
        print("最小路径和对应的路径是：", min_sum_path)

使用如下两个测试用例进行测试：

sl = Solution()
sl.minimumTotal([[2],[3,4],[6,5,7],[4,1,8,3]])
sl.minimumTotal([[-10]])

输出为：

最小路径和是： 11
最小路径和对应的路径是： [2, 3, 5, 1]
**************************************
最小路径和是： -10
最小路径和对应的路径是： [-10]

LCR 099. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

**说明：一个机器人每次只能向下或者向右**移动一步。

示例 1：

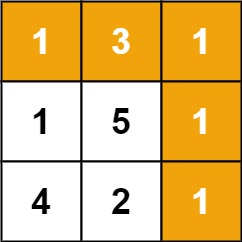
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

输出最值的思路

和前两道题一样，需要考虑动态规划方法的几个基本问题：

dp数组如何定义？

本题定义dp数组形状与原数组相同，dp数组中每个元素对应的是以原数组中同样位置处元素结尾的最小路径和。

dp数组如何初始化？

这道题要注意一点，机器人每次只能向右或者向下移动一步，那么第一行和从左往右数的第一列可以如下初始化：

dp = copy.deepcopy(grid)
for i in range(len(grid)):
  for j in range(len(grid[i])):
    # 第一行，因为第一行的元素对应位置处的最小值只能从第一行左侧的元素得到
    if i == 0 and j > 0:
      dp[i][j] = dp[i][j-1] + grid[i][j]
    # 第一列，因为第一列的元素对应位置处的最小值只能从第一列上侧的元素得到
    if j == 0 and i > 0:
      dp[i][j] = dp[i-1][j] + grid[i][j]

状态转移方程是什么？

dp[i][j]只能从其左侧元素或者上侧元素推导得来，所以有：

dp[i][j] = min(grid[i][j] + dp[i-1][j], grid[i][j] + dp[i][j-1])

那么状态转移公式就可归纳为：

dp[i][j] = min(nums[i][j] + dp[i+1][j], nums[i][j] + dp[i+1][j+1])

则这道题求最小路径和的代码为：

def minPathSum(self, grid: List[List[int]]) -> int:
    dp = copy.deepcopy(grid)
    for i in range(len(grid)):
        for j in range(len(grid[i])):
            if i == 0 and j > 0:
                dp[i][j] = dp[i][j-1] + grid[i][j]
            if j == 0 and i > 0:
                dp[i][j] = dp[i-1][j] + grid[i][j]
    for i in range(1, len(grid)):
        for j in range(1, len(grid[i])):
            dp[i][j] = min(grid[i][j] + dp[i-1][j], grid[i][j] + dp[i][j-1])
    return dp[-1][-1]

输出最值对应路径的思路

和上一道题差不多，主要需要关注的点还是在于：

route如何定义？其中的每一个元素是什么含义？

定义成和原数组一样的形状，初始时其元素值为0。其中每一个元素存储了以当前元素结尾的最短路径其倒数二个元素在原数组中对应的位置。
route如何填充？

随着填充dp数组的过程进行填充
如何根据route倒推路径？

跟三角形最小路径和解法相似，从路径最后一个元素，即grid[-1][-1]开始倒推，设置两个指针row和col记录route[i][j]处存储的以grid[i][j]结尾的路径前一个元素的位置
使用一个新数组min_sum_path存储倒推过程中最小路径和对应路径所历经的元素

route填充代码为：

dp = copy.deepcopy(grid)
route = [[0] * len(grid[0]) for _ in range(len(grid))]
route[0][0] = (0, 0)
for i in range(len(grid)):
  for j in range(len(grid[i])):
    if i == 0 and j > 0:
      dp[i][j] = dp[i][j - 1] + grid[i][j]
      route[i][j] = (i, j - 1)
    if j == 0 and i > 0:
      dp[i][j] = dp[i - 1][j] + grid[i][j]
      route[i][j] = (i - 1, j)
  for i in range(1, len(grid)):
    for j in range(1, len(grid[i])):
      sum_1 = grid[i][j] + dp[i - 1][j]
      sum_2 = grid[i][j] + dp[i][j - 1]
      if sum_1 < sum_2:
        dp[i][j] = grid[i][j] + dp[i - 1][j]
        route[i][j] = (i - 1, j)
      else:
        dp[i][j] = grid[i][j] + dp[i][j - 1]
        route[i][j] = (i, j - 1)

倒推代码为：

min_sum_path = []
min_sum_path.append(grid[-1][-1])
col = route[-1][-1][1]
row = route[-1][-1][0]
for i in range(len(grid) - 1, -1, -1):
  for j in range(len(grid[i]) - 1, -1, -1):
    if i == len(grid) - 1 and j == len(grid[i]) - 1:
      continue
    elif i == row and j == col:
      min_sum_path.append(grid[i][j])
      row = route[i][j][0]
      col = route[i][j][1]

也可以将倒推过程写得更优雅一些：

min_sum_path = []
min_sum_path.append(grid[-1][-1])
row = route[-1][-1][0]
col = route[-1][-1][1]
while col != 0 or row != 0:
  min_sum_path.append(grid[row][col])
  # 可以思考一下为什么会定义new_row和new_col来承接route[row][col][0]
  # 和route[row][col][1]的值
  new_row = route[row][col][0]
  new_col = route[row][col][1]
  row = new_row
  col = new_col
  min_sum_path.append(grid[0][0])
print("最小路径和对应的路径是:", min_sum_path[::-1])

思考：根据上面的这段代码是否可以改进最长递增子序列和三角形最小路径和对应的倒推过程呢？

我不想改进了，交给愿意改进的好兄弟吧！加油ヾ(◍°∇°◍)ﾉﾞ！

合并以上代码：

import copy

class Solution:
    def minPathSum(self, grid):
        dp = copy.deepcopy(grid)
        route = [[0] * len(grid[0]) for _ in range(len(grid))]
        route[0][0] = (0, 0)
        for i in range(len(grid)):
            for j in range(len(grid[i])):
                if i == 0 and j > 0:
                    dp[i][j] = dp[i][j - 1] + grid[i][j]
                    route[i][j] = (i, j - 1)
                if j == 0 and i > 0:
                    dp[i][j] = dp[i - 1][j] + grid[i][j]
                    route[i][j] = (i - 1, j)
        for i in range(1, len(grid)):
            for j in range(1, len(grid[i])):
                sum_1 = grid[i][j] + dp[i - 1][j]
                sum_2 = grid[i][j] + dp[i][j - 1]
                if sum_1 < sum_2:
                    dp[i][j] = grid[i][j] + dp[i - 1][j]
                    route[i][j] = (i - 1, j)
                else:
                    dp[i][j] = grid[i][j] + dp[i][j - 1]
                    route[i][j] = (i, j - 1)
        print("最小路径和是:", dp[-1][-1])
        min_sum_path = []
        min_sum_path.append(grid[-1][-1])
        row = route[-1][-1][0]
        col = route[-1][-1][1]
        while col != 0 or row != 0:
            min_sum_path.append(grid[row][col])
            new_row = route[row][col][0]
            new_col = route[row][col][1]
            row = new_row
            col = new_col
        min_sum_path.append(grid[0][0])
        print("最小路径和对应的路径是:", min_sum_path[::-1])

使用如下两个测试用例进行测试：

sl = Solution()
sl.minPathSum([[1,3,1],[1,5,1],[4,2,1]])
sl.minPathSum([[1,2,3],[4,5,6]])

输出为：

最小路径和是: 7
最小路径和对应的路径是: [1, 3, 1, 1, 1]
*************************************
最小路径和是: 12
最小路径和对应的路径是: [1, 2, 3, 6]

总结

其实三道题做下来，我们会发现最后两道题的代码反而要比第一道题的简洁一些，这是因为：后面两道题的最值路径起点或终点是固定的，比如第二道题终点就是三角形顶点，第三道题起点就是grid[0][0]、终点就是grid[-1][-1]。而第一道题则起点既不固定，终点也不固定，这可能是复原第一道题最值路径的一个难点所在。此外，我还发现复原路径时定义route矩阵，填充route矩阵中值的过程也很像再一次的动态规划过程，不知道大家看完有没有这样的感觉呢？

以上就是本篇文章全部内容，如有错讹，敬请指正！