DeepFool: a simple and accurate method to fool deep neural networks(2016 CVPR)
文章简介:
本文为Adversary Attack方向的一篇经典论文。算法名为DeepFool,其目标是寻求最小的扰动来达到生成对抗样本的目标。下图第2行为DeepFool算法生成的扰动,第3行为FGSM算法生成的扰动。可以看到当生成的target label都为turtle时,DeepFool算法所加入的扰动,明显低于FGSM。DeepFool算法的特点主要为以下几个方面:
- 这是一种untargeted attak
- 该算法是通过寻求当前的点在高维空间中离所有非真实类的决策边界中最近的一个,来作为攻击后的label
- 需要注意的是,该算法是一种贪心算法,并不能保证收敛到(1)中的最优扰动。但是,作者在实践中观察到,该算法产生的扰动非常小,可以认为是最小扰动的很好的近似

Contribute:
- 提出了一种简单、准确的方法来计算比较不对分类器对对抗扰动的鲁棒性

其中 ∇ ( x ; k ^ ) \nabla (x; \hat{k}) ∇(x;k^)为

-
做了广泛的实验比较从而得出
a) 我们的方法比现有的方法更可靠、更有效地计算了对抗性扰动。
b) 发现用对抗性的例子增加训练数据可以显著增强对对抗性扰动的鲁棒性。 -
作者证明,使用不精确的方法来计算对抗性扰动,可能导致对鲁棒性的不同结论,有时还会产生误导。因此,作者的方法提供了一个更好的理解这个有趣的现象及其影响因素。
DeepFool for binary classifiers:
f
f
f是一个线性二分类分类器:
f
(
x
)
=
w
T
x
+
b
f(x)=w^Tx+b
f(x)=wTx+b。如下图,为了使得扰动达到最小,最小的方向就是垂直于分类面的方向。
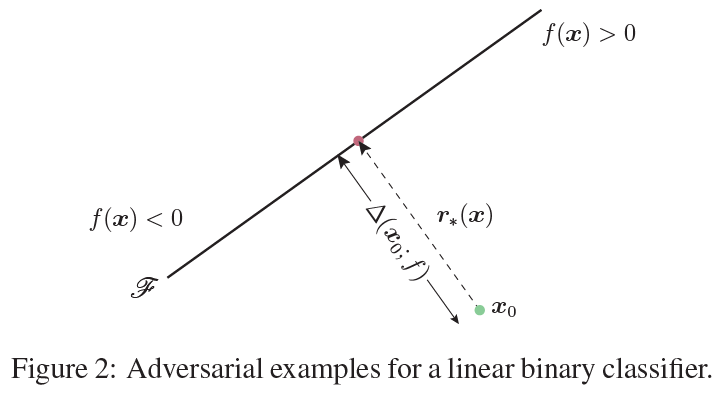


个人感觉这个算法中
r
i
r_i
ri计算结果可能会偏大以至于无法满足题目中最小扰动的目标?
No!
f
(
x
0
)
∣
∣
w
∣
∣
2
2
w
⇒
f
(
x
0
)
∣
∣
w
∣
∣
2
w
∣
∣
w
∣
∣
2
\frac{f(x_0)}{||w||_2^2} w \Rightarrow \frac{f(x_0)}{||w||_2} \frac{w}{||w||_2}
∣∣w∣∣22f(x0)w⇒∣∣w∣∣2f(x0)∣∣w∣∣2w
其中
f
(
x
0
)
∣
∣
w
∣
∣
2
\frac{f(x_0)}{||w||_2}
∣∣w∣∣2f(x0)
为点到平面
f
f
f的距离公式
另外
w
∣
∣
w
∣
∣
2
\frac{w}{||w||_2}
∣∣w∣∣2w
为梯度的单位向量。所以以上就为往梯度方向前进垂直距离大小,即能到达超平面(针对线性超平面而言)。但是事实上神经网络一般都是高度非线性。因此可能未必一次就能到到超平面边界,所以便出现了算法中的while循环。
值得注意的是,算法中为 ∇ f ( x i ) \nabla f(x_i) ∇f(xi)而非 w w w。但是因为 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b,所以 ∇ f ( x i ) = w \nabla f(x_i) = w ∇f(xi)=w。此外,作者发现上述算法通常会收敛到为zero level set中的一个点,因此在实际操作的过程中,作者会将最终的 r ^ \hat{r} r^乘以一个常系数 1 + η 1+\eta 1+η,在作者的实验中,他选取 η = 0.02 \eta=0.02 η=0.02
DeepFool for multiclass classifiers:
- 本文采用的多分类器方案是one-vs-all
- 这里依然考虑的线性分类器
- 分类的结果的选择 k ^ ( x ) = arg max k f k ( x ) \hat{k}(x)= \underset{k}{\arg \max} f_k (x) k^(x)=kargmaxfk(x)其中 f k ( x ) f_k(x) fk(x)是 f ( x ) f(x) f(x)第 k t h k_{th} kth的输出
因此只要在原样本 x 0 x_0 x0上加上扰动 r r r后,满足下式即攻击成功(只要出现某个类的输出置信度高于原类别即满足)

对 k ^ ( x 0 ) = 4 \hat{k}(x_0)=4 k^(x0)=4而言,假设其决策边界为下图,为了用最小的扰动来达到攻击效果,从图中我们可以选择往第3个边界移动。


令
l
^
(
x
0
)
\hat{l}(x_0)
l^(x0)为距离P的边界最近的超平面,其可以通过下式进行计算。有点不明白为什么要通过以下公式计算最近的超平面,而不是直接用点到平面的距离公式?
回答:仔细看超平面的公式为
f
k
(
x
)
−
f
4
(
x
)
=
0
f_k(x) - f_4(x) = 0
fk(x)−f4(x)=0

在计算得出最近的超平面后,我们的扰动可以通过下面的方式进行计算

DeepFool for General classifiers:
- 此时可以是更一般的非线性的分类器

此时P为

上述两种情况都可以归为以下算法

Conclusion:
- 本文提出了一种新的算法DeepFool
- 本文基于分类器的iterative linearization来产生较小的扰动并产生非常有效的攻击效果
- 本文在三个数据集和八个分类器上提供了大量的实验证据,表明了该方法相对于现有的计算对抗性扰动的方法的优越性,以及该方法的有效性。
由于这些笔记是之前整理的,所以可能会参考其他博文的见解,如果引用了您的文章的内容请告知我,我将把引用出处加上~
如果觉得我有地方讲的不好的或者有错误的欢迎给我留言,谢谢大家阅读(点个赞我可是会很开心的哦)~
























 608
608

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








