[文献阅读] A Rough Hypercuboid Approach for Feature Selection in Approximation Spaces

BerryPie1

已于 2024-03-20 00:02:14 修改

阅读量394

点赞数 6

文章标签：机器学习深度学习人工智能

于 2024-03-16 07:49:38 首次发布

本文链接：https://blog.csdn.net/JSDBJSJSH/article/details/136643749

版权

本文提出了一种新的基于粗糙超立方体的特征选择算法，通过最大化相关性、依赖性和重要性，有效处理大量特征数据集。算法利用超立方体等价分区矩阵量化特征的复杂度，实验证明在计算效率和分类准确性上优于传统方法。

摘要由CSDN通过智能技术生成

摘要

选择相关和重要的特征是一个重要问题，尤其是对于具有大量特征的数据集。为此，我们提出了一种基于粗糙超立方体（rough hypercuboid）方法的新特征选择算法。该算法通过最大化所选特征的相关性、依赖性和重要性（relevance, dependency and significance），从数据集中选出一组特征。通过引入超立方体等效分区矩阵（hypercuboid equivalence partition matrix）的概念，提出了一种样本类别对特征依赖程度的新表示方法，用于衡量近似空间（approximation space）中特征的相关性、依赖性和重要性。等效分区矩阵还提供了一种有效的方法来计算更多量化指标，以描述近似分类的不精确性。在粗略超立方体方法的基础上引入了几个定量指标，用于评估所提出方法的性能。在各种不同大小和维度的真实数据集上，广泛证明了所提出的方法在计算复杂性和分类准确性方面优于其他特征选择方法。

相关概念

minimal redundancy-maximal relevance (mRMR) 最小冗余度-最大相关度

一种用于特征选择的算法，目的是识别一组与目标变量相关度最大、且彼此冗余度最低的特征，目的是提高分类器或预测器的性能，同时也减少过拟合和计算复杂性。其中，相关度用特征与目标变量的互信息（mutual information）计算，冗余度用特征之间的互信息计算。

maximal relevance-maximal significance (MRMS) 最大相关度-最大重要度

与mRMR相似，将relevance和significance的标准相结合进行特征选择。mRMR和MRMS都没有考虑高维空间和类别标签的数据分布之间的依赖关系。

rough set 粗糙集

本文中涉及的粗糙集概念已经在粗糙超立方体学习笔记中提到，在此不过多赘述。

hypercuboid 超立方体（将m维数据点集转换为超立方体）

如图1，两种点都有两个特征 $A_i$ 和 $A_j$ ，其中圆点的 $A_i$ 特征的取值范围为 $[A,C]$ ，于是， $[A,C]$ 区间形成了Class A在特征 $A_i$ 维度上的投影，同样地， $[B,D]$ 形成了Class B在特征 $A_i$ 维度上的投影。d维超立方体（d个属性）被定义为其d个正交区间的笛卡尔积。

hypercuboid equivalence partition matrix 超立方体等价划分矩阵

设论域 $U=\{x_1,\dots,x_j,\dots,x_n\}$ ，条件属性集 $C=\{A_1,\dots,A_k,\dots,A_m\}$ ，由决策属性集划分的等价类 $U/D=\{\beta_1,\dots,\beta_i,\dots,\beta_c\}$ 。对于某一条件属性 $A_k$ ，其超立方体等价划分矩阵定义如下：

$H(A_k) = \begin{pmatrix} h_{11}(A_k) & h_{12}(A_k) & \cdots & h_{1n}(A_k) \\ h_{21}(A_k) & h_{22}(A_k) & \cdots & h_{2n}(A_k) \\ \vdots & \vdots & \ddots & \vdots \\ h_{c1}(A_k) & h_{c2}(A_k) & \cdots & h_{cn}(A_k) \\ \end{pmatrix}$

其中 $h_{ij}(A_k)$ 表示第 $j$ 个对象的 $A_k$ 属性是否在等价类 $\beta_i$ 中 $A_k$ 属性的范围内，即区间 $[L_i,U_i]$ 内，形式化的定义为 $h_{ij}(A_k) = \begin{cases} 1, & \text{if } L_i \leq x_j(A_k) \leq U_i \\ 0, & \text{otherwise}. \end{cases}$ 。

这可以看作利用类信息的监督式粒化过程（supervised granulation process）。

决策属性对条件属性或条件属性子集的依赖程度可以通过找到包含误分类对象（misclassified objects）的隐式超立方体来评估。基于超立方体等价分割矩阵的概念，隐式超立方体的误分类对象可以通过如下定义的长度为 $n$ 的混淆向量（confusion vector）来确定： $V(A_k)=[v_1(A_k),\dots,v_j(A_k),\dots,v_n(A_k)]$ ，其中 $v_j(A_k)=min\left \{ 1,\sum_{i=1}^{c}h_{ij}(A_k)-1 \right \}$ ，表示 $x_j$ 是否被包含在超过一个类的边界内。

超立方体等价分割矩阵和 $A_k$ 的混淆向量可用于定义等价类 $\beta_i$ 的上下近似：

$\underline{A}(\beta_i)=\{x_j|h_{ij}(A_k)=1\ and\ v_j(A_k)=0\}$

$\overline{A}(\beta_i)=\{x_j|h_{ij}(A_k)=1\}$

其中 $A$ 是由属性 $A_k$ 引导的等价关系，则 $\beta_i$ 的边界域定义如下：

$BND_A(\beta_i)=\underline{A}(\beta_i)\setminus \overline{A}(\beta_i)=\{x_j|h_{ij}(A_k)=1\ and\ v_j(A_k)=1\}$

dependence and significance 依赖度和重要度

基于粗糙集中上下近似的定义，决策属性 $D$ 的正域、负域和边界域定义如下：

$POS_A(D)=\bigcup_{\beta\in U/D}\underline{A}(\beta_i)$

$NEG_A(D)=U-\bigcup_{\beta\in U/D}\overline{A}(\beta_i)$

$BND_A(D)=\bigcup_{\beta\in U/D}\overline{A}(\beta_i)-\bigcup_{\beta\in U/D}\underline{A}(\beta_i)$

结合前面的超正方体等价划分矩阵和混淆向量的式子，可以得到

$|POS_A(D)|=\sum_{i=1}^{c}\sum_{j=1}^{n}h_{ij}(A_k)\cap[1-v_j(A_k)]$

因此，条件属性 $A_k$ 与决策属性 $D$ 的依赖度可以写为

$\gamma_{A_k}(D)=\frac{1}{n}\sum_{i=1}^{c}\sum_{j=1}^{n}h_{ij}(A_k)\cap[1-v_j(A_k)]=1-\frac{1}{n}\sum_{j=1}^{n}v_j(A_k)$

依赖度是0到1的值，其值越大说明决策属性 $D$ 对条件属性 $A_k$ 的依赖度越高，如果 $\gamma_{A_k}(D)=1$ ，说明 $D$ 完全取决于 $A_k$ 。

若同时考虑多个条件属性，计算其超立方体等价划分矩阵，则有 $H(C)=\bigcap_{A_k\in C}H(A_k)$ ，其中 $h_{ij}(C)=\bigcap_{A_k\in C}h_{ij}(A_k)$ 。同理，同时考虑多个条件属性的混淆向量为 $V(C)=[v_1(C),\dots,v_j(C),\dots,v_n(C)]$ ，其中 $v_j(C)=min\left \{ 1,\sum_{i=1}^{c}h_{ij}(C)-1 \right \}$ ，表示 $x_j$ 的 $C$ 各项条件属性都被包含在超过一个类的边界内。

（接下来是一段有关加速正域计算的式子，由于无法完全理解先放一放...）

结合粗糙集中重要度的定义，以及前面的式子，属性 $A_k$ 关于条件属性集 $C$ 的重要度可以写作 $\sigma_C(D,A_k)=\frac{1}{n}\sum_{j=1}^{n}[v_j(C-{A_k})-v_j(C)]$ ，其值为0到1，其值越高，则属性 $A_k$ 越重要。

算法流程

量化指标

平均准确度（ $\alpha$ 指数）

$\alpha=\frac{1}{c}\sum_{i=1}^{c}\frac{\underline{A}(\beta_i)}{\overline{A}(\beta_i)}$

其中 $|\overline{A}(\beta_i)|=\sum_{j=1}^{n}h_{ij}(S)$ ， $|\underline{A}(\beta_i)|=\sum_{j=1}^{n}h_{ij}(S)\cap[1-v_j(S)]$

$\alpha$ 指数反映了所选择的特征对与决策属性 $D$ 的分辨能力，如果 $\alpha=1$ ，说明决策属性可以由所选择的条件特征集合 $S$ 清晰定义。

平均粗糙度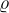（ $\varrho$ 指数）

$\varrho =1-\alpha=1-\frac{1}{c}\sum_{i=1}^{c}\frac{\underline{A}(\beta_i)}{\overline{A}(\beta_i)}$

$\varrho$ 指数表示了所选知识的不完整程度，其值越低，则整体类近似效果越好。

近似准确度（ $\alpha^*$ 指数）

$\alpha^*=\frac{\sum_{i=1}^{c}|\underline{A}(\beta_i)|}{\sum_{i=1}^{c}|\overline{A}(\beta_i)|}$

$\alpha^*$ 指数反应了近似分类的精确度。

近似质量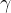（ $\gamma$ 指数）

$\gamma=\frac{1}{|U|}\sum_{i=1}^{c}|\underline{A}(\beta_i)|$

$\gamma$ 指数反映了近似分类算法的质量。

实验结果

以下介绍五个特征评估指数。

Class Separability Index 类分离指数

数据集的类分离指数定义为 $\textit{S}=\textup{trace}(V_B^{-1}V_W)$ ，其中 $V_W$ 是类内散布矩阵（within-class scatter matrix），是在统计模式识别和机器学习中用来量化每个类中的样本围绕其自身类均值的紧密程度的一种度量， $V_B$ 是类间散布矩阵（between-class scatter matrix），衡量的是各类均值围绕所有样本总体均值的散布程度。

Entropy 熵

数据集的熵定义为 $E=-\sum_{i=1}^{n}\sum_{j=1}^{n}S_{ij}\times \textup{log}S_{ij}+(1-S_{ij})\times \textup{log}(1-S_{ij})$ ，其中 $S$ 表示两个体间的相似度，熵能够衡量数据集内部复杂性和无序度。

Representation Entropy 表示熵

表示熵 $H_R$ 是根据数据的特征集的协方差矩阵的特征值来定义的。它通过特征值来量化特征表示中的信息分布，当所有信息都集中在一个方向上时，表示熵达到最小值零；如果所有特征值相等，即所有特征中的信息分布均匀，表示熵则最大。这个度量有助于了解在特征降维过程中涉及的信息和不确定性的多少。

Support Vector Machine 支持向量机

支持向量机（SVM）是一种分类器，它在特征向量空间中寻找一个最优超平面来划分不同类别的样本，旨在最大化类别之间的边界间隔，因而具有良好的泛化能力。SVM的一个关键因素是使用核函数来构造非线性决策边界。在当前的工作中，使用了线性核函数。

C4.5 Decision Tree 决策树

C4.5是基于决策树的分类算法，用于评估缩减特征集对分类效果的影响。它在训练过程中进行特征选择，并且构建的分类模型以决策树的形式表示，可以进一步分析这些树。

SVM和决策树作为分类算法，通过计算分类准确度评估特征选择的表现。

结论

论文的贡献主要有三个方面：

提出了一个融合了粗糙集和超立方体等价划分矩阵优点的特征选择算法；
定义了基于粗糙超立方体描述分类近似性的新的量化指标；
通过在多个现实生活中的数据集上与其他算法的比较，展示了所提算法的有效性。