今天整理一篇关于全同态矩阵乘法优化专题文章,内容包括Cheetah的二维卷积、Iron的矩阵乘法、BumbleBee的矩阵乘法加速、以及最新分享的安全两方隐私推理中的快速同态矩阵向量乘法 Rhombus。
包含以下相关论文:
《Efficient Homomorphic Conversion Between (Ring) LWE Ciphertexts》
《Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference》
《Iron: Private Inference on Transformers》
《BumbleBee: Secure Two-party Inference Framework for Large Transformers》
《Rhombus: Fast Homomorphic Matrix-Vector Multiplication for Secure Two-Party Inference》
CDKS21
该论文提出三种转换方法,包括新的 LWE 密文间密钥切换(Key Switching)操作、LWE 到 RLWE 的转换以及将多个 LWE 密文合并为单个 RLWE 密文的打包算法(PackLWEs),复杂度接近最优且不降低密文级别,可应用于多种场景,如替换旧的 KS 方法、改进混合框架性能等。还提供了实验结果并展示了在安全外包存储和计算方面的应用。
核心思路:包括将或
元素嵌入到
来加速 KS 过程;利用域迹函数将 LWE 转换为 RLWE;采用 FFT 风格的算法打包多个 LWE 密文为单个 RLWE 密文。
转换算法
-
LWE到LWE转换:将LWE密文嵌入
,利用KS算法将密文替换为新密文,从输出密文中提取新的LWE密文,其相位近似保留原相位,该转换复杂度为
。
-
LWE到RLWE转换:通过设置RLWE密文,利用域迹函数
消除无用系数,生成有效RLWE密文,采用递归算法减少转换复杂度,只需
次自同构评估,该算法复杂度为
。
-
LWEs到RLWE转换:将多个LWE密文转换为单个RLWE密文,分打包和迹评估两个阶段,打包算法采用FFT风格合并密文,迹评估消除无用系数,总复杂度为
次同态自同构,当
时,达到渐近最优平均复杂度,可通过预处理步骤去除算法引入的额外项 N。

Cheetah
卷积神经网络隐私推理过程中的方案包含完全基于全同态FHE的方案、基于同态+OT/GC等混合协议的MPC方案。

Cheetah是基于同态+OT/GC等混合协议的MPC方案优化的卷积神经网络隐私推理两方协议,想要完整了解优化要点,可阅读作者之前整理的文章《Cheetah安全多方计算协议-阿里安全双子座实验室》,也可浏览隐语社区视频讲解《Cheetah猎豹及其在隐语中的实现》。

主要技术:
-
优化线性层协议:设计了无需同态旋转和 SIMD 操作的线性层协议,通过特定的编码函数将输入和权重映射到多项式系数,实现高效计算,同时能接受来自的秘密共享输入,提高了效率和灵活性。
-
改进非线性层协议:利用 SlientOT扩展简化和优化非线性函数的计算协议,如提出更精简的百万富翁协议(用于比较整数)和近似截断协议,显著降低了通信成本,同时通过实验验证了近似截断协议在不影响预测结果的前提下提高了效率。
-
其他优化措施:提出减少计算开销的方法,如应用 BN 融合技术节省批量归一化(BN)层和卷积层(CONV)的计算量;通过优化通信过程,减少 Alice 发送的密文数量,降低通信开销。
接下来我们重点来关注一下Cheetah中关于全连接层矩阵-向量乘法的实现细节:
-
Polynomial Coefficient Encoding
图2中展示了全连接层(FC)的安全两方计算(2PC)协议。全连接层中的核心计算是矩阵 - 向量乘法,它可以分解为向量的内积。设计映射函数
和
专门用于使用多项式算术来计算内积。直观地说,当两个N次多项式相乘时,所得多项式的第(N - 1)个系数是两个系数向量按相反顺序的内积。可以轻松地将此想法扩展到一批内积。
为了简单起见,这里首先要求。定义两个映射
和
。

其中 ,
,并且
和
的所有其他系数都设为0。多项式的乘法运算
直接在其某些系数中给出了矩阵 - 向量乘法
的结果
。

当 时,我们可以首先将权重矩阵划分成元素个数为
的子矩阵,使得
。(只要满足该约束条件,
和
就可以作为公共参数自由选取。)当
不是
的整数倍或者
不是
的整数倍时,就会使用零填充。然后,我们将形状为
的矩阵乘法任务转换为规模更小的、形状为
的子任务。
-
2D Convolution

-
Multiplication between a long polynomial and a short polynomial > Convolution

-
High flexibility: stride >= 1 & Same/Valid Padding

-
大矩阵拆分(HWC > N)
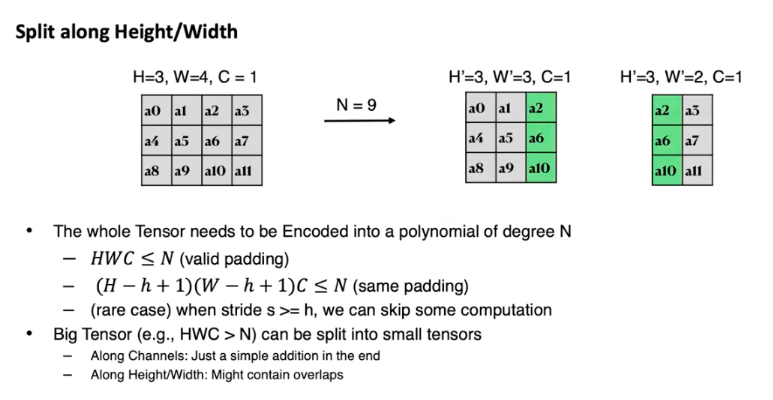
Cheetah中没有使用SIMD,因此不需要p为素数。
Iron

隐私推理旨在保护服务器的模型权重不被客户端获取,同时确保服务器无法得知客户端的私有输入信息。最近,通过使用安全两方计算(2PC)技术[10-14],对传统神经网络(如卷积神经网络)的隐私推理已有研究。然而,由于结构本质上的不同,Transformer模型的隐私推理带来了一些新的挑战。首先,基于Transformer的模型使用大量高维矩阵乘法,而非先前工作中广泛研究的矩阵 - 向量乘法。虽然我们可以直接将先前的矩阵 - 向量乘法协议扩展到我们的设置中,但不幸的是,即使是最有效的设计[14]也会因大量密文交互而产生高额通信开销。其次,基于Transformer的模型在每个模块中使用复杂的数学函数,如Softmax、GELU激活函数[15]和LayerNorm,而非对密码学友好的非线性函数,如ReLU和Maxpool。现有方法要么使用精度受损的高阶多项式近似[16, 11],要么仅在特定场景下支持有限的数学函数[17]。更糟糕的是,所有这些方法计算密集,且通常需要大量通信(更多相关工作,请参考附录A.5)。为了在隐私关键场景中促进基于Transformer的推理服务的广泛采用,为上述复杂操作设计高效协议至关重要。在本文中,我们设计了Iron,一个高效的混合密码框架,用于Transformer模型的隐私推理,不会泄露服务器模型权重或客户端输入的任何敏感信息。Iron为Transformer中的复杂操作贡献了几个新的专门协议,以减轻性能开销。具体来说,我们首先提出一种基于定制同态加密的矩阵乘法协议。我们的思路是通过设计一种紧凑的打包方法,将更多明文输入打包到单个密文中,同时保留矩阵乘法的功能。与Cheetah [14]中实现的最有效的矩阵 - 向量乘法解决方案相比,我们在通信开销方面可以实现
倍(m为输出矩阵的行数)的改进,对于各种Transformer模型,这大约是8倍的降低。其次,我们精心设计了Softmax、GELU和LayerNorm的高效协议。这些协议基于SIRNN [17](用于循环神经网络隐私推理的最先进密码框架)构建,并进行了一些定制优化,例如减少Softmax中的指数运算开销以及简化GELU和LayerNorm。这些优化在三个非线性函数上实现了1.3到1.8倍的运行时减少和1.4到1.8倍的通信减少。此外,这些协议在数值上是精确的,保留了明文模型的准确性。我们还为设计的协议给出了正式的安全证明,以证明其安全保证。基于上述高效组件,我们实现了一个Transformer模型隐私推理框架Iron,并在GLUE基准测试[18]上使用各种BERT架构(BERT - Tiny、BERT - Medium、BERT - Base和BERT - Large)进行了端到端实验。请注意,由于其他基于Transformer的模型(如ViT)具有非常相似的架构和相同的操作,Iron很容易扩展到这些模型。实验结果表明,在四个BERT模型上,Iron相对于SIRNN实现了3到14倍的通信减少和3到11倍的运行时成本降低。此外,与通用的最先进框架MP - SPDZ [16]相比,Iron在通信和计算效率方面都有高达两个数量级的改进。
如上节所示,将经过充分研究的矩阵 - 向量乘法协议[29, 13, 14]简单扩展到我们的矩阵乘法设置中,会导致显著的通信开销,这主要是由于频繁交互密文所致。在这项工作中,我们在最有效的协议Cheetah [14]的基础上构建了一个专门的矩阵乘法协议。回想一下,AHE方案的明文是一个多项式,它可以打包大量输入以分摊开销[29, 13]。我们提出的协议的关键贡献是一种更紧凑的输入打包方法。
符号说明。令
表示x不是y的除数。我们使用粗体小写字母(例如,x)表示向量,使用粗体大写字母(例如,X)表示矩阵。与先前的工作[17, 14]类似,我们使用由Fix表示的定点表示法对输入进行编码(详情请参考附录A.1.1)。令
表示整数多项式的集合,
。我们使用小写字母的上标(例如,
)表示一个多项式,
表示
的第i个系数。给定多项式
,在
上的乘积
定义为
(
公式1)。加法同态加密(AHE)[23, 24]。这种加密方案还能够对密文进行线性同态操作。具体来说,一个AHE方案是一个算法元组AHE =(密钥生成;加密;解密;求值),其参数为
,语法如下:
1)密钥生成
:在输入安全参数 k时,密钥生成是一个随机算法,它输出一个公钥
和一个私钥
。
2)加密
:加密算法Enc取一个明文多项式
,并使用pk将其加密为一个密文多项式
。
3)解密
:在输入sk和一个密文
时,(确定性的)解密算法Dec恢复出明文消息
。
4)求值
:在输入pk、两个包含
、
的密文
、
以及一个线性函数func时,Eval输出一个新的密文
,它加密了
。令 ⊞、⊟、⊠分别表示同态加法、同态减法和与明文的同态乘法。
Iron基于Brakerski-Fan-Vercauteren(BFV)方案[25, 26]构建矩阵乘法协议,BFV方案是基于格的最先进的同态加密解决方案之一。

我们的出发点是,如果我们适当地安排系数,多项式乘法就意味着向量内积[14]。如公式1所示,当两个(N - 1)次多项式相乘时,所得多项式的第(N - 1)个系数是两个系数向量按相反顺序的内积。通过使用适当的系数排列,这个想法可以扩展到矩阵乘法,因为矩阵乘法由一组内积组成。
我们给出两个输入打包函数 和
的定义如下:
,使得对于
,
,
;
,使得对于
,
,
,
其中 和
的所有其他系数都设置为0。多项式乘法
在
的某些系数中直接给出矩阵乘法
的结果。
我们将这个过程形式化如下,并在图2中给出一个简单示例。

定理4.1。假设 ,并且给定两个多项式
和
,矩阵乘法
可以通过乘积
来计算,其中对于
和
,
在
中计算。

我们将证明推迟到附录A.2.1。当时,我们首先将矩阵X、Y分别划分为元素个数为
和
的子矩阵,使得
。当
不能整除
、
不能整除
或
不能整除
时,需要进行零填充。该协议如算法1所示。复杂性和安全性分析。对于复杂性,双方总共交互
个密文,并进行
次同态加法和乘法运算。我们将参数
的选择形式化为一个优化问题,以最小化通信成本。通过我们在附录A.2.2中的分析,
在一般情况下,我们的方法在理论上比Cheetah [14]的通信量提高了倍。值得注意的是,当时,我们将通信成本降低了m倍,因为Cheetah将矩阵的每一行编码为一个密文。此外,安全性证明在附录A.2.3中给出。

该论文提出了用于Transformer 大语言模型的两方私密推理框架 BumbleBee,主要解决了大语言模型在两方设置下的隐私问题。
通过优化矩阵乘法协议和设计高效的激活函数协议,显著提高了计算速度并降低了通信成本。
需要两种类型的矩阵乘法用于Transformer隐私推理:
-
共享矩阵与明文矩阵的乘法(共享输入矩阵与服务器的纯文本权重矩阵之间的乘法)
-
注意力机制内部两个秘密共享矩阵的乘法
Oblivious Linear Transformation (OLT) 的原语
BumbleBee 提出一种名为不经意线性变换(Oblivious Linear Transformation,OLT)的原语来实现这两种类型的矩阵乘法。将OLT描述为一个两方协议,该协议分别从两方获取两个私有矩阵Q和V,并在它们之间生成共享矩阵QV。使用OLT原语,可以通过一次OLT执行来计算共享矩阵 与明文矩阵V之间的乘法。另一方面,对于两个共享矩阵的乘法,需要两次OLT。也就是说,使用两次OLT来计算两个混合项
和
。
现有的基于HE的OLT方法[54]、[36]、[33](OLT,此后称为 KRDY 风格)。KRDY需要两个编码函数 和
,将矩阵编码为可以使用环上带误差学习(RLWE)加密的多项式系数。
与[55]、[62]中使用的其他基于同态加密(HE)的不经意线性变换(OLT)相比,KRDY OLT不需要任何旋转操作(在同态加密中旋转操作非常耗时),因此非常高效。但是,KRDY OLT的结果中有许多“无用”系数。

如图所示:使用 和
的 KRDY计算矩阵乘法的示例。这里 16 个结果系数中有 8 个是“有用的”。
命题1(改编自[54]):假设 。给定两个多项式
,乘法
可以通过环
上的乘积
来计算。即
,对于所有
和
。
根据命题1,在结果多项式 的N个系数中,只有
个系数是“有用”的,但KRDY仍需传输
的整个环上带误差学习(RLWE)密文以进行解密,这可能会造成通信浪费。
例如,考虑一组在Transformer模型中常用的维度,如。在这种情况下,KRDY协议可能需要交换约25MB的密文。由于Transformer模型通常包含数百个这样的大规模矩阵,这可能会产生大量的通信开销。下一节将详细阐述减少这种通信负担的方法。
Ciphertext Packing
BumbleBee首次尝试是将PackLWEs [13]过程应用于KRDY,此后我们将其称为 。PackLWEs过程允许我们从多个RLWE密文中选择任意系数,并通过执行同态自同构将它们组合成单个RLWE密文。在
的情况下,可以将密文数量从
减少到
个密文,代价是
次同态自同构操作。再次考虑矩阵形状
。
现在交换大约2.9MB的密文,这与KRDY的25MB相比有了显著减少。然而,同态加密中的自同构操作相当慢,实际上对于
较大的矩阵,
使用的自同构操作在计算上可能比同态乘法本身更昂贵。
Ciphertext Interleaving
BumbleBee针对矩阵乘法场景中的PackLWEs过程[13]提出了一种专门的优化方法,可以比PackLWEs快近20倍。其主要思路是,不像PackLWEs过程那样逐个“挑选”有用系数,而是更倾向于“清理”结果密文中无用的系数,然后将它们组合成单个密文。
简要描述清理过程。以和
为例。根据定义,自同构操作
得到
,这等价于
在这里,奇数位置系数的符号被翻转。因此,计算将消去奇数索引的系数,并使偶数索引的系数翻倍。更一般地,对于N的任何2的幂次因子,计算
。再次以
为例,我们考虑
。
等于
。
简而言之, 的奇数倍位置的系数符号被翻转。假设对于所有
,
的系数已经为零。那么
将消去
的奇数倍位置的系数,同时使
的偶数倍位置的系数翻倍。我们定义一个函数
,对于
,重复执行公式
r次。执行这些操作后,结果是一个多项式,其中只有
倍数位置的系数不为零。然而,这些系数被缩放了
倍。为了校正这个缩放,我们首先将多项式乘以逆缩放因子
。这隐含地要求一个奇数模数q,这在使用模数
的基于环上带误差学习(RLWE)的同态加密中通常是满足的。此外,ZeroGap过程要求两个所需系数之间的间隔是2的幂次方数。这等于
和
编码中的分区窗口
。请注意,只要满足
,这个分区窗口就可以自由选择。

基于ZeroGap过程的研究,BumbleBee提出了关键贡献,即InterLeave过程。InterLeave过程将个多项式编码成一个多项式,输入系数以
步的跨度排列。首先在图4中给出易于理解的InterLeave版本。在这个简单版本中,分别对每个输入多项式应用ZeroGap过程(步骤2到步骤5)以清理不相关的系数。然后,通过简单的旋转然后求和计算获得最终结果(步骤6到步骤8)。过程中想要强调的是,系数的旋转在密文域中可以比单指令多数据(SIMD)旋转
[32]更高效地实现。实际上,图4计算了次自同构操作,以将N个系数组合成一个多项式。图5给出了一个InterLeave(朴素版)的示例。

BumbleBee现在在图6中展示InterLeave的优化版本,该版本将图4中的复杂度从次自同构操作降低到
。说明此优化版本背后的原理,利用自同构函数的双线性性质,将具有相同索引的两个自同构操作组合成一个自同构操作,从直观上看是合理的。也就是说,对于任何有效的索引g,两个自同构操作
的和等于对和多项式进行的自同构操作。然而,在求和步骤(即图4的步骤8)之前,应用相同自同构索引的多项式会向右移动不同的单位(即图4的步骤6)。为了解决这个问题,我们利用以下等式。即当对于所有满足
的位置i,
时,
等于
。回想一下,操作
会翻转位于
奇数倍位置的系数的符号,而保持位于
偶数倍位置的系数不变。通过乘以
对
进行右移操作,只是简单地改变了
系数位置的奇偶性 —— 从
的奇数倍位置移动到偶数倍位置,反之亦然。因此,先自同构后移位的模式
等同于先取负移位后自同构的模式
。然后,我们可以利用双线性性质将具有相同索引的两个自同构操作组合成一个自同构操作。

[54] P. K. Mishra, D. Rathee, D. H. Duong, and M. Yasuda, “Fast secure matrix multiplications over ring-based homomorphic encryption,” Inf. Secur. J. A Glob. Perspect., vol. 30, no. 4, pp. 219–234, 2021.
[36] Z. Huang, W. Lu, C. Hong, and J. Ding, “Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference,” USENIX Security, 2022.
[33] M. Hao, H. Li, H. Chen, P. Xing, G. Xu, and T. Zhang, “Iron: Private Inference on Transformers,” in NeurIPS, 2022.
[55] P. Mishra, R. Lehmkuhl, A. Srinivasan, W. Zheng, and R. A. Popa, “DELPHI: A cryptographic inference service for neural networks,” in USENIX Security, 2020, pp. 2505–2522.
[62] D. Rathee, M. Rathee, N. Kumar, N. Chandran, D. Gupta, A. Rastogi, and R. Sharma, “CrypTFlow2: Practical 2-party secure inference,” in CCS, 2020, pp. 325–342.
[13] ——, “Efficient Homomorphic Conversion Between (Ring) LWE Ciphertexts,” in ACNS, 2021, pp. 460–479.
[32] S. Halevi and V. Shoup, “Algorithms in HElib,” in CRYPTO, 2014, pp. 554–571.
Rhombus
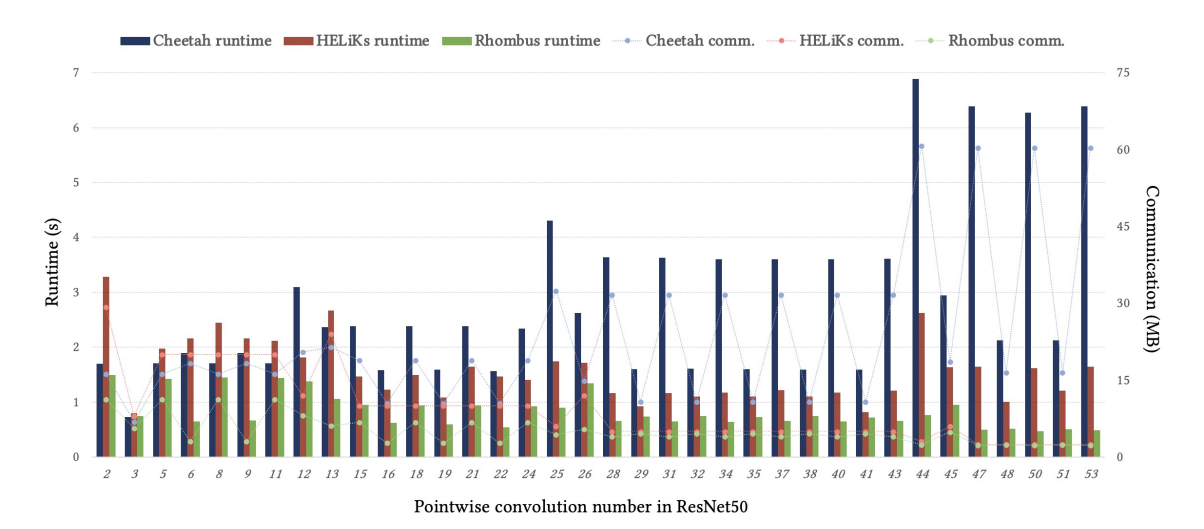
在论文“Rhombus: Fast Homomorphic Matrix-Vector Multiplication for Secure Two-Party Inference”中,作者提出了一种新的安全矩阵-向量乘法(MVM)协议,专为半诚实的两方设置设计。该协议可以无缝集成到现有的隐私保护机器学习框架中,并作为线性层安全计算的基础。Rhombus通过采用基于环学习有噪声加密(RLWE)的同态加密和一系列高效技术,大幅提高了计算性能,相比最新的HELiKs协议,整体性能提升了7.4倍至8倍,ResNet50的安全推理性能提升了4.6倍至18倍。感兴趣的同学可以浏览隐语社区视频讲解 《安全两方隐私推理中的快速同态矩阵向量乘法》。
HELiKs:HE Linear Algebra Kernels for Secure InferenceHELiKs是一种开创性的框架,用于快速安全的矩阵乘法和3D卷积,专为隐私保护机器学习而设计。利用同态加密(HE)和加性秘密共享,HELiKs能够实现安全的矩阵和向量计算,同时确保所有各方的端到端数据隐私。所提出框架的关键创新包括一个有效的乘积累加(MAC)设计,该设计显著降低了HE误差增长,一个部分和累加策略,该策略将HE旋转次数减少了一个对数因子,以及一个新颖的矩阵编码,该编码促进了更快的在线HE乘法,并具有一次性预计算。此外,HELiKs大大减少了用于HE计算的密钥数量,从而在设置阶段降低了带宽使用率。在论文的评估中,HELiKs在运行时间和通信开销方面比现有的安全计算方法显示出相当大的性能改进。通过工作量证明实现(可在GitHub上获得:https://github.com/shashankballa/HELiKs),展示了最先进的性能,与现有技术相比,矩阵乘法的加速倍数高达32倍,3D卷积的加速倍数高达27倍。与现有技术相比,HELiKs还降低了矩阵乘法的通信开销1.5倍,3D卷积的通信开销29倍,从而提高了数据传输的效率。
以上是HELiKs该论文的大致介绍,采用的是NTT编码,具体细节不再展开,有兴趣的同学可以阅读论文细品。
论文链接:https://doi.org/10.1145/3576915.3623136
作者在论文中提出的新的安全矩阵-向量乘法(MVM)协议名为Rhombus,该协议的核心是利用基于环学习有噪声加密(RLWE)的同态加密,结合输入输出打包技术和分裂点选择技术,来显著提高计算效率。
主要创新点包括:
-
输入输出打包技术:该技术通过减少同态加密引起的通信开销,提升了计算效率。论文指出,这种方法能够将通信成本降低约21倍。
-
分裂点选择技术(Split-Point Picking, SPP):该技术允许在计算过程中优化旋转调用的次数,将其降低到与矩阵维度的子线性关系。这意味着在执行复杂的同态运算时,所需的旋转次数显著减少,从而提高了整体性能。
-
高效的矩阵编码方法:Rhombus 引入了新的矩阵编码方法 V1 和 V2,分别针对列和行的打包,进一步提高了通信效率。
-
现有协议的比较:与最近的HELiKs协议相比,Rhombus在MVM协议的整体性能上提升了7.4倍至8倍,并在ResNet50的安全两方推断的端到端性能上提高4.6倍至18倍。


该论文主要是基于HE-MPC hybrid框架下对线性层协议的改进。

同态计算中的两种操作:HomMulPt、HomAut 自同构 (系数编码) / Rotation 旋转 (NTT编码) - 循环移位

CHAM(DAC'23)

PackRLWEs
相比CHAM(DAC'23)的操作(用HomAut操作替换Enc操作),减少了PackLWEs的操作次数,从而减少了HomAut的次数。
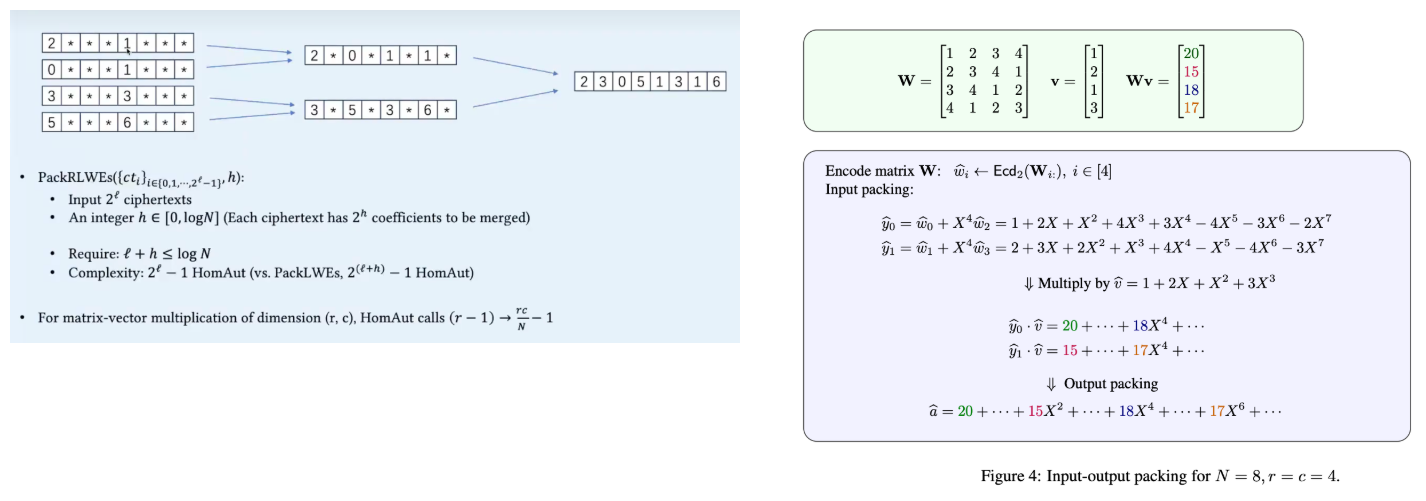
SPP(Split-point picking)

SPP可以再次减少自同构的次数,复杂度由

性能对比






























 598
598

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








