m序列的产生原理及其性质

1 LFSR

        1.1 定义

                线性反馈移位寄存器（LFSR，linear feedback shift register）由n个移位寄存器和若干个异或门组成（各个反馈系数路径只由模二加/异或组成为线性反馈），如下图所示。n级移位寄存器共有2^n个状态，除去全0状态外还剩种状态，故一个n级线性反馈移位寄存器产生的最长周期为。 

                        

                        LFSR有2种形式，分别为异或门内/外接LFSR，如下图。其中，有n级移位寄存器（~），有n+1个反馈系数（~，只能取值0或1，取0/1分别表示反馈通路不存在/存在）。

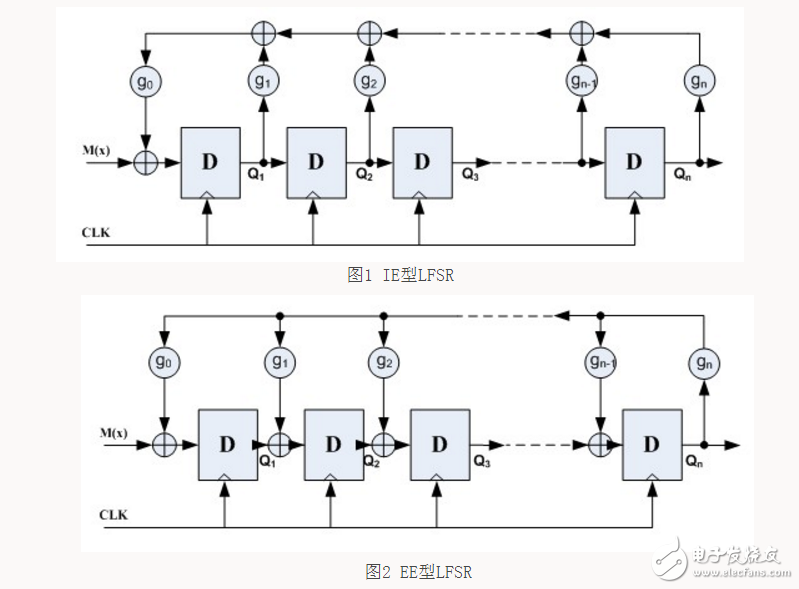
                LFSR的对应的特征多项式为：，其中x的次幂表示元素的对应位置（表示没有寄存器）。   

         1.2 特性 

                对于LFSR有几个特性：

                        ①初始状态（种子SEED）相同，输出序列相同；

                        ②输出序列看起来是随机的（伪随机序列），但达到一定位数后会循环；

                        ③LFSR可以产生的最长的随机序列是长度（即m序列），其中n表示寄存器的数目。

2 m序列

        伪随机（或伪噪声，Pseudorandom Noise，PN）码序列是一种常用的地址码，是一具有与白噪声类似的自相关性质的0和1所构成的编码序列。m序列属于PN码的一种。

        2.1 定义

                m序列是最长线性反馈移位寄存器序列的简称。

        2.2 m序列的产生

                一个LFSR能否产生m序列（最长线性移位寄存器序列），决定于反馈系数（i=0,1,2,...,n），下表列出了部分m序列的反馈系数，其中必有。

                n级线性反馈移位寄存器产生m序列（P=2n-1[m序列的周期]）的充要条件：移位寄存器的特征多项式F(x)为本原多项式。

                当F(x)为n次本原多项式，就一定能产生m序列，满足以下三个条件：

                        ①F(x)是不可约的，即不能再分解多项式；

                        ②F(x)可整除xp+1，这里p=2n-1；

                        ③F(x)不能整除xq+1，这里q<p.

其他m序列的相关知识见m序列产生原理及其性质。