2301: [HAOI2011]Problem b
Time Limit: 50 Sec Memory Limit: 256 MBSubmit: 5322 Solved: 2459
[ Submit][ Status][ Discuss]
Description
Input
第一行一个整数n,接下来n行每行五个整数,分别表示a、b、c、d、k
Output
共n行,每行一个整数表示满足要求的数对(x,y)的个数
Sample Input
Sample Output
和bzoj 1101一模一样的两道题,只不过x和y的范围不是从1开始的而已
理论容斥下就好了
bzoj 1101题解:http://blog.csdn.net/jaihk662/article/details/76392853
但1101题是用莫比乌斯函数+推论解决的
这里尝试用莫比乌斯反演解决,先拉出公式
其实这个公式有另一个表示形式
因为n固定,所以d表示为所有n的倍数(对的,是无穷无尽的,只不过F(d)可能在d超过某个数之后恒为0)
那么这题我们可以
令f(k)为在1<=x<=n, 1<=x<=m且Gcd(x, y)==k的(x, y)对数(也就是答案)
令F(k)为在1<=x<=n, 1<=x<=m且k是Gcd(x, y)的约数的(x, y)对数
那么很显然有
套入莫比乌斯反演公式可得
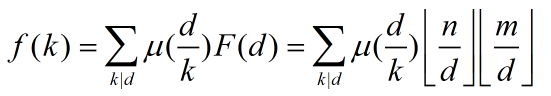
很显然我们只需要枚举小于等于min(n, m)的k的倍数就可以了
到这里说:题目和1101题一模一样,为什么公式不一样?
其实是一样的!对于这公式我们枚举的d是k的倍数,既然这样!那我们假设d = k*d'
那么原式有
转化成功!(注意这里和1101一样我们假设min(n, m)=n)
这样我们原本枚举的小于等于min(n, m)的k的倍数就等同于枚举小于等于min(n, m)的k的倍数再除以k
也就是枚举1到min(n, m)了!
用莫比乌斯反演转化成功
剩下就是和1101一样的两个程序了
#include<stdio.h>
#include<algorithm>
using namespace std;
int cnt, mu[50005] = {1,1}, flag[50005] = {1,1}, pri[50005], sum[50005];
int Jud(int n, int m)
{
int L, R, ans;
ans = 0;
if(n>m) swap(n, m);
L = 1;
while(L<=n)
{
R = min(n/(n/L), m/(m/L));
ans += (sum[R]-sum[L-1])*(n/L)*(m/L);
L = R+1;
}
return ans;
}
int main(void)
{
int i, j, T, a, b, c, d, k;
for(i=2;i<=50000;i++)
{
if(flag[i]==0)
{
pri[++cnt] = i;
mu[i] = -1;
}
for(j=1;j<=cnt&&i*pri[j]<=50000;j++)
{
flag[i*pri[j]] = 1;
if(i%pri[j]==0)
{
mu[i*pri[j]] = 0;
break;
}
mu[i*pri[j]] = -mu[i];
}
}
for(i=1;i<=50000;i++)
sum[i] = sum[i-1]+mu[i];
scanf("%d", &T);
while(T--)
{
scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
printf("%d\n", Jud(b/k, d/k)+Jud((a-1)/k, (c-1)/k)-Jud(b/k, (c-1)/k)-Jud((a-1)/k, d/k));
}
return 0;
}










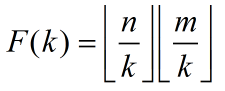
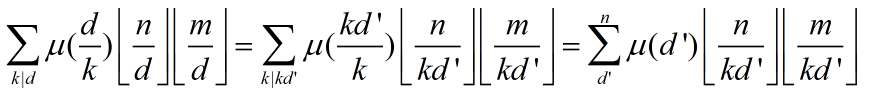














 368
368











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








