臭皮匠与诸葛亮2：1B参数的语言模型能超越405B模型吗？

最新推荐文章于 2025-05-02 12:10:54 发布

庞德公

最新推荐文章于 2025-05-02 12:10:54 发布

阅读量795

点赞数 23

分类专栏：精品论文文章标签：语言模型 TTS 大模型自然语言处理

本文链接：https://blog.csdn.net/Janexjy/article/details/147644116

版权

精品论文专栏收录该内容

40 篇文章

订阅专栏

--->更多内容，请移步“鲁班秘笈”！！<---

Test-Time Scaling，TTS是一种在推理过程中利用额外计算资源来提升大语言模型（LLMs）性能重要方法。TTS在模型测试/推理阶段，采用灵活的策略来优化模型的推理效果或效率的方法。也就是说，当模型训练好之后，在不改模型参数的前提下，通过设计一些推理阶段的策略，来提升模型的表现、控制计算开销，或者兼顾二者。

小编考虑再三，还是将TTS翻译为推理阶段扩展（毕竟测试阶段也是在推理阶段范畴）

其主要核心是将推理扩展策略（Test-Time Strategy，TTS）与过程奖励机制（Process Reward Model, PRM）相结合。

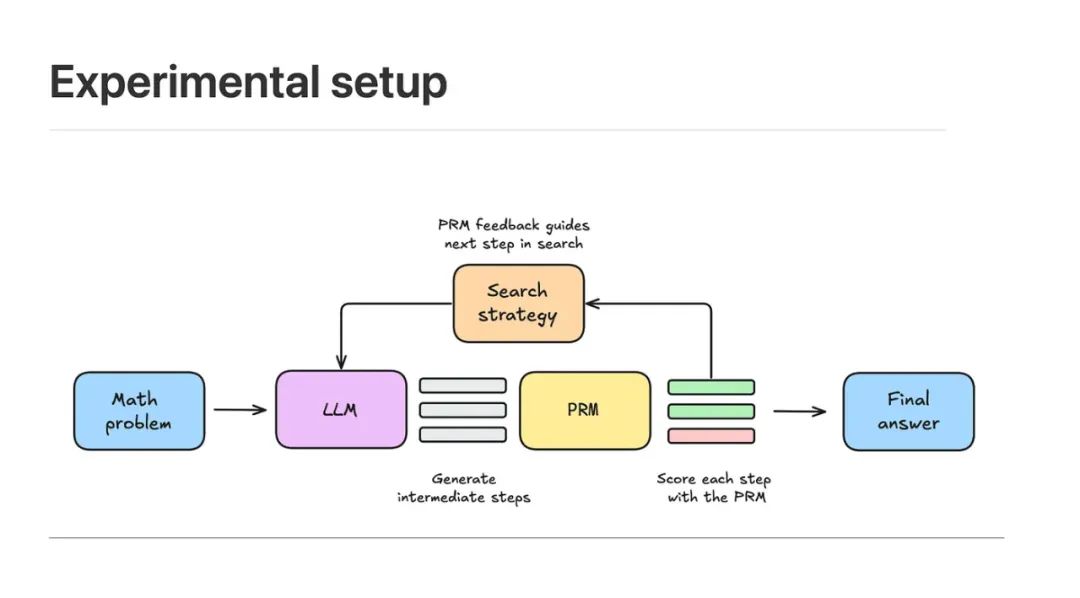
大白话的解释就是将一个数学问题输入大型语言模型（LLM），由模型生成 N 个中间解，即推导过程中的若干步骤或候选解法。这些中间解代表了模型在问题求解过程中可能采取的不同路径。

随后，利用过程奖励模型（Process Reward Model, PRM）对每个中间步骤进行打分，预测该步骤在未来推导中成功到达正确答案的可能性。根据这些得分结果，结合预设的搜索策略，筛选出值得进一步探索的部分解，并基于这些部分解生成下一轮中间步骤。

通过这种方式，逐步扩展解空间，同时在每个阶段利用PRM评估当前步骤的潜力，动态调整搜索方向。

当搜索过程达到终止条件（如达到计算预算或找到足够候选解）后，汇总所有最终候选答案，再次通过PRM对它们进行排序，最终选取得分最高的解作为模型的输出答案。

上图展示了几种外挂的TTS模式，

Best-of-N:

对每个问题生成 N 个候选答案，利用奖励模型（Reward Model）对每个答案打分，选取得分最高的作为最终输出。重点在于答案质量，而非生成概率。

Beam Search：

一种系统化的解空间搜索方法，结合过程奖励模型（PRM），在推理过程中为每个中间步骤打分，逐步筛选得分最高候选路径，提升整体推理质量。

Diverse verifier tree search (DVTS):

Beam Search 的改进版，将初始候选拆分为多个子树，分别在 PRM 指导下独立扩展，提升解的多样性和在高计算预算下的性能表现。

新的问题

最近有研究人员针对两个核心的问题进行深入分析：

(1) 在不同的策略模型、PRMs 和问题难度下，扩展推理计算的最优方式是什么？

(2) 延长推理计算时间能在多大程度上提升LLM在复杂任务上的表现？小模型是否可以通过这种方式超越大模型？

研究的结论表明在MATH-500和具有挑战性的AIME24数据集上

(1) 计算最优的TTS策略高度依赖于策略模型、PRM以及问题的难度；

(2) 利用合理的最优TTS策略，极小的策略模型可以超越大模型。

同时得到：

一个拥有1B参数的LLM在MATH-500任务上超越了405B参数的LLM
一个0.5B参数的模型超过了GPT-4o
一个3B参数的模型超过了405B参数的模型
一个7B参数的模型击败了o1和DeepSeek-R1，同时具有更高的推理效率

这些发现表明，针对具体任务和模型特征调整TTS策略至关重要，TTS方法在提升LLM推理能力方面具有广阔前景。

实验过程

数据集：

研究人员在竞赛级别的数学数据集上进行实验，包括MATH-500和AIME24。MATH-500和AIME24MATH-500包含来自MATH测试集的500个代表性问题，由于最近的大型语言模型在数学推理方面取得了显著进展还包括了更具挑战性AIME24进行实验。

策略模型：

对于TTS，使用来自Llama 3和Qwen2.5系列的不同大小的策略模型。我们为所有策略模型使用Instruct版本。

过程奖励模型：

基本上采用开源PRM进行评估：

• Math-Shepherd：Math-Shepherd-PRM-7B在Mistral-7B上进行训练，使用的是从Mistral-7B在MetaMath上微调生成的PRM数据。

• RLHFlow系列：RLHFlow包括RLHFlow-PRM-Mistral-8B和RLHFlow-PRM-Deepseek-8B，分别在Mistral-7B在MetaMath上微调的数据和deepseek-math-7b-instruct上进行训练。这两个PRM的基础模型都是Llama-3.1-8B-Instruct。

• Skywork系列：Skywork系列包括Skywork-PRM-1.5B和Skywork-PRM-7B，分别在Qwen2.5-Math-1.5B-Instruct和Qwen2.5-Math-7B-Instruct上进行训练。训练数据是从Llama-2在数学数据集上微调和Qwen2-Math系列模型生成的。

• Qwen2.5-Math系列：我们评估Qwen2.5-Math-PRM-7B和Qwen2.5-Math-PRM-72B，分别在Qwen2.5-Math-7B-Instruct和Qwen2.5-Math-72B-Instruct上进行训练。训练数据是使用Qwen2-Math和Qwen2.5-Math系列模型生成的。

在所有列出的PRM中，Qwen2.5-Math-PRM-72B是最强的开源数学任务PRM，而Qwen2.5-Math-PRM-7B是7B/8B参数中最有能力的PRM

评分和投票方法

三种评分方法：PRM-Min、PRM-Last和PRM-Avg，以及三种投票方法：Majority Vote、PRM-Max和PRM-Vote。、

下图为不同TTS和PRM组合在MATH-500和AIME24两个任务上的多次实验结果：

注意x轴代表实验次数，2的几次方！看来还是pass@k最高效，但是开销也是巨大的。

如上图所示，对于Llama-3.1-8B-Instruct，使用Skywork和Qwen2.5-Math PRMs的搜索方法在更大的计算预算下性能显著提升，而使用Math-Shepherd和RLHFlow PRMs的搜索结果相对较差，甚至比多数投票还差。

对于Qwen2.5-7B-Instruct，使用Skywork-PRM-7B和Qwen2.5-Math PRMs的搜索性能随着预算的增加而提升，而其他PRMs的性能仍然较差。

最佳的TTS方法取决于所使用的PRM。当使用Math-Shepherd和RLHFlow PRMs时，BoN大多数时候优于其他策略，而搜索方法在使用Skywork和Qwen2.5-Math PRMs时表现更好。这种差异是因为使用PRM处理OOD策略响应会导致次优答案，因为PRMs在策略模型之间的泛化能力有限。此外，如果我们使用OOD PRMs选择每一步，可能会陷入局部最优解并降低性能。