【CV知识点汇总与解析】|损失函数篇

【CV知识点汇总与解析】|损失函数篇

【写在前面】

本系列文章适合Python已经入门、有一定的编程基础的学生或人士，以及人工智能、算法、机器学习求职的学生或人士。系列文章包含了深度学习、机器学习、计算机视觉、特征工程等。相信能够帮助初学者快速入门深度学习，帮助求职者全面了解算法知识点。

1、 机器学习中常见的损失函数及其应用场景？

用于分类问题：

0-1损失函数：

$$L_{0-1}(f,y)=1_{fy\le 0}$$

0-1损失函数可以直观的刻画分类的错误率，但是因为其非凸，非光滑的特点，使得算法很难对其进行直接优化

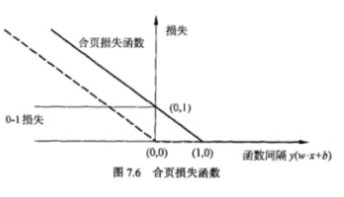
Hinge损失函数(SVM)

L hinge  ( f , y ) = max ⁡ { 0 , 1 − f y } L_{\text {hinge }}(f, y)=\max \{0,1-f y\} Lhinge ​(f,y)=max{0,1−fy}

Hinge损失函数是0-1损失函数的一个代理损失函数，也是其紧上界，当$fy\ge 0$ 时，不对模型做惩罚。可以看到，hinge损失函数在$fy=1$处不可导，因此不能用梯度下降法对其优化，只能用次梯度下降法。

Logistic损失函数

$$L_{\text{logistic }}(f,y)={\log }_2(1+\exp (-fy))$$

Logistic损失函数是0-1损失函数的另一个代理损失函数，它也是0-1损失函数的凸上界，且该函数处处光滑。但是该损失函数对所有样本点都惩罚，因此对异常值更加敏感。当预测值$ f ∈ [ − 1 , 1 ] $时，另一个常用的代理损失函数是交叉熵损失函数

Cross-Entropy损失函数

$$L_{\text{cross entropy }}(f,y)=-{\log }_2\left(\frac{1+fy}{2}\right)$$

交叉熵损失函数也是0-1损失函数的光滑凸上界

Exponential损失函数(AdaBoost)

$$L_{\text{exponential }}(f,y)=e^{-fy}$$

指数损失函数是AdaBoost里使用的损失函数，同样地，它对异常点较为敏感，鲁棒性不够

Logistic损失函数(LR)

$$L_{\text{logloss }}(y,p(y\mid x))=-\log (p(y\mid x))$$

逻辑回归$ p ( y ∣ x ) $的表达式如下：

$$P\left(Y=y^{(i)}\mid x^{(i)},\theta \right)=\{\begin{array}{l}{h}_{\theta }\left(x^{(i)}\right)=\frac{1}{1+e^{{\theta }_x}},y^{(i)}=1\\ 1-h_{\theta }\left(x^{(i)}\right)=\frac{e^{{\theta }^{T_x}}}{1+e^{{\theta }_x}},y^{(i)}=0,\end{array}$$

将上面两个式子合并，可得第 i 个样本被正确预测的概率：

$$P\left(Y=y^{(i)}\mid x^{(i)},\theta \right)={\left(h_{\theta }\left(x^{(i)}\right)\right)}^{y^{(i)}}{\left(1-h_{\theta }\left(x^{(i)}\right)\right)}^{1-y^{(i)}}$$

对于所有的样本，由于生成过程是独立的，因此

$$P(Y\mid X,\theta )={\Pi }_{i=1}^N{\left(h_{\theta }\left(x^{(i)}\right)\right)}^{y^{(i)}}{\left(1-h_{\theta }\left(x^{(i)}\right)\right)}^{1-y^{(i)}}$$

最终的损失函数如下：

$$\mathcal{J}(\theta )=-\sum _{i=1}^N\left[y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)\right]$$

用于回归问题：

对于回归问题，$Y=\mathbb{R}$，我们希望$f\left(x^{(i)},\theta \right)=y^{(i)}$

平方损失函数(最小二乘法)

$$L_{\text{square }}(f,y)=(f-y{)}^2$$

平方损失函数是光滑的，可以用梯度下降法求解，但是，当预测值和真实值差异较大时，它的惩罚力度较大，因此对异常点较为敏感。

绝对损失函数

$$L_{\text{absolute }}(f,y)=|f-y|$$

绝对损失函数对异常点不那么敏感，其鲁棒性比平方损失更强一些，但是它在$f=y$处不可导

Huber损失函数

$$L_{Huber}(f,y)=\{\begin{array}{l}\frac{1}{2}(f-y{)}^2,|f-y|\le \delta \\ \delta |f-y|-\frac{1}{2}{\delta }^2,|f-y|>\delta ,\end{array}$$

Huber损失函数在 ∣ f − y ∣较小时为平方损失，在 ∣ f − y ∣ 较大时为线性损失，且处处可导，对异常点鲁棒性较好。

Log-cosh损失函数

$$L_{\log -\cosh }(f,y)=\log (\cosh (f-y))$$

其中 $\cosh (x)=\left(e^x+e^{-x}\right)/2$，log-cosh损失函数比均方损失函数更加光滑，具有huber损失函数的所有优点，且二阶可导。因此可以使用牛顿法来优化计算，但是在误差很大情况下，一阶梯度和Hessian会变成定值，导致牛顿法失效。

分位数损失函数

$$L_{\gamma }(f,y)=\sum _{i:y_i<f_i}(1-\gamma )\left|y_i-f_i\right|+\sum _{i:y_i\ge f_i}\gamma \left|y_i-f_i\right|$$

预测的是目标的取值范围而不是值。γ 是所需的分位数，其值介于0和1之间，γ 等于0.5时，相当于MAE。设置多个 γ 值，得到多个预测模型，然后绘制成图表，即可知道预测范围及对应概率(两个 γ值相减)

用于检索问题

Triplet loss

$$\sum _i^N{\left[{\Vert f\left(x_i^a\right)-f\left(x_i^p\right)\Vert }_2^2-{\Vert f\left(x_i^a\right)-f\left(x_i^n\right)\Vert }_2^2+\alpha \right]}_{+}$$

[]_+相当于一个ReLU函数。三元组的构成：从训练数据集中随机选一个样本，该样本称为Anchor，然后再随机选取一个和Anchor属于同一类的样本和不同类的样本,这两个样本对应的称为Positive 和Negative，由此构成一个三元组。

通过学习，让正样本特征表达之间的距离尽可能小，而负样本的特征表达之间的距离尽可能大，并且要让正样本之间的距离和负样本之间的距离之间有一个最小的间隔（margin）。 损失函数如下所示：

Sum Hinge Loss & Max Hinge Loss

Triplet loss 的输入是 (a, p, n)，一般的做法是 b 个$\left(a_i,p_i\right)i\in [0,b]$pair 对，我们对 pi 旋转一下得到$\left(p_1,p_2,\dots ,p_b,p_0\right)$作为负样本列表。最后得到一个一维的 loss 向量$\left(l_1,l_2\dots ,l_b\right)$。

Triplet loss 实际上只考虑了由 a 和 p 组成矩阵的部分情况产生的loss，我们实际上可以对 a、p 产生的相似度矩阵中所有非对角线的负样本进行计算损失，从而充分利用 batch 内的信息，通过这个思路我们可以得到 Sum Hinge Loss 如下，Triplet loss 的计算中是用的 L2 距离，这里改为了余弦相似度，所以之前的 ap - an + margin，改为了 an - ap + margin 了，目标是让 an 的相似度更小，ap 的相似度更大

Sum Hinge Loss：

$${\ell }_{SH}(i,c)=\sum _{\hat{c}}[\alpha -s(i,c)+s(i,\hat{c})]++\sum \hat{i}[\alpha -s(i,c)+s(\hat{i},c){]}_{+}$$

Max Hinge Loss：

VSE++ 提出了一个新的损失函数max hinge loss，它主张在排序过程中应该更多地关注困难负样例，困难负样本是指与anchor靠得近的负样本，实验结果也显示max hinge loss性能比之前常用的排序损失sum hinge loss好很多：

$${\ell }_{MH}(i,c)=\max c^{\prime }\left[\alpha +s\left(i,c^{\prime }\right)-s(i,c)\right]++\max i^{\prime }\left[\alpha +s\left(i^{\prime },c\right)-s(i,c)\right]+$$

Max Hinge Loss pytorch 代码如下：

def cosine_sim(im, s):
    """Cosine similarity between all the image and sentence pairs
    """
    return im.mm(s.t())

class MaxHingLoss(nn.Module):

    def __init__(self, margin=0.2, measure=False, max_violation=True):
        super(MaxHingLoss, self).__init__()
        self.margin = margin
        self.sim = cosine_sim
        self.max_violation = max_violation

    def forward(self, im, s):
        an = self.sim(im, s) # an
        diagonal = scores.diag().view(im.size(0), 1)
        ap1 = diagonal.expand_as(scores)
        ap2 = diagonal.t().expand_as(scores)

        # query2doc retrieval
        cost_s = (self.margin + an - ap1).clamp(min=0)
        # doc2query retrieval
        cost_im = (self.margin + an - ap2).clamp(min=0)

        # clear diagonals
        mask = torch.eye(scores.size(0)) > .5
        I = Variable(mask)
        if torch.cuda.is_available():
            I = I.cuda()
        cost_s = cost_s.masked_fill_(I, 0)
        cost_im = cost_im.masked_fill_(I, 0)
        # keep the maximum violating negative for each query
        if self.max_violation:
            cost_s = cost_s.max(1)[0][:1]
            cost_im = cost_im.max(0)[0][:1]
        return cost_s.mean() + cost_im.mean()
        # or # return cost_s.sum() + cost_im.sum()

Info NCE

Info NCE loss是NCE的一个简单变体，它认为如果你只把问题看作是一个二分类，只有数据样本和噪声样本的话，可能对模型学习不友好，因为很多噪声样本可能本就不是一个类，因此还是把它看成一个多分类问题比较合理（但这里的多分类 k 指代的是负采样之后负样本的数量），于是就有了InfoNCE loss 函数如下：

$$L_q=-\log \frac{\exp \left(q\cdot k_{+}/\tau \right)}{{\sum }_{i=0}^k\exp \left(q\cdot k_i/\tau \right))}$$

其中$q\cdot k$相当于是 logits， $\tau$是温度系数，整体和 cross entropy 是非常相近的。

用于检测问题：

类别损失

Softmax+交叉熵

对于二分类而言，交叉熵损失函数形式如下：

$$\mathrm{L}=-\mathrm{ylog}{y}^{\prime }-(1-y)\log \left(1-y^{\prime }\right)=\{\begin{array}{ll}-\log y^{\prime },& y=1\\ -\log \left(1-y^{\prime }\right),& y=0\end{array}$$

交叉熵损失函数通过不断缩小两个分布的差异，使预测结果更可靠。

Focal Loss

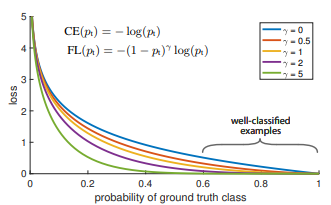
focal loss出于论文Focal Loss for Dense Object Detection，主要是为了解决one-stage目标检测算法中正负样本比例严重失衡的问题，降低了大量简单负样本在训练中所占的比重，可理解为是一种困难样本挖掘。focal loss是在交叉熵损失函数上修改的。具体改进：

$${\mathrm{L}}_{fl}=\{\begin{array}{cc}-\alpha {\left(1-y^{\prime }\right)}^{\gamma }\log y^{\prime },& y=1\\ -(1-\alpha )y^{\prime \gamma }\log \left(1-y^{\prime }\right),& y=0\end{array}$$

其中γ>0(文章中取2）使得减少易分类样本的损失，更关注困难的、错分的样本。例如γ为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的γ次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。
此外加入平衡因子α，用来平衡正负样本本身的比例不均，文中取值为0.25，即正样本比负样本占比小，这是因为负例易分

位置损失

L1（MAE），L2（MSE），smooth L1损失函数

利用L1，L2或者smooth L1损失函数，来对4个坐标值进行回归。smooth L1损失函数是在Fast R-CNN中提出的。三个损失函数，如下所示：

$$\begin{gathered} L1=|x| \\ L2=x^2 \\ smoothL1=\{\begin{array}{cc}0.5x^2& \text{ if }|x|<1\\ |x|-0.5& \text{ otherwise }\end{array} \end{gathered}$$

从损失函数对x的导数可知：L1损失函数对x的导数为常数，不会有梯度爆炸的问题，但其在0处不可导，在较小损失值时，得到的梯度也相对较大，可能造成模型震荡不利于收敛。L2损失函数处处可导，但由于采用平方运算，当预测值和真实值的差值大于1时，会放大误差。尤其当函数的输入值距离中心值较远的时候，使用梯度下降法求解的时候梯度很大，可能造成梯度爆炸。同时当有多个离群点时，这些点可能占据Loss的主要部分，需要牺牲很多有效的样本去补偿它，所以L2 loss受离群点的影响较大。smooth L1完美的避开了L1和L2损失的缺点：

• 在[-1,1]之间就是L2损失，解决L1在0处有折点

• 在[-1，1]区间以外就是L1损失，解决离群点梯度爆炸问题

• 当预测值与真实值误差过大时，梯度值不至于过大

• 当预测值与真实值误差很小时，梯度值足够小

上述3个损失函数存在以下不足：

• 上述三个损失函数在计算bounding box regression loss时，是独立的求4个点的loss，然后相加得到最终的损失值，这种做法的前提是四个点是相互独立的，而实际上是有一定相关性的

• 实际评价检测结果好坏的指标是IoU，这两者是不等价的，多个检测框可能有相同的loss，但IoU差异很大

IoU Loss

IoU loss的定义如下：

$$L_I=1-\frac{P\cap G}{P\cup G}$$

其中P代表预测框，G代表真实框。

GIoU loss

IoU反映了两个框的重叠程度，在两个框不重叠时，IoU衡等于0，此时IoU loss恒等于1。而在目标检测的边界框回归中，这显然是不合适的。因此，GIoU loss在IoU loss的基础上考虑了两个框没有重叠区域时产生的损失。具体定义如下：

$$L_G=1-IoU+R(P,G)=1-IoU+\frac{|C-P\cup G|}{|C|}$$

其中，C表示两个框的最小包围矩形框，R(P,G)是惩罚项。从公式可以看出，当两个框没有重叠区域时，IoU为0，但R依然会产生损失。极限情况下，当两个框距离无穷远时，R→1

DIoU Loss

IoU loss和GIoU loss都只考虑了两个框的重叠程度，但在重叠程度相同的情况下，我们其实更希望两个框能挨得足够近，即框的中心要尽量靠近。因此，DIoU在IoU loss的基础上考虑了两个框的中心点距离，具体定义如下：

$$L_G=1-IoU+R(P,G)=1-IoU+\frac{{\rho }^2(p,g)}{c^2}$$

其中，ρ表示预测框和标注框中心端的距离，p和g是两个框的中心点。c表示两个框的最小包围矩形框的对角线长度。当两个框距离无限远时，中心点距离和外接矩形框对角线长度无限逼近，R→1。

CIoU Loss

DIoU loss考虑了两个框中心点的距离，而CIoU loss在DIoU loss的基础上做了更详细的度量，具体包括：

• 重叠面积

• 中心点距离

• 长宽比

具体定义如下：

$$L_G=1-IoU+R(P,G)=1-IoU+\frac{{\rho }^2(p,g)}{c^2}+\alpha v$$

$$\begin{gathered} v=\frac{4}{{\pi }^2}{\left(\arctan \frac{w^g}{h^g}-\arctan \frac{w^p}{h^p}\right)}^2 \\ \alpha =\frac{v}{(1-IoU)+v} \end{gathered}$$

用于分割问题

dice Loss

dice loss 源于dice系数，是用于度量集合相似度的度量函数，通常用于计算两个样本之间的相似度，公式如下：

$$Dice=\frac{2|\mathrm{X}\cap Y|}{|X|+|Y|}$$

那么对应的dice loss的公式如下：

$$Diceloss=1-\frac{2|\mathrm{X}\cap Y|}{|X|+|Y|}$$

根据dice loss的定义可以看出，dice loss是一种区域相关的loss，也即意味着某像素点的loss以及梯度值不仅和该点的label和预测值相关，也与其他点的label及预测值相关。dice loss可用于样本极度不均衡的情况，而在一般情况下使用dice loss会对反向传播有不利的影响，使得训练不稳定。

交叉熵

语义分割任务中最常用的损失函数是交叉熵，通过逐个对比每个像素得到损失值。

每个像素对应的损失函数为：

$$pixel-loss=-\sum _{\text{classes }}\left(y_c\log \left(p_c\right)\right)$$

$y_c$为一个one-hot向量，取值只有[0, 1]，$p_c$为网络预测值经过softmax或sigmoid函数之后的概率值。

整个图像的损失就是每个像素的损失求平均。交叉熵损失函数适用于大多数语义分割场景中，但是当前景像素的数量远小于背景像素的数量时，此时背景的损失占主导地位，导致网络性能不佳。

带权值的交叉熵

针对类别不平衡的问题，通过给每个类别添加一个权重系数来缓解。加上权重之后的公式如下：

$$pixel-loss=-\sum _c^{\text{classes }}\left(w_c{y}_c\log \left(p_c\right)\right)$$

其中$w_c=\frac{N-N_c}{N}$，$N$表示总的像素个数，而$N_c$表示GT类别为c的像素个数。

2、为什么不能将识别精度作为指标？

以数字识别任务为例，我们想获得的是能提高识别精度的参数，特意再导入一个损失函数不是有些重复劳动吗？也就是说，既然我们的目标是获得使识别精度尽可能高的神经网络，那不是应该把识别精度作为指标吗？

在进行神经网络的学习时，不能将识别精度作为指标，因为如果以识别精度为指标，导数大多数情况下都为0。导数为0会导致权重参数的更新会停下来。

3、 为什么LogSoftmax比Softmax更好？

log_softmax能够解决函数overflow和underflow，加快运算速度，提高数据稳定性。

因为softmax会进行指数操作，当上一层的输出，也就是softmax的输入比较大的时候，可能就会产生overflow。同理当输入为负数且绝对值也很大的时候，会分子、分母会变得极小，有可能四舍五入为0，导致下溢出。

尽管在数学表示式上是对softmax在取对数的情况。但是在实操中是通过：

$$\begin{gathered} \log \left[f\left(x_i\right)\right]=\log \left(\frac{e^{x_i}}{e^{x_1}+e^{x_2}+\dots +e^{x_n}}\right) \\ =\log \left(\frac{\frac{e^{x_i}}{e^M}}{\frac{e^{x_1}}{e^M}+\frac{e^2}{e^M}+\dots +\frac{e^{x_n}}{e^M}}\right)=\log \left(\frac{e^{\left(x_i-M\right)}}{{\sum }_j^n{e}^{\left(x_j-M\right)}}\right) \\ =\log \left(e^{\left(x_i-M\right)}\right)-\log \left(\sum _j^n{e}^{\left(x_j-M\right)}\right)=\left(x_i-M\right)-\log \left(\sum _j^n{e}^{\left(x_j-M\right)}\right) \end{gathered}$$

来实现，其中 $M=\max \left(x_i\right),i=1,2,\cdots ,n$，即 M为所有$x_i$中最大的值。可以解决这个问题，在加快运算速度的同时，可以保持数值的稳定性。

4、 什么是label smoothing？为什么要用label smoothing？

label smoothing是一种正则化的方式，全称为Label Smoothing Regularization(LSR)，即标签平滑正则化。

在传统的分类任务计算损失的过程中，是将真实的标签做成one-hot的形式，然后使用交叉熵来计算损失。而label smoothing是将真实的one hot标签做一个标签平滑处理，使得标签变成又概率值的soft label.其中，在真实label处的概率值最大，其他位置的概率值是个非常小的数。

在label smoothing中有个参数epsilon，描述了将标签软化的程度，该值越大，经过label smoothing后的标签向量的标签概率值越小，标签越平滑，反之，标签越趋向于hard label，在训练ImageNet-1k的实验里通常将该值设置为0.1。

5、在用sigmoid或softmax作为激活函数的时候，为什么要用交叉熵损失函数，而不用均方误差损失函数？

1. 因为交叉熵损失函数可以完美解决平方损失函数权重更新过慢的问题，具有“误差大的时候，权重更新快；误差小的时候，权重更新慢”的良好性质。
2. sigmoid作为激活函数的时候，如果采用均方误差损失函数，那么这是一个非凸优化问题，不宜求解。而采用交叉熵损失函数依然是一个凸优化问题，更容易优化求解。

公式推导详解见：https://blog.csdn.net/weixin_41888257/article/details/104894141

6、 关于交叉熵损失函数（Cross-entropy）和 平方损失（MSE）的区别？

1. 概念区别

**均方差损失函数（MSE）：**简单来说，均方误差（MSE）的含义是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值。

Cross-entropy（交叉熵损失函数)：交叉熵是用来评估当前训练得到的概率分布与真实分布的差异情况。它刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。

2. 应用场景

MSE更适合回归问题，交叉熵损失函数更适合分类问题。

7、什么是KL散度？

KL散度定义

KL(Kullback-Leibler divergence)散度多应用于概率论或信息论中，又可称相对熵(relative entropy)。它是用来描述两个概率分布P和Q的差异的一种方法。

KL具有非对称性，即D(P||Q) ≠ D(Q||P)。
在信息论中，D(P||Q) 表示用概率分布Q来拟合真实分布P时，产生的信息损耗，其中P表示真实分布，Q表示P的拟合分布

KL散度公式定义

对于离散型随机变量有：

$$\mathrm{D}(\mathrm{P}\Vert \mathrm{Q})=\sum _{i\in X}P(i)\ast \left[\log \left(\frac{P(i)}{Q(i)}\right)\right]$$

对于连续型随机变量有：

$$\mathrm{D}(\mathrm{P}\Vert \mathrm{Q})={\int }_{x}P(x)\ast \left[\log \left(\frac{P(i)}{Q(i)}\right)\right]dx$$

KL散度的物理定义

在信息论中，它是用来度量使用基于Q分布的编码来编码来自P分布的样本平均所需的额外的比特(bit)个数。
在机器学习领域，是用来度量两个函数的相似程度或者相近程度。

8、手写IOU、GIOU、DIOU、CIOU的代码

IOU代码及结果展示如下

import cv2
import numpy as np
def IOU_score(box1,box2):
        """
        计算两个区域的iou的值

        para: box1 区域1的两个角的坐标值  x1,y1,x2,y2
        para: box2 区域2的两个角的坐标值  x1,y1,x2,y2
        """
        # 两个框的交
        iou_x1 = max(box1[0], box2[0])
        iou_y1 = max(box1[1], box2[1])
        iou_x2 = min(box1[2], box2[2]) 
        iou_y2 = min(box1[3], box2[3])

        # 上面求出来的为交集的两个角的坐标
        area_inter = max(0,(iou_x2 - iou_x1)) * max(0 , (iou_y2 - iou_y1))

        # 计算两个区域的并集
        area_all = ((box1[2] - box1[0]) * (box1[3] - box1[1])) + ((box2[2] - box2[0]) * (box2[3] - box2[1])) - area_inter
        
        center_x = int((iou_x1 + iou_x2) / 2)
        center_y = int((iou_y2 + iou_y1) / 2)
        return float(area_inter / area_all) , (center_x,center_y)

def main():

    img = np.zeros((512,512,3), np.uint8)   
    img.fill(255)

    box1 = [50,50,300,300]
    box2 = [51,51,301,301]

    cv2.rectangle(img, (box1[0],box1[1]), (box1[2],box1[3]), (0, 0, 255), 2)
    cv2.rectangle(img, (box2[0],box2[1]), (box2[2],box2[3]), (255, 0, 0), 2)

    IOU , center = IOU_score(box1,box2)
    font = cv2.FONT_HERSHEY_SIMPLEX
    cv2.putText(img,"IOU = %.2f"%IOU,center,font,0.8,(0,0,0),2)

    cv2.imshow("image",img)
    cv2.waitKey()
    cv2.destroyAllWindows()

if __name__ == "__main__":
    main()

GIOU代码及结果展示如下

import cv2
import numpy as np
def GIOU_score(box1,box2):
        """
        计算两个区域的iou的值

        para: box1 区域1的两个角的坐标值  x1,y1,x2,y2
        para: box2 区域2的两个角的坐标值  x1,y1,x2,y2
        """
        # 两个框的交
        iou_x1 = max(box1[0], box2[0])
        iou_y1 = max(box1[1], box2[1])
        iou_x2 = min(box1[2], box2[2]) 
        iou_y2 = min(box1[3], box2[3])

        g_iou_x1 = min(box1[0], box2[0]) 
        g_iou_y1 = min(box1[1], box2[1])
        g_iou_x2 = max(box1[2], box2[2]) 
        g_iou_y2 = max(box1[3], box2[3])

        # 上面求出来的为交集的两个角的坐标
        area_inter = max(0,(iou_x2 - iou_x1)) * max(0 , (iou_y2 - iou_y1))

        # 计算两个区域的并集
        area_union = max(0,((box1[2] - box1[0]) * (box1[3] - box1[1])) + ((box2[2] - box2[0]) * (box2[3] - box2[1])) - area_inter)

        # 计算最小外接矩形
        area_all = max(0,(g_iou_x2 - g_iou_x1) * (g_iou_y2 - g_iou_y1))

        g_iou = max(0,area_inter/area_union) - max(0,area_all - area_union) / area_all 

        return float(g_iou) , (iou_x1,iou_y1,iou_x2,iou_y2) , (g_iou_x1,g_iou_y1,g_iou_x2,g_iou_y2)

def main():

    img = np.zeros((512,512,3), np.uint8)   
    img.fill(255)

    box1 = [50,50,300,300]
    box2 = [100,100,400,400]

    IOU , area_inter , area_all = GIOU_score(box1,box2)

    font = cv2.FONT_HERSHEY_SIMPLEX
    cv2.putText(img,"GIOU = %.2f"%IOU,(area_inter[0]+30,area_inter[1]+30),font,0.8,(0,0,0),2)

    cv2.rectangle(img, (box1[0],box1[1]), (box1[2],box1[3]), (255, 0, 0),  thickness = 3)
    cv2.rectangle(img, (box2[0],box2[1]), (box2[2],box2[3]), (0, 255, 0), thickness = 3)
    cv2.rectangle(img, (area_all[0],area_all[1]), (area_all[2],area_all[3]), (0, 0, 255), thickness = 3)
    
    cv2.imshow("image",img)
    cv2.waitKey()
    cv2.destroyAllWindows()


if __name__ == "__main__":
    main()

DIOU代码及结果展示如下

import cv2
import numpy as np
def DIOU_score(box1,box2):
        """
        计算两个区域的iou的值

        para: box1 区域1的两个角的坐标值  x1,y1,x2,y2
        para: box2 区域2的两个角的坐标值  x1,y1,x2,y2
        """
        # 两个框的交
        iou_x1 = max(box1[0], box2[0])
        iou_y1 = max(box1[1], box2[1])
        iou_x2 = min(box1[2], box2[2]) 
        iou_y2 = min(box1[3], box2[3])

        d_x1 = max(0, (box1[2] + box1[0])/2)
        d_y1 = max(0, (box1[3] + box1[1])/2)
        d_x2 = max(0, (box2[2] + box2[0])/2)
        d_y2 = max(0, (box2[3] + box2[1])/2)

        c_x1 = min(box1[0], box2[0]) 
        c_y1 = min(box1[1], box2[1])
        c_x2 = max(box1[2], box2[2]) 
        c_y2 = max(box1[3], box2[3])

        # 上面求出来的为交集的两个角的坐标
        area_inter = max(0,(iou_x2 - iou_x1)) * max(0 , (iou_y2 - iou_y1))

        # 计算两个区域的并集
        area_union = max(0,((box1[2] - box1[0]) * (box1[3] - box1[1])) + ((box2[2] - box2[0]) * (box2[3] - box2[1])) - area_inter)

        # 计算最小外接矩形
        c_2 = max(0,(c_x2 - c_x1))**2 + max(0,(c_y2 - c_y1))**2
        d_2 =  max(0,(d_x2 - d_x1))**2 + max(0,(d_y2 - d_y1))**2

        g_iou = max(0,area_inter/area_union) - d_2/c_2

        return float(g_iou) , (iou_x1,iou_y1,iou_x2,iou_y2) , (c_x1,c_y1,c_x2,c_y2), (int(d_x1),int(d_y1),int(d_x2),int(d_y2))

def main():
    img = np.zeros((512,512,3), np.uint8)   
    img.fill(255)

    box1 = [50,50,300,300]
    box2 = [250,80,400,350]

    IOU , area_inter , area_all , short_line = DIOU_score(box1,box2)

    font = cv2.FONT_HERSHEY_SIMPLEX
    cv2.putText(img,"GIOU = %.2f"%IOU,(area_inter[0]+30,area_inter[1]+30),font,0.8,(0,0,0),2)

    cv2.rectangle(img, (box1[0],box1[1]), (box1[2],box1[3]), (255, 0, 0),  thickness = 3)
    cv2.rectangle(img, (box2[0],box2[1]), (box2[2],box2[3]), (0, 255, 0), thickness = 3)
    cv2.rectangle(img, (area_all[0],area_all[1]), (area_all[2],area_all[3]), (0, 0, 255), thickness = 3)
    cv2.line(img, (short_line[0],short_line[1]), (short_line[2],short_line[3]), (200,45,45),5)
    cv2.line(img, (area_all[0],area_all[1]), (area_all[2],area_all[3]), (64,78,0),5)
    
    cv2.imshow("image",img)
    cv2.waitKey()
    cv2.destroyAllWindows()


if __name__ == "__main__":
    main()

CIOU代码及结果展示如下

import cv2
import numpy as np
from math import pi,atan
def CIOU_score(box1,box2):
        """
        计算两个区域的iou的值

        para: box1 区域1的两个角的坐标值  x1,y1,x2,y2
        para: box2 区域2的两个角的坐标值  x1,y1,x2,y2
        """
        # 两个框的交
        iou_x1 = max(box1[0], box2[0])
        iou_y1 = max(box1[1], box2[1])
        iou_x2 = min(box1[2], box2[2]) 
        iou_y2 = min(box1[3], box2[3])

        d_x1 = max(0, (box1[2] + box1[0])/2)
        d_y1 = max(0, (box1[3] + box1[1])/2)
        d_x2 = max(0, (box2[2] + box2[0])/2)
        d_y2 = max(0, (box2[3] + box2[1])/2)

        c_x1 = min(box1[0], box2[0]) 
        c_y1 = min(box1[1], box2[1])
        c_x2 = max(box1[2], box2[2]) 
        c_y2 = max(box1[3], box2[3])

        w_gt = max(0,box2[2] - box2[0])
        h_gt = max(0,box2[3] - box2[1])

        w    = max(0,box1[2] - box1[0])
        h    = max(0,box1[3] - box1[1])

        # 上面求出来的为交集的两个角的坐标
        area_inter = max(0,(iou_x2 - iou_x1)) * max(0 , (iou_y2 - iou_y1))

        # 计算两个区域的并集
        area_union = max(0,((box1[2] - box1[0]) * (box1[3] - box1[1])) + ((box2[2] - box2[0]) * (box2[3] - box2[1])) - area_inter)

        iou = max(0,area_inter/area_union)

        c_2 = max(0,(c_x2 - c_x1))**2 + max(0,(c_y2 - c_y1))**2
        d_2 =  max(0,(d_x2 - d_x1))**2 + max(0,(d_y2 - d_y1))**2

        v = 4/pi**2 * (atan(w_gt/h_gt) - atan(w/h))**2

        alpha = v / (1-iou + v)

        c_iou = iou - d_2/c_2 - alpha * v

        return float(c_iou) , (iou_x1,iou_y1,iou_x2,iou_y2) , (c_x1,c_y1,c_x2,c_y2), (int(d_x1),int(d_y1),int(d_x2),int(d_y2))

def main():
    img = np.zeros((512,512,3), np.uint8)   
    img.fill(255)

    box1 = [50,50,300,300]
    box2 = [100,80,200,260]

    IOU , area_inter , area_all , short_line = CIOU_score(box1,box2)

    font = cv2.FONT_HERSHEY_SIMPLEX
    cv2.putText(img,"GIOU = %.2f"%IOU,(area_inter[0]+30,area_inter[1]+30),font,0.8,(0,0,0),2)

    cv2.rectangle(img, (box1[0],box1[1]), (box1[2],box1[3]), (255, 0, 0),  thickness = 3)
    cv2.rectangle(img, (box2[0],box2[1]), (box2[2],box2[3]), (0, 255, 0), thickness = 3)
    cv2.rectangle(img, (area_all[0],area_all[1]), (area_all[2],area_all[3]), (0, 0, 255), thickness = 3)
    cv2.line(img, (short_line[0],short_line[1]), (short_line[2],short_line[3]), (200,45,45),5)
    cv2.line(img, (area_all[0],area_all[1]), (area_all[2],area_all[3]), (64,78,0),5)
    
    cv2.imshow("image",img)
    cv2.waitKey()
    cv2.destroyAllWindows()


if __name__ == "__main__":
    main()

9、代价函数，损失函数、目标函数、风险函数的区别？

• 损失函数（Loss Function ）是定义在单个样本上的，算的是一个样本的误差。

• 代价函数（Cost Function）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均。

• 目标函数（Object Function）定义为：最终需要优化的函数。等于经验风险+结构风险（也就是代价函数 + 正则化项）。代价函数最小化，降低经验风险，正则化项最小化降低。

• 风险函数(risk function)，风险函数是损失函数的期望，这是由于我们输入输出的(X,Y)遵循一个联合分布，但是这个联合分布是未知的，所以无法计算。但是我们是有历史数据的，就是我们的训练集，f(x) 关于训练集的平均损失称作经验风险(empirical risk)，即，所以我们的目标就是最小化 称为经验风险最小化。

10、噪声**、偏差和方差的区别是啥？**

• 噪声：描述了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。说人话，就是数据中的有些标签不是真的标签，也是有限噪声的标签。

• 偏差：是指预测结果与真实值之间的差异，排除噪声的影响，偏差更多的是针对某个模型输出的样本误差，偏差是模型无法准确表达数据关系导致，比如模型过于简单，非线性的数据关系采用线性模型建模，偏差较大的模型是错的模型。

• 方差：不是针对某一个模型输出样本进行判定，而是指多个(次)模型输出的结果之间的离散差异，注意这里写的是多个模型或者多次模型，即不同模型或同一模型不同时间的输出结果方差较大，方差是由训练集的数据不够导致，一方面量 (数据量) 不够，有限的数据集过度训练导致模型复杂，另一方面质(样本质量)不行，测试集中的数据分布未在训练集中，导致每次抽样训练模型时，每次模型参数不同，输出的结果都无法准确的预测出正确结果。

11、MSE对于异常样本的鲁棒性差的问题怎么解决？

1. 如果异常样本无意义，可以进行异常值的平滑或者直接删除。

2. 如果异常样本有意义，需要模型把这些有意义的异常考虑进来，则从模型侧考虑使用表达能力更强的模型或复合模型或分群建模等；

3. 在损失层面选择更鲁棒的损失函数。

12、熵的相关知识点？

• 信息量 度量一个事件的不确定性程度，不确定性越高则信息量越大，一般通过事件发生的概率来定义不确定性，信息量则是基于概率密度函数的log运算，用以下式子定义：

$$I(x)=-\log p(x)$$

• 信息熵 衡量的是一个事件集合的不确定性程度，就是事件集合中所有事件的不确定性的期望，公式定义如下：

$$H(X)=-\sum _{x\in X}[p(x)\log p(x)]$$

• 相对熵(KL散度) kl散度，从概统角度出发，表示用于两个概率分布的差异的非对称衡量，kl散度也可以从信息理论的角度出发，从这个角度出发的kl散度我们也可以称之为相对熵，实际上描述的是两个概率分布的信息熵的差值：

$$KL(P\Vert Q)=\sum P(x)\log \frac{P(x)}{Q(x)}$$

kl散度和余弦距离一样，不满足距离的严格定义；非负且不对称。

• js散度 公式如下：

$$JS(P\Vert Q)=\frac{1}{2}KL(P(x))\Vert \frac{P(x)+Q(x)}{2}+\frac{1}{2}KL(Q(x))\Vert \frac{P(x)+Q(x)}{2}$$

js散度的范围是[0,1],相同则是0，相反为1。相较于KL，对相似度的判别更准确;同时，js散度满足对称性 JS(P||Q)=JS(Q||P)

• 交叉熵 公式如下：

$$H(P,Q)=-\sum p\log q=H(P)+D_{kl}(P\Vert Q)$$

可见,交叉熵就是真值分布的信息熵与KL散度的和,而真值的熵是确定的,与模型的参数θ 无关,所以梯度下降求导时，优化交叉熵和优化kl散度（相对熵）是一样的；

• 联合熵 公式如下：

$$H(X,Y)=-\sum _{x,y}p(x,y)\log p(x,y)$$

联合熵实际上衡量的是两个事件集合，经过组合之后形成的新的大的事件集合的信息熵；

• 条件熵 公式如下：

$$H(Y\mid X)=H(X,Y)-H(X)$$

事件集合Y的条件熵=联合熵-事件集合X的信息熵，用来衡量在事件集合X已知的基础上，事件集合Y的不确定性的减少程度；

13、怎么衡量两个分布的差异？

使用KL散度或者JS散度

14、Huber Loss 有什么特点？

Huber Loss 结合了 MSE 和 MAE 损失，在误差接近 0 时使用 MSE，使损失函数可导并且梯度更加稳定；在误差较大时使用 MAE 可以降低 outlier 的影响，使训练对 outlier 更加健壮。缺点是需要额外地设置一个超参数。

15、如何理解Hinger Loss？

可以看到，当x大于某个值的时候，loss为0，当x小于某个值的时候，那就需要算loss了，说明模型对小于阈值的样本进行了惩罚，而且越大惩罚的越厉害，对于大于阈值的样本不进行惩罚，总的来说就是该损失函数寻找一个边界，对具有可信的样本不惩罚，对不可信的样本或者超出决策边界的样本进行惩罚。

【项目推荐】

面向小白的顶会论文核心代码库：https://github.com/xmu-xiaoma666/External-Attention-pytorch

面向小白的YOLO目标检测库：https://github.com/iscyy/yoloair

面向小白的顶刊顶会的论文解析：https://github.com/xmu-xiaoma666/FightingCV-Paper-Reading

参考：

https://blog.csdn.net/zuolixiangfisher/article/details/88649110

https://zhuanlan.zhihu.com/p/514859125

https://blog.csdn.net/weixin_43750248/article/details/116656242

https://blog.csdn.net/hello_dear_you/article/details/121078919

https://blog.csdn.net/weixin_41888257/article/details/104894141

https://blog.csdn.net/weixin_37763870/article/details/103026505

https://blog.csdn.net/to_be_little/article/details/124674924

https://zhuanlan.zhihu.com/p/548782472