Variant AutoEncoder(VAE)和 VQVAE 学习笔记和代码

参考：
[1] VAE1
[2] https://lilianweng.github.io/posts/2018-08-12-vae/
[3] VAE Code

1 VAE

1.1 VAE的直观理解

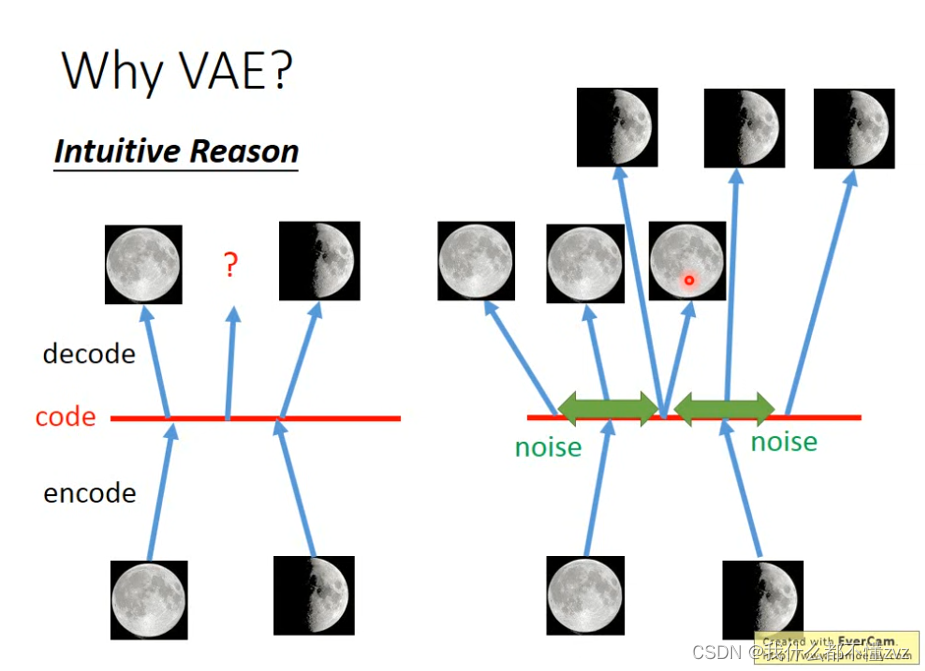
最直观的图莫过于[李宏毅ML18讲]以上这幅图。 对于AutoEncoder模型，模型其实是在拟合一个identity function，也就是对于每个输入$x$，在隐空间(latant space)都有唯一的隐变量$z$与之对应，那么生成的$x^{\prime }$同理可知也是和$x、z$唯一对应的。

那么问题来了，在采样过程中，由于隐变量$z$所在的分布是连续的，我们的数据集 { x } \{x\} {x}又是有限的，所以不可能将所有的$z$都和$x或x^{\prime }$对应上。而神经网络通常又是非线性的，对于一些从来没有见过的隐变量，也不可能通常线性关系去推导它对应的$x^{\prime }$是啥样的（比如上图中，满月和半月之间的$z$对应的月亮大概率不是一个$\frac{2}{3}$月亮，因为non-linear的原因）

而VAE机智的地方在于，它让每一个$x$都对应一个随机分布，而不再是对应一个隐变量，那么上面提到的$\frac{2}{3}$个月亮，可能就是两个分布的重叠部分，那么可以根据权值或者什么方式得到相应的月亮图。总之，观测数据$x$不再是对应于一个值，而是对应于一个分布，我们在这个分布里采样，就可以得到不同的图像，此时模型就变成了生成模型。

1.2 VAE数学推导

1.2.1 混合高斯模型角度理解VAE（李宏毅ML课的说法）

混合高斯模型（mixture-gaussian model）可以简单定义为： 任何分布$p(x)$都可以由多个不同均值和方差的高斯模型进行加权和进行拟合。（类似于傅里叶定理：不同信号都可以由多个正弦信号去进行拟合一样）

假设$z$表示第几个高斯分布，则
$$p(x)={\int }_{z}p(z)p(x|z)dz$$
其中$p(z)$可以理解为第z个高斯分布的权值(概率分布)， $x|z\sim N({\mu }_z,{\Sigma }_z)$, 则$p(x|z)$为高斯分布。这是从混合高斯模型的角度来理解的VAE。

总结来说就是：我们要预测$p(x)$，但是模型很难直接预测出$p(x)$，因为分布未知并且分布复杂。但是我们可以通过预测很多个高斯分布去拟合$p(x)$。VAE就是先预测$p(z)$，再去预测$p(x|z)$，从而预测出最终目标。

1.2.2 隐空间角度理解以及ELBO（变分下界）

这个$z$又叫隐变量，为什么要用隐变量：我们可以理解为$p(x)$很难直接求出，但是我们可以先求$p(z)$，然后通过$p(z)$去求得$p(x)$，这样就方便多了，其中$p(z)$可以是任意我们自定义的分布，VAE中使用的是$p(z)=N(z;0,I)$。

我们可以通过边际化来表示$p(x)$
$$p(x)={\int }_{z}p(x,z)dz$$
又根据乘法公式：$p(x,z)=p(x)p(z|x)=p(z)p(x|z)$。根据贝叶斯公式，又有：
$$p(z|x)=\frac{p(x|z)p(z)}{p(x)}$$
其中$p(z|x)$叫后验概率； $p(x|z)$叫似然概率(通过z我们似乎可以预测出x)； $p(z)$叫先验概率(我们自定义)； $p(x)$叫证据（evidence）

根据最大似然理论，我们要极大化：
$$\begin{array}{rl}logp(x)& =log{\int }_z{p}_{\theta }(x,z)dz\\ & =log{\int }_z{q}_{\varphi }(z|x)\frac{p_{\theta }(x,z)}{q_{\varphi }(z|x)}dz\\ & =log{E}_{z\sim q_{\varphi }(z|x)}[\frac{p_{\theta }(x,z)}{q_{\varphi }(z|x)}]\\ & \ge E_{z\sim q_{\varphi }(z|x)}[log\frac{p_{\theta }(x,z)}{q_{\varphi }(z|x)}]\\ & ={\int }_z{q}_{\varphi }(z|x)log{p}_{\theta }(x,z)dz-{\int }_z{q}_{\varphi }(z|x)log{q}_{\varphi }(z|x)dz\\ & =E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x,z)]-E_{z\sim q_{\varphi }(z|x)}[log{q}_{\varphi }(z|x)]\\ & =L(q,\theta )\end{array}$$
其中：

• 第二行上下同乘一个数，结果不变；
• 第四行是根据詹森不等式；
• 我们称$L(q,\theta )$为ELBO（evidence lower bound，也是因为$p(x)$为evidence），我们可以i通过最大化ELBO，去近似最大化似然函数。

我们刚刚用乘法定理得到：$p(x,z)=p(x)p(z|x)=p(z)p(x|z)$，我们可以代入进去来看看ELBO的本质是什么：

1） 先代入$p(x,z)=p(x)p(z|x)$
$$\begin{array}{rl}L(q,\theta )& =E_{z\sim q_{\varphi }(z|x)}[logp(x)]+E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(z|x)]-E_{z\sim q_{\varphi }(z|x)}[log{q}_{\varphi }(z)]\\ & =E_{z\sim q_{\varphi }(z|x)}[logp(x)]-KL(q_{\varphi }(z|x)||p_{\theta }(z|x))\\ & =logp(x)-KL(q_{\varphi }(z|x)||p_{\theta }(z|x))\end{array}$$

所以我们可以得到（移位）：
$$logp(x)=L(q,\theta )+KL(q_{\varphi }(z|x)||p_{\theta }(z|x))$$
我们可以发现，当我们将最小化KL散度让其接近于0，也就是使得$q_{\varphi }(z|x)$与$p(z|x)$分布靠近，那么我们就等近似将对数似然看作是ELBO。而$q_{\varphi }$可以看作是encoder，我们使用NN来拟合$p_{\theta }(z|x)$

2） 代入$p(x,z)=p(z)p(x|z)$
$$\begin{array}{rl}L(q,\theta )& =E_{z\sim q_{\varphi }(z|x)}[logp(z)]+E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x|z)]-E_{z\sim q_{\varphi }(z|x)}[log{q}_{\varphi }(z|x)]\\ & =E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x|z)]-KL(q_{\varphi }(z|x)||p(z))\end{array}$$
其中第一项可以认为模型的decoder，既根据隐变量$z$得到$x$的概率分布对数似然最大化；第二项是最大化负的KL散度，既最小化KL散度，既使得$q_{\varphi }(z|x)$与$p(z)$更接近。这里可以认为我们希望encoder预测出来的$q_{\varphi }(z|x)$和我们自定义的$p(z)$越接近越好，此处KL散度相当于约束项。

至此我们可以发现ELBO的本质：（小小总结一下）

1. 由第一项我们可以知道，我们可以用$q_{\varphi }(z|x)$来替代$p(z|x)$，训练模型去拟合该分布，这样对数似然可以等价于ELBO。为什么要替代$p(z|x)$，因为根据隐空间角度，我们不好直接求$p(x)$，所以设置隐变量$p(x)={\int }_{z}p(z)p(x|z)dz$，我们用模型去拟合后一项。
2. 由第二项我们可以知道，ELBO实际包含了$p_{\theta }(x|z)$和$q_{\varphi }(z|x)$，正好对应了decoder和encoder，并且我们还要尽量让$q_{\varphi }(z|x)$去拟合$p(z)$，这也是一项约束项，否则我们只有重建损失（$E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x|z)]$）就变回AE了。

1.2.3 Encoder

VAE里假设$z$是一个高斯变量，那么后验分布$q_{\varphi }(z|x)$也是高斯分布，我们不知道的是均值和方差，那么我们只要让encoder去拟合均值和方差，我们便可以知道该后验分布了。既
$$q_{\varphi }(z|x)=N({\mu }_{\varphi }(x),{\Sigma }_{\varphi }(x))$$
从这里我们也可以看到，$x$对应的是一个高斯分布，而不是一个确定的$z$值。

那么我们是如何衡量拟合的好坏的呢，根据上边的ELBO式子，我们有：
$$L=E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x|z)]-KL(q_{\varphi }(z|x)||p(z))$$
也就是通过KL散度来衡量其与$p(z)$的拟合近似程度。
两个高斯分布的KL散度是有已知公式的，直接带入即可：
$$KL(N({\mu }_{\varphi },{\Sigma }_{\varphi })||N(0,1))=\frac{1}{2}({\sigma }_{\varphi }^2+{\mu }_{\varphi }-1-log{\sigma }_{\varphi }^2)$$

这也就是我们的分布约束项，直觉上来说，当${\mu }_{\varphi }=0，{\Sigma }_{\varphi }=1$时，该KL散度会最小。

参数重整化（Reparameterization Trick）

我们已知$z$是随机变量，既$z$是从分布$q_{\varphi }(z|x)$随机采样出来的，那么对于输入同一个$x$,可能每次采样的$z$都是不一样的，所以这样是不可以梯度反传的。
这里使用参数重整化，既用一个确定值和随机值来代替一整个随机值，看下图

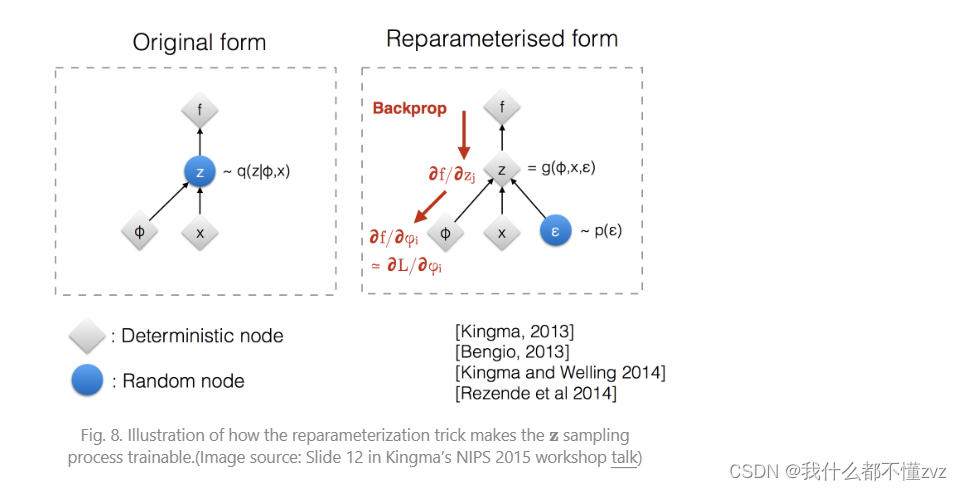
这里我们每次传入$x$都生成均值和方差，这是确定的（因为传入的x不变，通过NN函数拟合当然是确定的），这里我们从$N(0,1)$的正态分布中采样噪声，这是随机的，然后我们通过乘方差加均值的方法得到满足$N(\mu ,\Sigma )$的z，这样z就相当于从N(0,1)里采样，但是根据参数重整化得到与从后验概率分布中采样一样的道理，也就可以梯度反向传播了。

1.2.4 Decoder

同理，decoder输出的也是一个概率分布，最后输出的$X$是随机变量。这里我们同样也是通过预测均值和方差的方法来预测该概率分布，只不过VAE（大多数其他方法）会将方差固定为一个常数，所以用均值来等价于$X$。既
$${\mu }_x=decoder(z)$$

我们根据ELBO公式已知，优化目标为：
$$E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x|z)]$$
但是我们encoder输出的是概率分布而不是$Z$的具体数值，所以期望本身是不能解析的。我们可以借助马尔可夫链蒙特卡罗法（MCMC）去近似，既从后验概率中随机采样多个$\hat{z}$去近似等价：
$$E_{z\sim q_{\varphi }(z|x)}[log{p}_{\theta }(x|z)]\approx \frac{1}{L}\sum _{l=1}^L[log{p}_{\theta }(x|z^l)]$$
根据经验，$L=1$即可。

最终ELBO的式子：

1.3 VAE代码和细节实现

2 VQVAE

2.1 AE、VAE和VQVAE

已知AE由输入$x$，经过encoder得到确定值$z$，再经过decoder还原$x^{\prime }$，在编码过程中，$x、z$是唯一对应的，所以严格来说，AE并不是生成模型，而是一个数据压缩模型。

VAE就是对AE的一种改进，通过约束$z$满足正态分布，这样解码器就认得编码器编码出的向量，也就能实现生成任务。注意，AE和VAE生成的都是连续变量（这里的连续可以理解为他们都生成了概率分布，只不过AE生成的是概率分布中的某个样本点，而VAE就是生成一个概率分布）。

但是VAE生成的图像质量并不高，VQVAE的作者认为VAE不好的原因是因为编码器生成的连续变量，而如果生成的是离散变量那么生成的图像质量会更好。比如画一个人，他是男(0)或者是女(1)，我们可以用离散的向量进行编码，而不是连续向量(0.7为男，0.3为女）。

VQVAE采用NLP里的embedding的思想，embedding可以看作是特殊的连续向量，将编码器输出的变量$z$与嵌入空间(embedding space, codebook)使用K最邻近算法(距离使用均方根差，然后使用argmin找到与该向量距离最小的索引）找出最接近的嵌入向量索引，然后根据索引用该嵌入向量替代原来的编码器的输出。

现有的问题就是：

1. VAE约束$z$满足正态分布形式，VQVAE又尝试将$z$离散化，这样又会丢失掉编码空间的规范性，而离散化变量是不容易采样的，离散化后VQVAE不就不能生成图像了嘛？素嘟，VQVAE实际上是一个AE，只不过其编码出来的是离散的变量，VQVAE不是一个生成模型，他是一个图像压缩模型，而生成模型是其他的生成模型（pixelCNN、diffussion(构成stabe diffusion)等)

现在尝试理解以下问题：

• 如何输出离散变量？
• 如何优化encoder、decoder？
• 如何优化codebook（不是fixed，而是trainable的）

2.2 输出离散变量

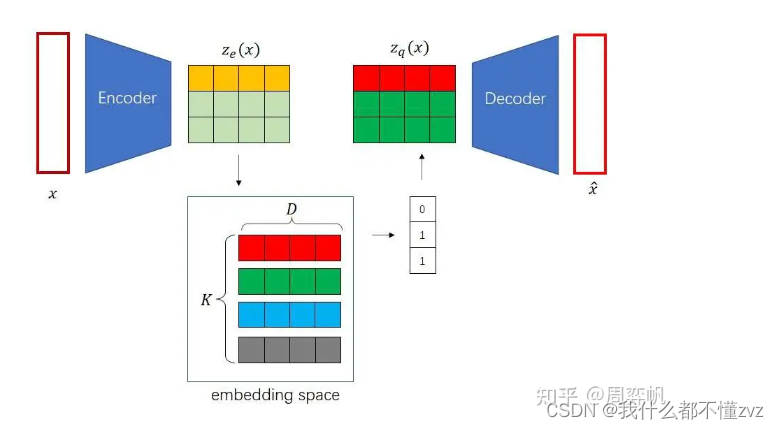
• 假设输入$x$为 [B,C,N,N], 编码器encoder的输出$z$为 [B,D,M,M] ,
• codebook的尺寸为 [K,D]，表示有K个嵌入向量，每个嵌入向量的维度为D。在计算距离时，先让$z$和codebook扩维（方便使用广播机制），既让$z$ 变为 [B,1,D,M,M], 而 codebook变为 [1,K,D,1,1], 然后使用均方根差计算距离，并在第二维（K）使用argmin 找到每个$z$ 对应嵌入向量最小距离的索引，然后得到索引之后我们就可以找到codebook中替代原编码输出的$z_q$了。
• 索引的尺寸为 [B,M,M] 既每个输出都对应一个嵌入向量索引，少了D维是因为这就是嵌入向量的深度。所以$z_q$的尺寸为 [B,D,M,M]

2.3 优化encoder和decoder

argmin是一个离散的操作，所以是不可导的。在AE中，我们的reconstrucion loss为：
$$L=||x-decoder(z)|{|}^2$$

VQVAE中变为：
$$L=||x-decoder(z_p)|{|}^2$$
而这项损失的梯度是不能传导到encoder的，因为$z$到$z_p$之间的变化是离散的。

VQVAE这里使用一种叫Straight-Through Estimator的方法，既设计函数：
$$L=||x-decoder(z-sg(z_p-z))|{|}^2$$
sg表示stop-gradient函数，在前向传播时为sg(x)=x，在反向传播时为0，也就是前向传播还是这么用，反向传播就不用了，直接把$z_p$求得的梯度去给encoder使用。
所以前向传播时： $x-decoder(z_p)$ ， 反向传播时 $L=||x-decoder(z)|{|}^2$

在pytorch中很容易实现：

l = x -  decoder(z - (zp-z).detach()) 

前面提到，codebook也是可训练的，那么codebook优化的目标是什么呢？ codebook优化的目标应该是： 尽可能使得codebook中的每一个嵌入向量都能尽可能表示编码器输出的每一类。比如【青年】这个的嵌入向量应该能表示14-48岁的所有编码器输出。

同样使均方根误差来计算，且使用sg函数将loss分成两部分，并配置不一样的权值（作者认为codebook应该学习的比encoder快，原论文参数为$\beta =1,\alpha =0.5$，实验可知，$\beta \in (0.1,2)$结果都差不多。
$$L_e=\beta ||sg(z)-z_p|{|}^2+\alpha ||z-sg(z_p)|{|}^2$$
第一项又叫VQ（vector quantisation)误差，主要作用是优化codebook；
第二项又叫专注（commitment)误差，主要作用是使encoder输出不要偏离codebook太远。

2.5 VQVAE代码细节

VQVAE本质上还是一个AutoEncoder。

模型上代码上新增的几个部分主要在于：

1. vq_embedding层： 使用nn.Embedding(n_embedding, dim) 作为codebook
2. encoder中要将输出的$z$ 与 vq_embedding的值进行均方距离的计算（算channel维度），得到[B,K,H,W]的距离矩阵，表示B*H*W个像素，每个像素对应codebook里的K个嵌入向量的距离，然后使用argmin找出距离最小的那个索引[B,H,W]。再将索引传入到vq_embedding进行运算，得到每个像素对应的嵌入向量的矩阵[B,H,W,D] (该D为嵌入向量的深度）
3. decoder中，输入到decoder的数据变为：z+(zq-z).detach()

训练过程新增的几个部分主要在于：

1. 三个损失： 重建损失mse_loss(x-x_hat)，embedding损失mse_loss(z.detach()-zq)，commitment损失mse_loss(z,zq.detach())

代码细节：

class VQVAE(nn.Module):

    def __init__(self, input_dim, dim, n_embedding):
        super().__init__()
        self.encoder = nn.Sequential(nn.Conv2d(input_dim, dim, 4, 2, 1),
                                     nn.ReLU(), nn.Conv2d(dim, dim, 4, 2, 1),
                                     nn.ReLU(), nn.Conv2d(dim, dim, 3, 1, 1),
                                     ResidualBlock(dim), ResidualBlock(dim))
        self.vq_embedding = nn.Embedding(n_embedding, dim)
        self.vq_embedding.weight.data.uniform_(-1.0 / n_embedding,
                                               1.0 / n_embedding)
        self.decoder = nn.Sequential(
            nn.Conv2d(dim, dim, 3, 1, 1),
            ResidualBlock(dim), ResidualBlock(dim),
            nn.ConvTranspose2d(dim, dim, 4, 2, 1), nn.ReLU(),
            nn.ConvTranspose2d(dim, input_dim, 4, 2, 1))
        self.n_downsample = 2

    def forward(self, x):
        # encode
        ze = self.encoder(x)

        # ze: [N, C, H, W]
        # embedding [K, C]
        embedding = self.vq_embedding.weight.data
        N, C, H, W = ze.shape
        K, _ = embedding.shape
        embedding_broadcast = embedding.reshape(1, K, C, 1, 1)
        ze_broadcast = ze.reshape(N, 1, C, H, W)
        distance = torch.sum((embedding_broadcast - ze_broadcast)**2, 2)
        nearest_neighbor = torch.argmin(distance, 1)
        # make C to the second dim
        zq = self.vq_embedding(nearest_neighbor).permute(0, 3, 1, 2)
        # stop gradient
        decoder_input = ze + (zq - ze).detach()

        # decode
        x_hat = self.decoder(decoder_input)
        return x_hat, ze, zq