BP/CNN神经网络总结整理

准备工作

常用的激励函数一般有两种，一种是sigmoid函数，它的值域为$(0,1)$，因此这个函数能很好地解释概率方面的意义。另一个函数是tanh函数，它的值域为$(-1,1)$。两个函数的形态都差不多，都是S型。

sigmoid函数的形式被定义为：
$$f(z)=\frac{1}{1+\exp (-z)}$$
其导数为
$$f^{\prime }(z)=f(z)(1-f(z))$$
tanh函数的形式被定义为：
$$f(z)=tanh(z)=\frac{\exp (z)-\exp (-z)}{\exp (z)+\exp (-z)}$$
其导数为：
$$f^{\prime }(z)=1-(f(z){)}^2$$

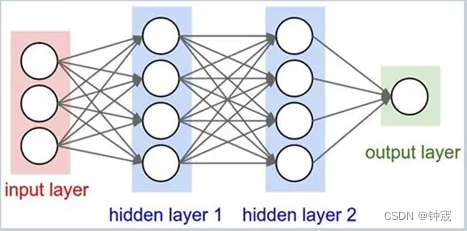
三层BP神经网络前向传导

这里说的三层，是指包含输入层、隐含层、输出层一共为三层。其前向传导可以用公式写为：
$$\begin{array}{rl}{a}^{(1)}& =x\\ z^{(2)}& =W^{(1)}{a}^{(1)}+b^{(1)}\\ a^{(2)}& =f(z^{(2)})\\ z^{(3)}& =W^{(2)}{a}^{(2)}+b^{(2)}\\ a^{(3)}& =f(z^{(3)})\end{array}$$
其中，x为输入特征，$a^{(1)}$为输入层。$W^{(1)}$和$b^{(1)}$为输入层到隐层映射时的参数。$z^{(2)}$是未被激活的隐层节点。$a^{(2)}$为激活了的隐层节点。$W^{(2)}$和$b^{(2)}$为隐含层到输出层映射的参数。$z^{(3)}$是未被激活的输出层节点。$a^{(3)}$为激活了的输出层节点。
如果不使用矩阵形式，那么可以写为：
$$\begin{array}{rl}{a}_i^{(1)}& =x_i\\ z_j^{(2)}& =\sum _i{W}_{ji}^{(1)}{a}_i^{(1)}+b_j^{(1)}\\ a_j^{(2)}& =f(z_j^{(2)})\\ z_k^{(3)}& =\sum _j{W}_{kj}^{(2)}{a}_j^{(2)}+b_k^{(2)}\\ a_k^{(3)}& =f(z_k^{(3)})\end{array}$$

其中，$i=1,2,...,N_i$,$j=1,2,...,N_h$,$k=1,2,...,N_o$。$N_i$,$N_h$,$N_o$分别表示输入层的节点数、隐含层层的节点数以及输出层的节点数。

代价函数

最为简单，也非常容易理解的单个样本的代价函数为：
$$J(W,b;x,y)=\frac{1}{2}\Vert h_{W,b}(x)-y{\Vert }^2$$
相应的全局代价函数为：
$$J(W,b)=\left[\frac{1}{m}\sum _{i=1}^{m}J(W,b;x^{(i)},y^{(i)})\right]+\frac{\lambda }{2}\sum _{l=1}^{n_l-1}\sum _{i=1}^{S_l}\sum _{j=1}^{S_{l+1}}(W_{ji}^l{)}^2$$

反向传播

为了优化全局函数，可以求梯度并进行迭代：
$$\begin{array}{rl}{W}_{ij}^{(l)}& =W_{ij}^{(l)}-\alpha \frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)\\ b_i^{(l)}& =b_i^{(l)}-\alpha \frac{\partial }{\partial b_i^{(l)}}J(W,b)\end{array}$$
也就是说，我们只要把注意力集中在求$J(W,b)$对$W_{ij}^{(l)}$和$b_i^{(l)}$的导数就可以了。
求导可得：
$$\begin{array}{rl}\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)& =\left[\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x^{(i)},y^{(i)})\right]+\lambda W_{ij}^{(l)}\\ \frac{\partial }{\partial b_i^{(l)}}J(W,b)& =\frac{1}{m}\sum _{i=1}^m\frac{\partial }{\partial b_i^{(l)}}J(W,b;x^{(i)},y^{(i)})\end{array}$$
OK。那么现在的问题全部集中在求解$\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x^{(i)},y^{(i)})$和$\frac{\partial }{\partial b_i^{(l)}}J(W,b;x^{(i)},y^{(i)})$上。

首先计算解$\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x^{(i)},y^{(i)})$。我们现在有：
$$\begin{array}{rl}J(W,b;x,y)& =\frac{1}{2}\Vert h_{W,b}(x)-y{\Vert }^2\\ & =\frac{1}{2}\sum _{k=1}^{N_o}(a_k^{(3)}-y_k{)}^2\end{array}$$
从这个式子中我们知道：
$$\frac{\partial J}{\partial a_i^{(3)}}=a_i^{(3)}-y_i$$
又，
$$a_i^{(3)}=f(z_i^{(3)})$$
所以，
$$\frac{\partial a_i^{(3)}}{\partial z_i^{(3)}}=f^{\prime }(z_i^{(3)})$$
又，
$$z_i^{(3)}=\sum _j{W}_{ij}^{(2)}{a}_j^{(2)}+b_k^{(2)}$$
所以，
$$\frac{\partial z_i^{(3)}}{\partial W_{ij}^{(2)}}=a_j^{(2)}$$
综合起来，就有：
$$\frac{\partial J}{\partial W_{ij}^{(2)}}=\frac{\partial J}{\partial a_i^{(3)}}\frac{\partial a_i^{(3)}}{\partial z_i^{(3)}}\frac{\partial z_i^{(3)}}{\partial W_{ij}^{(2)}}=(a_i^{(3)}-y_i)f^{\prime }(z_i^{(3)})a_j^{(2)}$$

下面再来推导$\partial J/\partial W_{ij}^{(1)}$。我们已知
$$J(W,b;x,y)=\frac{1}{2}\sum _{k=1}^{N_o}(a_k^{(3)}-y_k{)}^2$$
在这里，
$$\frac{\partial J}{\partial a_k^{(3)}}=\sum _{k=1}^{N_o}(a_k^{(3)}-y_k)$$
这是因为每一个$a_k^{(3)}，k=1,...,N_o$都是$W_{ij}^{(1)}$的函数。
$$\frac{\partial J}{\partial W_{ij}^{(1)}}=\frac{\partial J}{\partial a_k^{(3)}}\frac{\partial a_k^{(3)}}{\partial z_k^{(3)}}\frac{\partial z_k^{(3)}}{\partial a_i^{(2)}}\frac{\partial a_i^{(2)}}{\partial z_i^{(2)}}\frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}}$$
其中，
KaTeX parse error: No such environment: eqnarray* at position 8: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲*̲}̲ \frac{\partial…

归纳总结

推广一下，可以首先设定一个变量${\delta }_i^{(l)}$，其中$i$表示第单元的序号，$l$表示层数，它被定义为：
$${\delta }_i^{(l)}=\frac{\partial }{\partial z_i^{(l)}}J(W,b;x,y)$$
比如刚才的例子中，
$$\begin{array}{rl}{\delta }_i^{(3)}& =\frac{\partial }{\partial z_i^{(3)}}J(W,b;x,y)\\ {\delta }_i^{(2)}& =\frac{\partial }{\partial z_i^{(2)}}J(W,b;x,y)\\ & =\frac{\partial J}{\partial a_k^{(3)}}\frac{\partial a_k^{(3)}}{\partial z_k^{(3)}}\frac{\partial z_k^{(3)}}{\partial a_i^{(2)}}\frac{\partial a_i^{(2)}}{\partial z_i^{(2)}}\end{array}$$
定义了${\delta }_i^{(l)}$后，就有：
$$\begin{array}{rl}\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x,y)& =a_j^{(l)}{\delta }_i^{(l+1)}\\ \frac{\partial }{\partial b_i^{(l)}}J(W,b;x,y)& ={\delta }_i^{(l+1)}\end{array}$$
上式的证明是这样：
$$\begin{array}{rl}\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b;x,y)& =\frac{\partial J}{\partial z_i^{(l+1)}}\frac{\partial z_i^{(l+1)}}{\partial W_{ij}^{(l)}}\\ \frac{\partial }{\partial b_i^{(l)}}J(W,b;x,y)& =\frac{\partial J}{\partial z_i^{(l+1)}}\frac{\partial z_i^{(l+1)}}{\partial b_i^{(l)}}\end{array}$$
由于
$$z_i^{(l+1)}=\sum _k{W}_{ik}^{(l)}{a}_k^{(l)}+b_i^{(l)}$$
所以
$$\begin{array}{rl}\frac{\partial z_i^{(l+1)}}{\partial W_{ij}^{(l)}}& =a_j^{(l)}\\ \frac{\partial z_i^{(l+1)}}{\partial b_i^{(l)}}& =1\end{array}$$

向量化

刚刚的都是针对单个标量的公式求导。真正实现的时候，可以转换为向量形式：
$$\begin{array}{rl}{\mathbf{\delta }}^{(n_l)}& =-(\mathbf{y}-{\mathbf{a}}^{(n_l)})\bullet f^{\prime }({\mathbf{z}}^{(n_l)})\\ {\mathbf{\delta }}^{(l)}& =\left((W^{(l)}{)}^T{\mathbf{\delta }}^{(l+1)}\right)\bullet f^{\prime }({\mathbf{z}}^{(\mathbf{l})})\end{array}$$
则
$$\begin{array}{rl}{\nabla }_{W^{(l)}}J(W,b;x,y)& ={\mathbf{\delta }}^{(l+1)}{\left({\mathbf{a}}^{(\mathbf{l})}\right)}^T\\ {\nabla }_{b^{(l)}}J(W,b;x,y)& ={\mathbf{\delta }}^{(l+1)}\end{array}$$
另外，我们还可以使用下式来简化计算
$$f^{\prime }(z_i^{(l)})=f(z_i^{(l)})(1-f(z_i^{(l)}))=a_i^{(l)}(1-a_i^{(l)})$$

整体梳理

1. 令$\Delta W^{(l)}:=0$, $\Delta {\mathbf{b}}^{(l)}:=0$。
2. For $i$=1 to $m$
3. 计算${\nabla }_{W^{(l)}}J(W,b;x,y)$和${\nabla }_{b^{(l)}}J(W,b;x,y)$
4. 令$\Delta W^{(l)}:=\Delta W^{(l)}+{\nabla }_{W^{(l)}}J(W,b;x,y)$
5. 令$\Delta {\mathbf{b}}^{(\mathbf{l})}:=\Delta {\mathbf{b}}^{(l)}+{\nabla }_{b^{(l)}}J(W,b;x,y)$
6. 更新参数：
   $$\begin{array}{rl}{W}^{(l)}& =W^{(l)}-\alpha \left[(\frac{1}{m}\Delta W^{(l)})+\lambda W^{(l)}\right]\\ {\mathbf{b}}^{(l)}& ={\mathbf{b}}^{(l)}-\alpha \left[(\frac{1}{m}\Delta {\mathbf{b}}^{(l)})\right]\end{array}$$

最后一层变为softmax模型

如果使用softmax模型，则代价函数变为
J ( θ ) = − [ ∑ n = 1 N ∑ k = 1 K 1 { y ( n ) = k } l o g e x p ( ( θ ( k ) ) T h W , b ( x ( n ) ) ) ∑ j = 1 K e x p ( ( θ ( j ) ) T h W , b ( x ( n ) ) ) ] = − ∑ n = 1 N ∑ k = 1 K t n k log ⁡ S n k \begin{align} J(\theta) &= -\left[ \sum_{n=1}^N\sum_{k=1}^K1\{ y^{(n)}=k \}log\frac{exp\left(\left( \theta^{(k)} \right)^T h_{W,b}\left( x^{(n)} \right) \right)}{\sum_{j=1}^Kexp\left(\left( \theta^{(j)} \right)^T h_{W,b}\left( x^{(n)} \right) \right)} \right]\\ &= - \sum_{n=1}^N\sum_{k=1}^K t_{nk} \log S_{nk}\\ \end{align} J(θ)​=− ​n=1∑N​k=1∑K​1{y(n)=k}log∑j=1K​exp((θ(j))ThW,b​(x(n)))exp((θ(k))ThW,b​(x(n)))​ ​=−n=1∑N​k=1∑K​tnk​logSnk​​​
其中，
t n k = 1 { y ( i ) = k } S n k = exp ⁡ ( ( θ ( k ) ) T h W , b ( x ( n ) ) ) ∑ j = 1 K exp ⁡ ( ( θ ( j ) ) T h W , b ( x ( n ) ) ) \begin{align} t_{nk} &= 1\{ y^{(i)}=k \}\\ S_{nk} &= \frac{\exp\left(\left( \theta^{(k)} \right)^T h_{W,b}\left( x^{(n)} \right) \right)}{\sum_{j=1}^K\exp\left(\left( \theta^{(j)} \right)^T h_{W,b}\left( x^{(n)} \right) \right)}\\ \end{align} tnk​Snk​​=1{y(i)=k}=∑j=1K​exp((θ(j))ThW,b​(x(n)))exp((θ(k))ThW,b​(x(n)))​​​
在$S_{nk}$中，$n$表示的是样本的序列。不失一般性，去掉$n$，则有
$$P(y=k|x;\theta )=S_k(x;\theta )=\frac{\exp (z_k^{(3)})}{{\sum }_j\exp (z_j^{(3)})}$$
其中，
$$\begin{array}{rl}{z}_k^{(3)}& ={\left({\theta }^{(k)}\right)}^T{h}_{W,b}\left(x^{(n)}\right)\\ {\mathbf{a}}^{(2)}& =h_{W,b}\left(x^{(n)}\right)\end{array}$$
然后我们便可以根据之前所说的来求解${\delta }_i^{(3)}$。
$$\begin{array}{rl}{\delta }_i^{(3)}& =\frac{\partial J}{\partial z_i^{(3)}}\\ & =\frac{\partial J}{\partial S_{nk}}\frac{\partial S_{nk}}{\partial z_i^{(3)}}\\ & =-\sum _{n=1}^N\sum _{k=1}^K{t}_{nk}\frac{1}{S_{nk}}{S}_{nk}(I_{ki}-S_{ni})\\ & =-\sum _{n=1}^N\sum _{k=1}^K{t}_{nk}(I_{ki}-S_{ni})\\ & =-\sum _{n=1}^N\left(\sum _{k=1}^K{t}_{nk}{I}_{ki}-\sum _{k=1}^K{t}_{nk}{S}_{ni}\right)\\ & =-\sum _{n=1}^N\left(t_{ni}-S_{ni}\right)\end{array}$$
在上面的推导中，我们利用了${\sum }_k{t}_{nk}=1$。

CNN(Convolutional Neural Network)

还是假设三层网络。第一层是输入层，第二层是卷积后池化的隐含层，第三层是最后的输出层。第二层和第三层之间是全连接的。则：
$$\begin{array}{rl}{\delta }_i^{(2)}& =\frac{\partial J}{\partial z_i^{(2)}}\\ & =\frac{\partial J}{\partial z_k^{(3)}}\frac{\partial z_k^{(3)}}{\partial a_j^{(2)}}\frac{\partial a_j^{(2)}}{\partial z_i^{(2)}}\\ & =\sum _{k=1}^K{\delta }_k^{(3)}{W}_{kj}^{(2)}\frac{\partial a_j^{(2)}}{\partial z_i^{(2)}}\end{array}$$
现在的关键是$\partial a_j^{(2)}/\partial z_i^{(2)}$。
下面考虑一下物理意义：

1. ${\mathbf{a}}^{(1)}$是输入层，一般来说，是一幅二维的图像。
2. 用一个kernel对这幅图像进行卷积，并加上一个偏移量后，称之为${\mathbf{z}}^{(2)}$。
3. 对${\mathbf{z}}^{(2)}$激励，并池化后的结果称之为${\mathbf{a}}^{(2)}$

那么可以举一个例子：设${\mathbf{z}}^{(2)}$为一个$8\times 8$的矩阵且池化为原尺寸的$\frac{1}{2}\times \frac{1}{2}$。则，
$$a_1^{(2)}=\frac{1}{4}\left(f(z_1^{(2)})+f(z_2^{(2)})+f(z_9^{(2)})+f(z_{10}^{(2)})\right)$$
这样，我们就知道
$$\begin{array}{rl}\frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}& =\frac{1}{4}{f}^{\prime }(z_1^{(2)})\\ \frac{\partial a_1^{(2)}}{\partial z_2^{(2)}}& =\frac{1}{4}{f}^{\prime }(z_2^{(2)})\\ \frac{\partial a_1^{(2)}}{\partial z_9^{(2)}}& =\frac{1}{4}{f}^{\prime }(z_9^{(2)})\\ \frac{\partial a_1^{(2)}}{\partial z_{10}^{(2)}}& =\frac{1}{4}{f}^{\prime }(z_{10}^{(2)})\end{array}$$
而这就相当于对$a_1^{(2)}$上采样为$2\times 2$，并且将每一个值变为原来的1/4。然后再分别与对应的$z_j^{(2)}$的导数相乘。由于我也不会严格推导，因此，这里就直接给出答案：
$${\delta }_k^{(2)}=upsample\left({\left(W_k^{(2)}\right)}^T{\delta }_k^{(3)}\right)\bullet f^{\prime }(z_k^{(2)})$$
那么，如果是max-pooling呢？还是举刚才的例子：
$$a_1^{(2)}=\max \left(f(z_1^{(2)}),f(z_2^{(2)}),f(z_9^{(2)}),f(z_{10}^{(2)})\right)$$
这个导数怎么求？其实也不难，如果我们知道$f(z_1^{(2)}),f(z_2^{(2)}),f(z_9^{(2)}),f(z_{10}^{(2)})$中哪个值最大，那么对那个$z_i^{(2)}$的分量求导就是$f^{\prime }(z_i^{(2)})$而对其它的分量求导就是0。
这样的话，就相当于${\delta }_k^{(2)}$的式子不用改，而只需要更改$upsample$的含义就可以了。求平均的池化方法类似于把误差平分到每一个单元，而max-pooling方法的误差全部都放到某一个上采样后的单元上，其它单元全部设为0。

到现在，${\delta }^{(2)}$已经求解成功，但还没有结束。下面还需要求解$\partial z_i^{(2)}/\partial W_{mn}^{(1)}$。假设kernel是一个$3\times 3$的矩阵。并且可以写成：
$$\left(\begin{array}{rcl}{W}_{11}^{(1)}& W_{12}^{(1)}& W_{13}^{(1)}\\ W_{21}^{(1)}& W_{22}^{(1)}& W_{23}^{(1)}\\ W_{31}^{(1)}& W_{32}^{(1)}& W_{33}^{(1)}\end{array}\right)$$
则$z_1^{(2)}={\sum }_{i=1}^3{\sum }_{j=1}^3{W}_{ij}^{(1)}{a}_{ij}^{(1)}+b^{(1)}$
则$\partial z_1^{(2)}/\partial W_{11}^{(1)}=a_{11}^{(1)}$，而对$W_{11}^{(1)}$有贡献的${\mathbf{z}}^{(2)}$的分量还有很多，他们的导数构成了一下的矩阵：
$$\left(\begin{array}{rcl}{a}_{11}^{(1)}& \cdots & a_{16}^{(1)}\\ ⋮& \ddots & ⋮\\ a_{61}^{(1)}& \cdots & a_{66}^{(1)}\end{array}\right)$$
综上，可以得出
$$\frac{\partial J}{\partial W_{11}^{(1)}}=\left(\sum _{i=1}^6\sum _{j=1}^6{\delta }_{ij}^{(2)}{a}_{ij}\right)$$
这其实可以看成是一种相关的形式，最后，给出整体的梯度：
$$\begin{array}{rl}{\nabla }_{W_k^{(1)}}J(W,b;x,y)& =(a^{(1)})\ast \text{rot90}({\delta }_k^{(2)},2),\\ {\nabla }_{b_k^{(1)}}J(W,b;x,y)& =\sum _{r,c}({\delta }_k^{(2)}{)}_{r,c}.\end{array}$$

CNN变种(高效版)

上面介绍的CNN，在第一层到第二层之间发生的变化依次为：卷积->激活->池化。而更加高效的做法是，把顺序调整一下，顺序依次为：卷积->池化->激活。用数学公式来示意一下，即为：
第一种：
$$D(f(W{x}_{(r,c)}+b))$$
第二种:
$$f(D(W{x}_{(r,c)})+b)$$
说第二种更高效的原因在于：在降采样的矩阵上做一些操作，总比在原矩阵上做同样的操作要快一些。更何况，激励函数中总是会包含指数操作。如果在DSP上运算，特别是在定点的DSP上进行运算，指数操作总是越少越好。
针对高效版的求导过程，与之前的CNN求导过程差的不多。这里就不赘述。一点提示就是，针对第一种，我的$z^{(2)}$取的是$W{x}_{(r,c)}+b$,而对于高效版的第二种，我的$z^{(2)}$取的是$W{x}_{(r,c)}$。
推导的结果是：
$${\delta }_k^{(2)}=upsample\left({\left(W_k^{(2)}\right)}^T{\delta }_k^{(3)}\bullet f^{\prime }(d_k^{(2)})\right)$$
其中，$d_k^{(2)}$对应的是$D(W{x}_{(r,c)})+b$部分。可以看到，在求解${\delta }_k^{(2)}$的部分，第二种与第一种的区别是，第一种在前向传播的过程中是先激活，再降采样的。因此在求导的时候先上采样，再乘以激活函数的导数。而第二种在前向传播的过程中是先降采样，然后再激活的。因此在求导的时候，先乘以激活函数的导数，然后再上采样。
其它的都与第一种相同。

写在最后

在上述的推导过程中，为了更加具体地描述，我都具体地表明了采用的神经网络的结构。我采用的结构一般都为三层。但事实上，掌握了上述的方法之后，可以将层数扩展到任意层。这是因为对$W^{(l)}$和$b^{(l)}$的导数，就只与当层的${\mathbf{a}}^{(l)}$与后一层的${\mathbf{\delta }}^{(l+1)}$有关。通过从后往前的推导，我们总能求解出$W^{(l)}$和$b^{(l)}$的导数。这也是反向传播的含义。
另外，虽然我对我的数学没有很大的信心，但是，通过实际的验证，表明推导的都是正确的。这才有信心把推导的内容记录下来。