树状数组（超详细）

      树状数组(binary indexed tree，发明者Peter M.Fenwick 1994)，是一种设计新鲜的数组结构，它能够高效地获取数组中连续 k 个数的和。

        概括说，树状数组通常用于解决以下问题：

        数组A中的元素可能不断地被修改，怎样才能快速地获取连续几个数地和？

介绍

什么是树状数组？

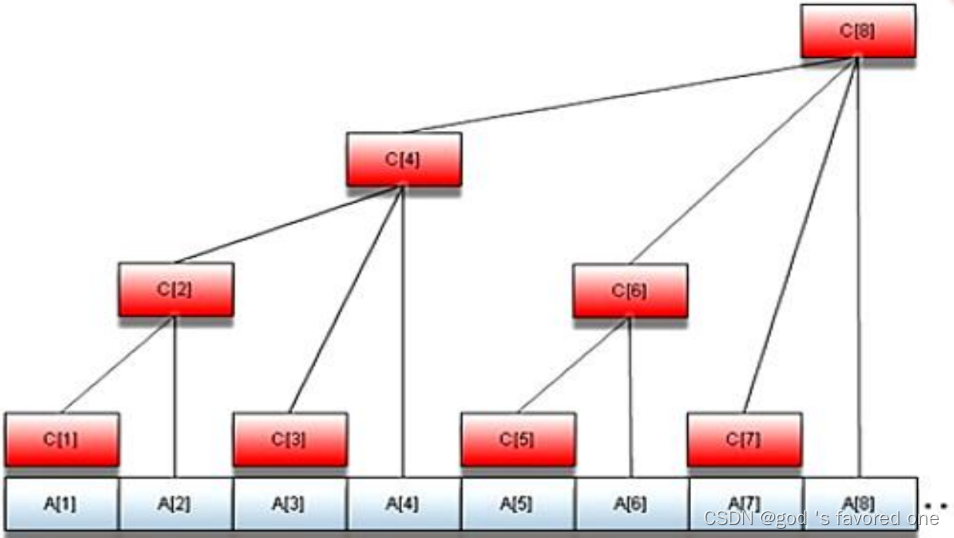
我们给定一个数组A[ ]，我们设一个数组C[ ]满足

……

那么C数组就是树状数组。

思考：

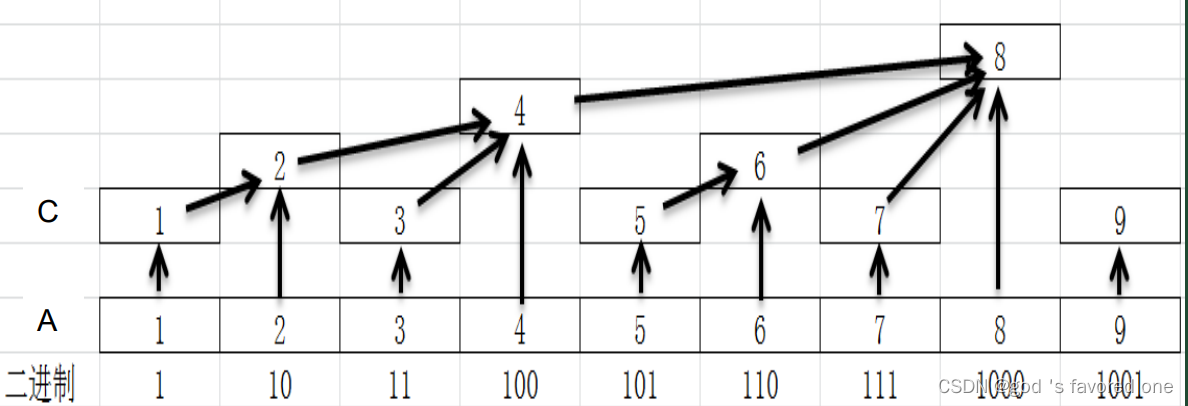
实际上，我们设  为（下标）对应二进制末位0的个数， 从  开始算！

那么：

那么，问题来了给定，如何求？

答案很简单： & 。

关于 & ：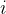

比如对于“010101000”最末有3个0， 的值应该是3，算出的应该为8

110101000    ->     这是-i的原码

101010111     ->     这是-i的反码

101011000     ->     这是-i的补码

010101000     ->     这是i的补码

000001000     ->     这是(i & (-i))

。

我们定义它为&。

c++简短函数代码：

int lowbit(int x){
    return x & (-x);
}

求和：

当我们求的之和时，

如果包含的不一定是的全部和，（比如）就需要再找一个（显然）累加起来，这个我们称之为的前驱，举个例子：

前驱的编号即为比自己小的，最近的，最末连续0比自己多的数

所以的前驱，相当于剪掉了自己最左边的1

求和函数：，代码如下：

int getSum(int x){
    int ans = 0;
    for(int i = x; i > 0; i -= lowbit(i)) ans += C[i];
    return ans;
}

直接用一个循环求得Sum，时间复杂度为。

求区间之和怎么办？

！

修改：

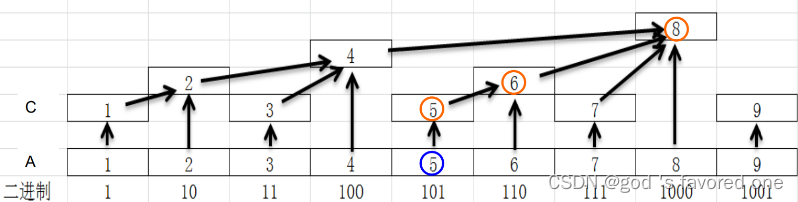
修改了某个 ，就需要改动所有包含的

从图上看就是要更改从叶子节点到根节点路径上所有的

怎么求一个节点的父节点？

经过观察和探究，前人们得出了这个规律：
父亲：比自己大的，最近的，末位连续0比自己多的数

节点父亲的编号

修改函数：

void modify(int x, int d){
    for(int i = x; i <= n; i += lowbit(i)) C[i] += d;
}

其时间复杂度依旧为

一个小小的问题：

那原本的数组，应该怎么做：

其实调用修改函数，相当于把没有修改为一个值，代码如下。

cin >> n;
for(int i = 1; i <= n; i++){
	cin >> x;
	modify(i, x);
}

小结：

1、在很多情况下，线段树都可以用树状数组实现，凡是能用树状数组实现的一定能用线段树。

2、当题目不满组减法原则的时候，就只能用线段树，不能用树状数组。

3、树状数组的时间复杂的每一个操作都是的时间复杂度。

这篇文章就在一个代码中结束了！

觉得博主写的不错的关注支持一下吧！我会继续努力的~