【知识点】（四）不定积分和定积分

不定积分

1. 概念和性质

• 概念：设 $F(x)$ 时 $f(x)$ 的一个原函数，则称 $f(x)$ 的所有原函数 $F(x)+C$ 为 $f(x)$ 的不定积分，记为 $\int f(x)dx$，即 $$\int f(x)dx=F(x)+C$$
• 性质：$$\frac{d}{dx}\int f(x)dx=f(x)，\int df(x)=\int f^{{}^{\prime }}(x)dx=f(x)+C$$

2. 基本公式

• $$\int x^{\alpha }dx=\frac{1}{\alpha +1}{x}^{\alpha +1}+C，\int \frac{1}{x^2}dx=-\frac{1}{x}+C，\int \frac{1}{\sqrt{x}}dx=2\sqrt{x}+C，\int \frac{1}{x}dx=\ln |x|+C$$

• $$\int \tan xdx=-\ln |\cos x|+C，\int \sec xdx=\ln |\sec x+\tan x|+C$$ $$\int {\sec }^{2}xdx=\tan x+C，\int \sec x\tan xdx=\sec x+C$$

• $$\int \frac{1}{a^2+x^2}=\frac{1}{a}arctan\frac{x}{a}+C，\int \frac{1}{a^2-x^2}dx=\frac{1}{2a}\ln |\frac{a+x}{a-x}|+C$$

• $$\int \frac{1}{\sqrt{a^2-x^2}}=\arcsin \frac{x}{a}+C，\int \frac{1}{\sqrt{x^2\pm a^2}}dx=\ln |x+\sqrt{x^2\pm a^2}|+C$$

3. 凑微分法

概念：设 $F(\varphi (x))$ 是 $f(\varphi (x))$ 的一个原函数，则 $$\int f[\varphi (x)]{\varphi }^{{}^{\prime }}(x)dx=\int f[\varphi (x)]d\varphi (x)=F(\varphi (x))+C$$

公式：

• $$\int f(ax+b)dx=\frac{1}{a}\int f(ax+b)d(ax+b)，\int \frac{1}{x}f(\ln x)dx=\int f(\ln x)d(\ln x)$$

• $$\int x^{n-1}f(a{x}^n+b)dx=\frac{1}{an}\int f(a{x}^n+b)d(a{x}^n+b)$$ $$特别地，\int \frac{1}{x^2}f(\frac{1}{x})dx=-\int f(\frac{1}{x})d(\frac{1}{x})，\int \frac{1}{\sqrt{x}}f(\sqrt{x})dx=2\int f(\sqrt{x})d(\sqrt{x})$$

• $$\int \frac{1}{1+x^2}f(\arctan x)dx=\int f(\arctan x)d\arctan x，\int \frac{1}{\sqrt{1-x^2}}f(\arcsin x)dx=\int f(\arcsin x)d\arcsin x，$$

4. 换元积分法

概念：设 $x=\varphi (t)$ 可导，$F(t)$ 是 $f[\varphi (t)]{\varphi }^{{}^{\prime }}(t)$ 的一个原函数，则 $$\int f(x)dx=\int f[\varphi (t)]d\varphi (t)=\int f[\varphi (t)]{\varphi }^{{}^{\prime }}(t)dt=F(t)+C=F({\varphi }^{-1}(x))+C$$

常用替换：

• 三角函数：
  $$\sqrt{a^2-x^2}，x=a\sin t；\sqrt{x^2+a^2}，x=a\tan t；\sqrt{x^2-a^2}，x=a\sec t$$ $$\sqrt{a{x}^2+bx+c}配方$$

• 倒代换：分母幂次比分子高出两次及以上，$t=\frac{1}{x}$

• 复杂函数直接代换：复杂函数如 $a^x,e^x,\ln x,\arcsin x,\arctan x，\sqrt[n]{}$，$t=复杂函数$

5. 分部积分法

概念：函数 $u=u(x),v=v(x)$ 具有连续的导数，且 $\int vdu$ 比 $\int udv$ 易求，则 $$\int udv=uv-\int vdu$$

• 函数求积难度从易到难顺序：
  $e^x=三角函数\sin >多项式P_n(x)>反三角函数\arcsin 和对数函数\ln$，函数相乘求积分，容易的设为 $v$，难求的设为 $u$，
• 前两项和多项式相乘 $P_n(x)$ 可用表格积分法：$\int (x^3+2x+6)e^{2x}dx$

$u$ 求导	$x^3+2x+6$	$3x^2+2$	$6x$	$6$	$0$
$v$ 积分	$e^{2x}$	$\frac{1}{2}{e}^{2x}$	$\frac{1}{4}{e}^{2x}$	$\frac{1}{8}{e}^{2x}$	$\frac{1}{16}{e}^{2x}$

$$\int (x^3+2x+6)e^{2x}dx=(x^3+2x+6)(\frac{1}{2}{e}^{2x})+(3x^2+2)(\frac{1}{4}{e}^{2x})+...+0\cdot (\frac{1}{16}{e}^{2x})+C$$

6. 有理函数积分

概念：有理函数可分为假分式和真分式，假分式拆分为多项式和真分式之和。真分式积分 $\int \frac{P_n(x)}{Q_m(x)}dx(n<m)$， 可先将 $Q_m(x)$ 因式分解，再根据 $Q_m(x)$ 的因式把$\frac{P_n(x)}{Q_m(x)}$ 拆分为若干有理分式之和

分解：

• $Q_m(x)$ 的一次因式 $(ax+b)$ 产生一项 $\frac{A}{ax+b}$
• $Q_m(x)$ 的 $k$ 重因式 $(ax+b{)}^k$产生一项 $\frac{A_1}{ax+b}+\frac{A_2}{(ax+b{)}^2}+...+\frac{A_k}{(ax+b{)}^k}$

求积：

• $\int \frac{A}{ax+b}dx=\frac{A}{a}\ln |ax+b|+C$
• $\int \frac{A_k}{(ax+b{)}^k}dx=-\frac{A_k}{a}\int \frac{1}{(ax+b{)}^k}d(ax+b)$

7. 三角函数积分

多项式：$\int {\sin }^{m}x{\cos }^{n}xdx$

• 若 $\sin x$ 和 $\cos x$ 次方至少一个为奇数，$\sin x$ 次方为奇数，$t=\cos x$；$\cos x$ 次方为奇数，$t=\sin x$
• 若 $\sin x$ 和 $\cos x$ 次方均是正偶数，$\sin x\cos x=\frac{1}{2}\sin 2x，{\sin }^{2}x=\frac{1-\cos 2x}{2}，{\cos }^{2}x=\frac{1+\cos 2x}{2}$
• 若 $\sin x$ 和 $\cos x$ 次方均是负偶数，$t=tanx$
• 若 $\sin x$ 和 $\cos x$ 次方分别是正偶数和负偶数，${\sin }^{2}x=1-{\cos }^{2}x$

分式：

• $$\frac{dx}{a\sin x+b}，\frac{dx}{a\cos x+b}，\frac{dx}{a\sin x+b\cos x+c}，t=\tan \frac{x}{2}$$

$$\sin x=2\sin \frac{x}{2}\cos \frac{x}{2}，\cos x={\cos }^2\frac{x}{2}-{\sin }^2\frac{x}{2}$$

• $$\int R(\sin x)\cos xdx，t=\sin x；\int R(\cos x)\sin xdx，t=\cos x；\int R({\sin }^{2}x,{\cos }^{2}x)dx，t=\tan x$$

定积分

1. 概念和性质

• 概念：设函数 $y=f(x)$ 在 $[a,b]$ 上有定义，在 $(a,b)$ 内任意插入 $n-1$ 个分点 $x_1,x_2,...,x_{n-1}$ 使得 $$a=x_0<x_1<x_2<...<x_n-1<x_n=b$$ 在第 $i$ 个小区间 $[x_{i-1},x_i]$ 任取一点 ${\xi }_i$，记 Δ x i = x i − x i − 1 ( i = 1 , 2 , . . . , n ) ， λ = m a x { Δ x 1 , Δ x 2 , . . . , Δ x n } \Delta x_i=x_i-x_{i-1}(i=1, 2, ..., n)，\lambda = max\{ \Delta x_1, \Delta x_2, ..., \Delta x_n\} Δxi​=xi​−xi−1​(i=1,2,...,n)，λ=max{Δx1​,Δx2​,...,Δxn​} $$\underset{\lambda \to 0}{\lim }\sum _{i=1}^{n}f({\xi }_i){\Delta }_i={\int }_a^{b}f(x)dx$$

• 性质：$${\int }_a^{b}f(x)dx=-{\int }_b^{a}f(x)dx，{\int }_a^{b}f(x)dx={\int }_a^{c}f(x)dx+{\int }_c^{b}f(x)dx$$

2. 定积分计算

• 牛顿-莱布尼茨公式：$${\int }_a^{b}f(x)dx=F(x){|}_a^b=F(b)-F(a)$$

• 换元积分法：从左到右是换元积分法，从右到左是凑微分法
  $${\int }_a^{b}f(x)dx={\int }_{\alpha }^{\beta }f({\varphi }^{{}^{\prime }}(t))\varphi (t)dt，$$

• 分部积分法：$${\int }_a^{b}udv=uv{|}_a^b-{\int }_a^{b}vdu$$

4. 计算工具

• 对称区间奇偶函数：$${\int }_{-a}^{a}f(x)dx=\{\begin{array}{ll}2{\int }_0^{a}f(x)dx& \text{f(x)偶函数}\\ 0& \text{f(x)奇函数}\end{array}$$

• 对称区间非奇偶函数：$${\int }_{-a}^{a}f(x)dx={\int }_0^a[f(x)+f(-x)]dx$$

• 周期函数：$${\int }_0^{nT}f(x)dx=n{\int }_0^{T}f(x)dx，{\int }_a^{a+T}f(x)dx={\int }_0^{T}f(x)dx，{\int }_T^{a+T}f(x)dx={\int }_0^{a}f(x)dx$$

• 积分区间 ${\int }_0^{\pi }$ 积分函数 $\sin x$
  $${\int }_0^{\pi }xf(\sin x)dx=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)dx=\pi {\int }_0^{\frac{\pi }{2}}f(\sin x)dx$$

$${\int }_0^{\pi }f(\sin x)dx=2{\int }_0^{\frac{\pi }{2}}f(\sin x)dx，{\int }_0^{\pi }\sin xdx=2$$

$${\int }_0^{\frac{\pi }{2}}f(\cos x)dx={\int }_0^{\frac{\pi }{2}}f(\sin x)dx，{\int }_0^{\frac{\pi }{2}}\cos xdx={\int }_0^{\frac{\pi }{2}}\sin xdx=1$$

$${\int }_0^{\frac{\pi }{2}}{\sin }^{n}xdx={\int }_0^{\frac{\pi }{2}}{\cos }^{n}xdx=\{\begin{array}{ll}\frac{n-1}{n}\cdot \frac{n-3}{n-2}...\cdot \frac{2}{3}& \text{n为奇数}\\ \frac{n-1}{n}\cdot \frac{n-3}{n-2}...\cdot \frac{1}{2}\cdot \frac{\pi }{2}& \text{n为偶数}\end{array}$$

• 区间再现公式 $x=a+b-t$：
  $$I={\int }_a^{b}f(x)dx={\int }_b^{a}f(a+b-t)(-dt)={\int }_a^{b}f(a+b-t)dt$$

原函数和可积

原函数：如果 $f(x)$ 在区间 $[a,b]$ 或 $(a,b)$ 上有任意一点 $F^{{}^{\prime }}(x)=f(x)$，则 $f(x)$ 在区间 $[a,b]$ 或 $(a,b)$ 有原函数。
可积：如果 $f(x)$ 在 $[a,b]$ 上的定积分存在，则 $f(x)$ 在 $[a,b]$ 上可积

原函数存在定理：连续、振荡间断点有原函数，可去、跳跃、无穷间断点无原函数。

可积：连续、有界且有限间断点、单调有界可积，无界不可积。

振荡间断点 $f(x)$ 存在原函数，有界可积
$$f(x)=\{\begin{array}{ll}2x\sin \frac{1}{x}-\cos \frac{1}{x}& x\ne 0\\ 0& x=0\end{array}$$

振荡间断点 $f(x)$ 存在原函数，无界不可积
$$f(x)=\{\begin{array}{ll}2x\sin \frac{1}{x^2}-\frac{2}{x}\cos \frac{1}{x^2}& x\ne 0\\ 0& x=0\end{array}$$

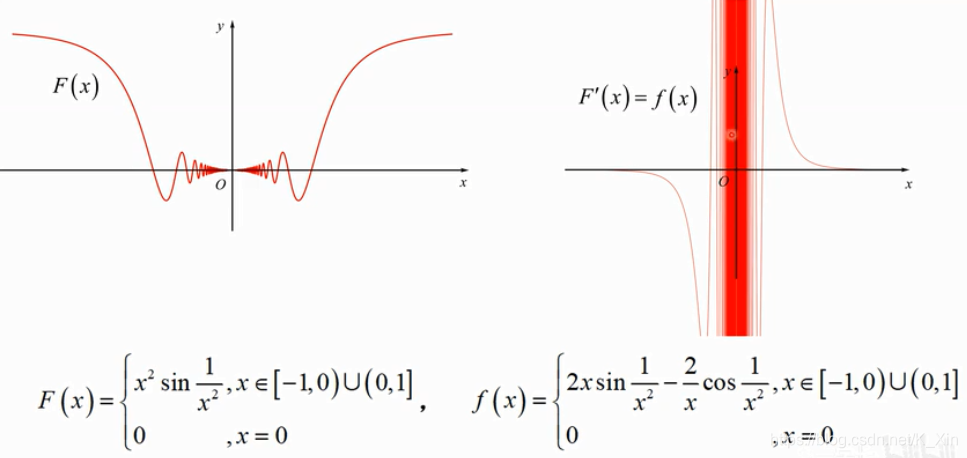
反常积分

1. 常用公式

2. 反常积分审敛法

找等价无穷小

当 $x\to 0$ 时，$1-\cos 3x$ ~ $\frac{9}{2}{x}^2$，$\sqrt[3]{\ln (1-x^2)}$ ~ $-x^{\frac{2}{3}}$，$\ln (\cos x)$ ~ $-\frac{1}{2}{x}^2$

当 $x\to \infty$ 时，$\frac{x}{\sqrt{x}(1+x^2)}$ ~ $\frac{x}{\sqrt{x}{x}^2}$ ~ $x^{-\frac{3}{2}}$；当 $x\to 1$ 时，$\ln x$ ~ $x-1$

无穷大和无穷小比较

当 $x\to 0$ 时， 无穷小按趋近于 $0$ 速度从快到慢排序： $x^2=1-{\cos }^{3}x>\sqrt[5]{x}>\frac{1}{\ln x}$

当 $x\to \infty$ 时， 无穷大按趋近于 $\infty$ 速度从快到慢排序： $e^x>x^2>\sqrt[3]{x}>{\ln }^{4}x$

当 $x\to 0$ 时，$\ln x$ 趋近于 $\infty$ 的速度比 $\frac{1}{x}$ 的任意正数次幂都慢

当 $x\to +\infty$ 时，$\ln x$ 趋近于 $\infty$ 的速度比 $x$ 的任意正数次幂都慢

参考资料

《微积分同步练习与模拟试题》刘强，孙激流
《张宇高等数学18讲》张宇
《数学复习全书》李正元，尤承业，范培华
戴方勤考研数学笔记
《8个题穷尽反常积分审敛法【附带习题和答案】》心一学长