电动汽车负荷预测+最优最优充放电最佳调度（Matlab代码）

     💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

电动汽车负荷预测与最优充放电调度研究综述

一、电动汽车负荷预测方法

二、最优充放电调度策略

三、负荷预测与调度的协同优化案例

四、挑战与未来方向

五、结论

📚2 运行结果

🎉3 参考文献 

🌈4 Matlab代码、数据下载

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

电动汽车负荷预测与最优充放电调度研究综述

一、电动汽车负荷预测方法

1. 确定性方法
   • 静态模型（EXP/ZIP）

• 优点：无需历史数据、计算成本低，适合评估EV基础影响。

  

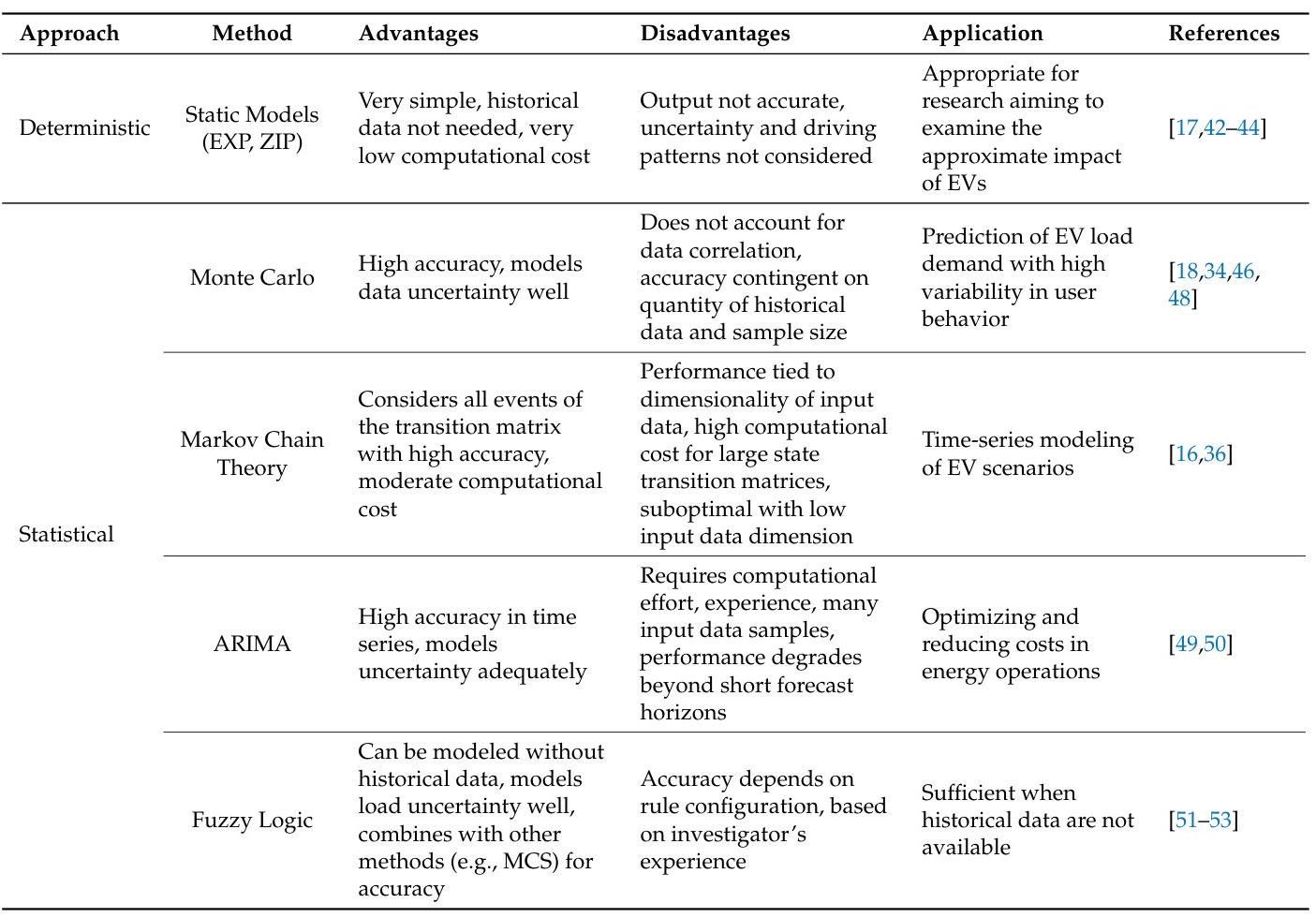
• 缺点：忽略不确定性及驾驶模式，精度有限，适用于宏观趋势分析。
• 应用案例：早期研究通过静态模型估算EV对电网的潜在负荷影响。

1. 统计学方法
   • 蒙特卡洛模拟（MCS）

• 核心思想：通过概率分布模拟用户行为（如出发时间、充电时长）。

• 改进方向：结合电池老化模型（如双离子电池寿命预测）与Bass回归分析EV保有量，提升预测精度。

• 案例：上海2015-2020年EV充电负荷预测显示，无序充电可能导致电网峰谷差增加10%-15%。

  • 马尔可夫链理论

• 优势：捕捉状态转移（如充电、放电、空闲），适合时间序列建模。

• 局限性：高维状态矩阵计算复杂度高，需简化应用场景。

  • ARIMA模型

• 适用性：短期时间序列预测，需大量历史数据支持。

• 问题：预测周期超过24小时后误差显著增加。

  • 机器学习方法

• LSTM网络：在动态负荷预测中表现优异，平均绝对误差（MAPE）较传统方法降低5%。

• FWA-BP混合模型：通过火炮算法优化神经网络参数，提升计算效率。

• 案例：基于卷积神经网络（CNN）的负荷预测模型，误差减少24倍。

1. 多因素融合模型
   • 考虑变量：用户行为（出行时间、里程焦虑）、环境因素（温度、节假日）、电池状态（SOC、老化）。
   • 创新模型：引入模糊逻辑处理不确定性，结合蒙特卡洛提升鲁棒性。

---

二、最优充放电调度策略

1. 目标函数设计

   • 电网侧：最小化峰谷差、负荷波动（日负荷均方差）。
   • 用户侧：降低充电成本、减少电池损耗、提升用户满意度（如SOC维持0.75-0.9）。
   • 协同目标：兼顾可再生能源消纳与电网稳定性。

2. 优化算法

   • 两阶段优化

• 第一阶段（计划调度） ：全局优化充放电计划与分时电价。

• 第二阶段（实时调整） ：基于实际偏差调整功率，限制充放电切换次数以延长电池寿命。

  • 智能算法

• 粒子群优化（PSO） ：用于动态电价策略与功率分配，收敛速度较快。

• 自适应遗传算法：优化充放电时间与功率，常温/极端环境下调度误差低于5%。

• NSGA-II多目标优化：生成Pareto解集平衡电网与用户利益。

1. 关键约束条件

   • 电池约束：充放电功率限制（如0.3C-1C）、SOC安全范围（20%-90%）。
   • 电网约束：节点电压偏差、线路载流量。
   • 用户心理效应：里程焦虑量化模型，通过滚动时域优化降低心理效应至0.25以下。

2. 调度策略类型

   • V2G技术：在负荷高峰期放电，低谷期充电，用户收益与电网削峰填谷双赢。
   • 分时电价引导：动态电价策略使充电成本降低10%-20%，同时平滑负荷曲线。
   • 集群调度：基于K-means分群，减少计算维度，提升实时响应速度。

---

三、负荷预测与调度的协同优化案例

1. 风光-EV协同调度

   • 模型设计：以日负荷均方差最小和充放电成本最低为目标，优化风电/光伏与EV充放电功率。
   • 效果：某区域电网峰谷差减少30%，可再生能源消纳率提升15%。

2. 城市配电网优化

   • 案例：南京理工大学研究结合出行链理论预测负荷，采用改进粒子群算法优化调度，用户成本降低18%，电网波动减少25%。
   • 技术细节：分布式控制架构分层优化，减少通信压力。

3. 长时间尺度调度

   • 策略：日前-实时双层模型，考虑电池损耗与用户心理效应，通过滚动优化维持高用户满意度。
   • 结果：调度周期内电池损耗成本降低12%，用户参与度提升40%。

---

四、挑战与未来方向

1. 数据驱动与不确定性建模

   • 问题：用户行为、天气等因素的随机性影响预测精度。
   • 解决方案：强化学习与数字孪生技术，实时更新预测模型。

2. 多目标协同优化

   • 研究方向：集成碳交易机制、需求响应与EV调度，提升综合能源系统经济性。

3. 电池健康管理

   • 创新点：动态调整充放电策略以平衡电网需求与电池寿命，如充放电切换次数限制。

4. 政策与市场机制

   • 建议：设计差异化电价与补贴政策，激励用户参与V2G。

---

五、结论

电动汽车负荷预测与充放电调度需结合统计学模型、智能算法与多因素协同优化。蒙特卡洛模拟与LSTM网络在预测中表现突出，而两阶段优化与自适应遗传算法在调度中效果显著。未来研究需进一步融合人工智能与市场机制，推动EV与电网的高效互动。

📚2 运行结果

部分代码：

% the charged load
N_Charged_Load=zeros(num_slot,3); % 1) the base load, 2) the charged load, 3) the total load (from EV rates), 
N_Charged_Load(:,1)=L_b_mic; % the base load
for i=1:num_slot
    for j=1:num_EV
        N_Charged_Load(i,2)=N_Charged_Load(i,2)+N_x_Matrix(j,i)*F(j,i);
    end
    N_Charged_Load(i,3)=N_Charged_Load(i,1)+N_Charged_Load(i,2); % total load calculated from charged loads of individual EVs
end


% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%  Plot the results %%%
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%  Plot the results %%%
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% plot the base load without EV charging
% load Glb_Chg_Load.txt;
figure;
xx=1:num_slot;
yy(:,1)=L_b_mic;  % the base load
yy(:,2)=v_Charged_Load(:,3); % globally optimal scheme
yy(:,3)=Charged_Load(:,3); %locally optimal scheme
yy(:,4)=N_Charged_Load(:,3); % Equal allocation scheme
plot(xx,yy);
ylabel('Load [KW]');
xlabel('Hour No.');
legend('Base load without EV charging','Total load with globally optimal EV charging','Total load with locally optimal EV charging','Total load with naive EV charging');

% conversion of charging rate matrix
G_x_Matrix_1D=reshape(v_x_Matrix', [], 1);  % globall optimal
L_x_Matrix_1D=reshape(x_Matrix', [], 1);  % locally optimal
N_x_Matrix_1D=reshape(N_x_Matrix', [], 1);  % naive

% the comparison of objective values    
obj_value=zeros(3,1);
obj_value(1)=k_0*sum(pow_p(yy(:,2),1)) + (k_1/2)*sum(pow_p(yy(:,2),2)) + beta*sum(square(F1)*square(G_x_Matrix_1D)) ...
        -k_0*sum(pow_p(L_b_mic(1:num_slot),1)) - (k_1/2)*sum(pow_p(L_b_mic(1:num_slot),2)); % total cost in globally optimal scheme
obj_value(2)=k_0*sum(pow_p(yy(:,3),1)) + (k_1/2)*sum(pow_p(yy(:,3),2)) + beta*sum(square(F1)*square(L_x_Matrix_1D)) ...
        -k_0*sum(pow_p(L_b_mic(1:num_slot),1)) - (k_1/2)*sum(pow_p(L_b_mic(1:num_slot),2)); % total cost in locally optimal scheme
obj_value(3)=k_0*sum(pow_p(yy(:,4),1)) + (k_1/2)*sum(pow_p(yy(:,4),2)) + beta*sum(square(F1)*square(N_x_Matrix_1D)) ...
        -k_0*sum(pow_p(L_b_mic(1:num_slot),1)) - (k_1/2)*sum(pow_p(L_b_mic(1:num_slot),2)); % total cost in Equal allocation scheme
    
imp_1=(obj_value(3)-obj_value(1))/obj_value(3);
imp_2=(obj_value(3)-obj_value(2))/obj_value(3);
fprintf('The objective value comparison: globally optimal scheme=%g, locally optimal scheme (group size %g) =%g, Equal allocation scheme=%g.\n',obj_value(1),group_size, obj_value(2),obj_value(3) );
fprintf('The improvement of the global optimal scheme is %g, the improvement of locally optimal scheme is %g.\n',imp_1, imp_2);


% plot the charged load in each interval
figure;
xx=1:num_slot;
zz(:,1)=v_Charged_Load(:,2); % globally optimal scheme
zz(:,2)=Charged_Load(:,2); %locally optimal scheme
zz(:,3)=N_Charged_Load(:,2); % Equal allocation scheme
plot(xx,zz);
ylabel('Charged load [KW]');
xlabel('Hour No.');
legend('Globally optimal scheme','Locally optimal scheme','Equal allocation scheme');


% the total charged energy
total_charged=0;
for i=1:num_EV
    total_charged=total_charged+ (Cap_battery-E_Charged(i,1));
end
fprintf('The total charged energy should be %g.\n',total_charged);
fprintf('The actual total charged energy:  globally optimal scheme=%g, locally optimal scheme=%g, Equal allocation scheme=%g.\n',...
    sum(yy(:,2)-yy(:,1)), sum(yy(:,3)-yy(:,1)), sum(yy(:,4)-yy(:,1)) );
    


% the load peak
Peak_based=max(L_b_mic); % the base load
Peak_Charged=max(Charged_Load(:,3)); % the load with EV charging
Peak_reduction=(Peak_based-Peak_Charged)/Peak_based;
fprintf('The peak comparison: base load=%g, globally optimal scheme=%g, locally optimal scheme=%g, Equal allocation scheme=%g KW.\n',...
    max(yy(:,1)), max(yy(:,2)), max(yy(:,3)), max(yy(:,4)) );

% the load standard deviation
std_based=std(L_b_mic); % the base load
std_Charged=std(Charged_Load(:,3)); % the load with EV charging
std_reduction=(std_based-std_Charged)/std_based;
fprintf('The standard deviation comparison: base load=%g, globally optimal scheme=%g, locally optimal scheme=%g, Equal allocation scheme=%g.\n',...
    std(yy(:,1)), std(yy(:,2)), std(yy(:,3)), std(yy(:,4)) );


fprintf('The number of the EVs is %g. The percentage of charging-only EVs is %g.\n', num_EV, P_Chg);

% plot the evolution of energy level for each EV (globally optimal scheme)
figure;
xxx=0:num_slot;
plot(xxx,v_Energy_variation(1:40,:));
ylabel('Energy [KWH]');
xlabel('Hour No.');
legend('EV1','EV2','EV3','EV4','EV5','EV6','EV7','EV8','EV9','EV10');
title('The energy evolution in globally optimal scheme');

% plot the evolution of energy level for each EV (locally optimal scheme)
figure;
xxx=0:num_slot;
plot(xxx,Energy_variation);
ylabel('Energy [KWH]');
xlabel('Hour No.');
legend('EV1','EV2','EV3','EV4','EV5','EV6','EV7','EV8','EV9','EV10');
title('The energy evolution in locally optimal scheme');

% plot the evolution of energy level for each EV (Equal allocation scheme)
figure;
plot(xxx,N_Energy_variation);
ylabel('Energy [KWH]');
xlabel('Hour No.');
legend('EV1','EV2','EV3','EV4','EV5','EV6','EV7','EV8','EV9','EV10');
title('The energy evolution in Equal allocation scheme');

% % plot the charging rates for each EV
figure; 
EV_ID=65;
energy_mmm(1,:)=v_Energy_variation(EV_ID,:);
energy_mmm(2,:)=Energy_variation(EV_ID,:);
energy_mmm(3,:)=N_Energy_variation(EV_ID,:);
plot(xxx,energy_mmm);
ylabel('Energy [KWH]');
xlabel('Time (Hours)');
legend('Globally optimal scheme','Locally optimal scheme','Equal allocation scheme');
title('The energy evolution for an EV');

figure;
nnn(:,1)=v_x_Matrix(EV_ID,:)';%globally optimal scheme
nnn(:,2)=x_Matrix(EV_ID,:)';%locally optimal scheme
nnn(:,3)=N_x_Matrix(EV_ID,:)';%Equal allocation scheme
h=bar(xx,nnn);
ylabel('Rate [KW]');
xlabel('Time (Hours)');
legend('Globally optimal scheme','Locally optimal scheme','Equal allocation scheme');
title('The charging/discharging rate in globally optimal scheme');

% save glabol_x_Matrix.txt v_x_Matrix -ascii;
% save local_x_Matrix.txt x_Matrix -ascii;
% save naive_x_Matrix.txt N_x_Matrix -ascii;

🎉3 参考文献 

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。(文章内容仅供参考，具体效果以运行结果为准)

[1]麻秀范,王超,洪潇,等.基于实时电价的电动汽车充放电优化策略和经济调度模型[J].电工技术学报, 2016, 31(A01):13.

[2]韩鹏.智能电网中电动汽车充电的优化调度研究[D].东北大学,2012.DOI:10.7666/d.J0118626.

[3]袁洁.电动汽车充放电变流与调度控制技术研究[D].湖南大学[2025-04-15]. 

🌈4 Matlab代码、数据下载

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取