运用物理信息神经网络求解流体力学方程

 01 

背景介绍

Navier-Stokes方程，作为流体力学中最有名的方程，是计算流体力学中最亟待解决的问题。在大多数情况下，Navier-Stokes方程都没有理论解析解，因此数值解成为解析流体问题的主要手段。在过去的几十年中，随着计算机技术和硬件的发展，计算流体力学也取得了巨大的进步。但是仍然有相当多的流体场景无法直接通过数值模拟计算得到，例如高雷诺数的湍流场景，复杂边界系统，多相流动等。因此现在有很多科学家通过另外一种途径来求解这些偏微分方程，那就是利用神经网络的推理能力和自动微分的特性，使其去近似方程的解。这种方法不需要像传统的求解过程一样在计算域中划分细密的网格，并且一旦完成对神经网络的训练，推理求解的过程将会十分迅速。

德国科学家Raissi等人[1，2，3]在2019年第一次提出了物理信息神经网络（PINNs）的概念，并且利用这种神经网络求解多种形式的偏微分方程的正向问题和反向问题。这种方法区别于数据驱动的方法，不需要大量的测量数据作为标签，在训练的过程中输入到神经网络中。这种方法同时也被运用到流体中层流，甚至是湍流的模拟中。因为流体中大面积的流场信息采集相当困难，直接数值模拟的方法也较难获得大量的数据。一个最基本，最核心的问题是，这种物理信息神经网络能否直接模拟湍流，就像使用高精度的直接数值模拟一样。

今年，哈尔滨工业大学李惠老师的课题组发表了一篇论文，实现了使用物理神经网络的方法对不可压缩流体的模拟。该论文同时研究了层流和湍流的问题，包括有二维的Kovasznay flow，圆柱绕流，三维的Beltrami flow，以及三维槽道湍流问题。除了纯粹的物理信息网络之外，论文中介绍了实际应用中使用的技巧，如自适应权重，自适应加密采样等。

 02 

算法介绍

下面让我们来看看具体的问题以及李惠老师课题组给出的解决方案。

图1 Navier-Stokes 方程

不可压缩流体的流动一般都可以用以上方程组描述。第一个方程代表了流体的动量守恒，也就是平时说的纳维-斯托克斯方程。第二个方程保证了流体的连续性，在一个点处流体的流进等于流出，即不可压缩流体。后面两项是边界条件，可以是狄利克雷边界条件或者是诺依曼边界条件。

图2 物理信息神经网络结构

论文中采用了全连接的神经网络，激活函数选用了tanh。如果是三维的场景，输入则是时间和空间的维度，输出是速度在空间三个方向上的分量和流场中每个点的压强。之所以称之为物理信息神经网络，是因为在神经网络中加入了有关物理方程的信息，这一部分体现在优化的损失函数上。在该论文中使用的是方程本身，初始和边界条件的残差，根据一定的权重来线性组合作为学习的损失函数。一般在训练过程中采用固定的权重，但是因为在训练过程中，各项残差的数值变化较大，所以固定权重经常会使其中一项占据主导，使其他几项无法得到很好的满足。论文作者在这里用到了动态权重的技巧，在训练过程使每一项损失项都保持在同一个量级上。

除了使用物理信息神经网络之外，论文中在采样上也增加了一个技巧。采样时，先对整个计算域内随机采样进行训练。然后随机收集Ne个点进行推理，计算损失函数，如果损失值大于某个设定值，则对损失值较大的地区增加采样点，直到损失值小于该设定的值。

部分结果展示

图3是论文中采用的圆柱绕流参考流场，源自德国慕尼黑工业大学的PhiFlow项目[4]通过直接数值模拟得到的结果。

图3 圆柱绕流计算参考样本

图4分别是固定边界和初始条件残差的权重为1和100以及采用了动态权重的模拟结果。

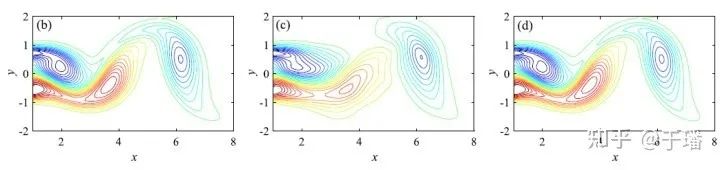
图4 物理信息神经网络得到的圆柱绕流结果

权重为100的结果精度较差，采用了动态权重的模拟结果比权重固定为1 的准确度提升了50%。

论文中首次使用了物理信息神经网络的方法去模拟湍流场景，下图是在一个三维槽道中较大雷诺数的湍流运动，参考数据来自约翰霍普金斯大学的公开数据库[5]。

图5 三维湍流中xy平面速度分布

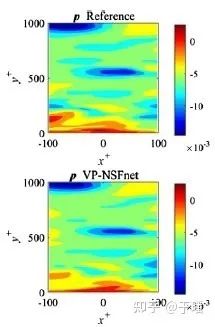
图6 三维湍流中xy平面压力分布

 03 

结论

目前物理信息神经网络可以应用于一些简单场景的流体运动推理模拟。论文中通过动态调整权重，采样方式等等优化技巧可以降低误差到1%以内。论文中还尝试了对于较大雷诺数的湍流模拟，是目前首次尝试使用湍流来评估物理信息神经网络的方法的性能表现。

这种方法的优点是需要较少的标签数据甚至不需要标签数据。但是目前存在泛化性的问题，更改方程的边界条件，初始条件，方程参数等等，需要重新训练模型。在论文的模型训练过程中，需要加入有监督的初始条件和边界条件以保证结果的准确性。如果采用纯粹的物理边界条件，该方法能否达到相同的精度还有待实验。下面附上原论文链接。

原论文链接：www.sciencedirect.com/science/article/pii/S0021999120307257?via%3Dihub

参考文献

[1] M. Raissi, P. Perdikaris, G.E. Karniadakis, Physics informed deep learning (part I): data-driven solutions of nonlinear partial differential equations, arXiv preprint, arXiv:1711.10561, 2017.

[2] M. Raissi, P. Perdikaris, G.E. Karniadakis, Physics informed deep learning (part II): data-driven discovery of nonlinear partial differential equations, arXiv preprint, arXiv:1711.10561, 2017.

[3] M. Raissi, P. Perdikaris, G.E. Karniadakis, Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, J. Comput. Phys. 378 (2019) 686–707.

[4]github.com/tum-pbs/PhiFlow

MindSpore官方资料

GitHub : https://github.com/mindspore-ai/mindspore

Gitee : https : //gitee.com/mindspore/mindspore

官方QQ群 : 486831414