各种距离(NOIP范围)

各种距离

（NOIP常用概念）

By Loi_Peacefuldoge

---

①欧几里德距离（euclidean metric）
亦被称之为欧几里得度量或欧氏距离
指在n维空间中两点的实际距离，或者是指向量的自然长度
（就是两点间的直线距离）
公式：|x| = √( x[1]^2 + x[2]^2 + … + x[n]^2 )
当然在NOIP我们常用的还是二维空间的公式
|x| = √( x[1]^2 + x[2]^2)
（勾股定理：Excuse me???）

②曼哈顿距离（Manhattan Distance）
曼哈顿距离又称出租车几何，是指两个点在标准坐标系上的绝对轴距总和
名称来源于在大城市中网格状的街道（类似就像纽约曼哈顿）走最短路，你不能斜着穿过建筑物，只能走直线，沿着平行于坐标轴的路径移动，显然是没有捷径的，因此就只有一种（以及它的各种投影们）
自行类比小学数学题……

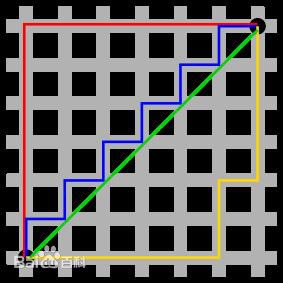
图中红线代表曼哈顿距离，绿线代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

③切比雪夫距离（Chebyshev distance）
就是指横纵距离中的较大值为这两点间的切比雪夫距离。
而数学上，切比雪夫距离（亦称L∞度量）是指向量空间中的一种度量，二个点之间的距离定义为其各座标数值差的最大值。
例如点(x1,y1)和点(x2,y2)，这两点间的切比雪夫距离为max(|x2-x1|,|y2-y1|)。
再举一个棋盘的例子
图示棋盘中，棋子从当前位置f6走到位置d4，（f6为1）则其切比雪夫距离为6。

---

THE END

其实本来还想写一些很强的东西（比如马氏距离），然而自己都看不明白TAT于是就放弃了这些对noip应该是够了