论文《SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks》

论文地址：https://arxiv.org/pdf/2006.10503.pdf

等变性

等变性（equivariance）指当输入进行某种变化的时候，输出进行相应的变化。完美的物体六维位姿估计具有对输入物体刚性变换（旋转和平移）的等变性，亦即如果对输入物体进行一个刚性变换，输出的位姿应也乘以这个刚性变换矩阵。在有标注的情况下，深度神经网络将依靠标注的引导进行位姿的学习，在训练良好的情况下，该网络近似满足等变性。当没有标注的时候，我们仍然需要获得等变的预测结果，而我们拥有的只有输入数据集，这样我们就考虑使用一个具有等变性的深度神经网络。

摘要

我们引入了SE(3)-Transformer，它是三维点云的自注意模块的一种变体，它在连续的三维旋转平动下是等变的。等变性对于确保在数据输入存在有害转换时的稳定和可预测的性能非常重要。 等变性 的一个积极的推论是增加了模型内的权重绑定，从而减少了可训练参数的数目，以此降低了样本的复杂性（即我们需要更少的训练数据）。SE(3)-Transformer利用自注意的好处，在具有不同数量点的大点云上操作，同时保证SE(3)-等变性的鲁棒性。我们在一个小N体粒子模拟数据集上评估我们的模型，展示了在输入旋转情况下预测的稳健性。

背景以及相关工作

一、自注意力机制（The Attention Mechanism）

假设有$n$个向量 { x i } i = 1 n \{x_i\}^n_{i=1} {xi​}i=1n​，${\alpha }_{ij}$相当于$x_i$和$x_j$的相关性。$Attn(Q,K,V)$，把注意力放在相关性更高的向量上。与CNN不同的是，CNN只考虑了一个卷积核内的相关性，而self-attention则考虑了全局的相关性。

排列等变性（Permutation equivariance）

self-attenton的一个关键性质是排列等变性。点标签$1、...，n$的排列导致了self-attenton输出的排列。这就保证了self-attenton的输出不会任意依赖于输入点的排序。瓦格斯塔夫等人，[30]最近表明，这种机制在理论上可以近似于所有的排列等变函数。SE(3)-Transformer是这种注意机制的一种特殊情况，继承了排列等变。然而，它限制了可学习函数的空间为旋转和平移等变函数

二、图神经网络（Graph Neural Networks）

Attention scales与点云大小呈二次关系，因此引入neighbourhoods是有用的：instead of each point attending to all other points, it only attends to its nearest neighbours（不需要关注每一个点，只需要关注它的邻居点）。
具有领域的几何被表示为图（graphs），并且 Attention很早就被引入到Graph。它具有简单的形式：

参考链接

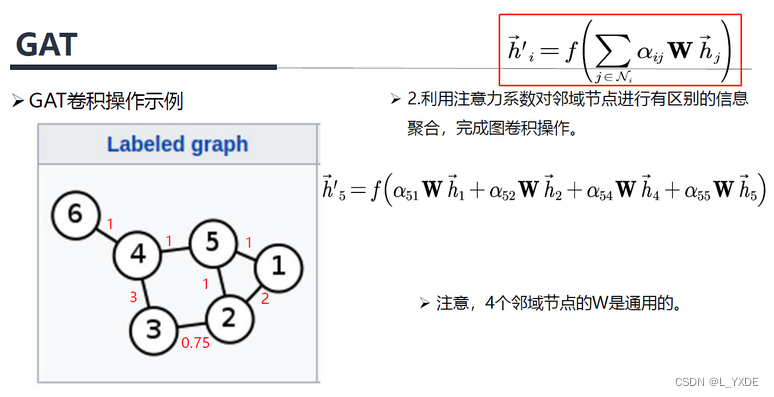
三、等变性（ Equivariance）

给定一对$(T_g，S_g)$，我们可以求解满足方程(4)的等变函数$\varphi$族。
在等变性文献中，深度网络是由交错线性映射$\varphi$和等变非线性建立的。在三维旋转平移的情况下，已经证明了一个适合$\varphi$的结构是一个张量场网络[25]，解释如下。请注意，Romero等人[21]最近引入了一个用于基于像素的图像数据的二维旋转平移等变注意模块。

Group Representations

一般来说，$(T_g，S_g)$称为group representations。
group representations $\rho :G\to GL(N)$是$G$到$N\times N$可逆矩阵$GL$的映射。更准确地说，$\rho$是group homomorphism，因此，它满足以下性质：$\rho (g_1{g}_2)=\rho (g_1)(g_2)$， $g_1,g_2\in G$
对于三维旋转$G=SO(3)$，有以下几个性质：
1）它的表示使正交矩阵；
2）它的表示可以分解为

其中$Q$是正交矩阵，$N\times N$的change-of-basis matrix（基的变换矩阵）。$D_l$是$(2l+1)\times (2l+1)$的Wigner-D矩阵。$\oplus$表示直和(direct sum)或沿着对角线矩阵连接。
Wigner-D矩阵是$SO(3)$的不可约表示(irreducible representations)——认为他们是可能的最小表示。

根据$D_l$(设置$Q=I,i=l$)变换的向量称为 type-l 向量。type-0 向量在旋转条件下保持不变，type-1向量根据三维旋转矩阵进行旋转。注意，type-l 向量的长度为$2l+1$。它们可以被堆叠起来，形成一个根据等式(5)变换的特征向量$f$

Tensor Field Networks

张量场网络(TFN)[28]是一种神经网络，它在SE(3)-equivariance约束下将点云映射到点云，即一组三维旋转和平移。对于点云，输入是形式如(6)的向量场 $f:R^3\to R^6$

$\delta$是 Dirac delta function， { x j } \{x_j\} {xj​}是3D点坐标， { f j } \{f_j\} {fj​}是点特征，表示原子序数或点身份。为了满足等变性，TFN变换的特征基于Eq(5)，其中$Q=I$。每个$f_i$是不同types向量的串联，type-l的子向量被写成$f_j^l$。
TFN层从type-k特征到type-l特征计算空间中连续的、可学习的权值核$W^{lk}:R^{(2l+1)\times (2k+1)}$。位置$x_i$的TFN层的type-l输出为：

$W^{lk}$位于等变基 { W J l k } J = ∣ k − l ∣ k + l \{W^{lk}_J\}^{k+l}_{J=|k-l|} {WJlk​}J=∣k−l∣k+l​的范围内。核是基础核的线性组合，其中半径$||x||$的第$J$个系数是一个可学习的函数${\phi }_J^{lk}:R_{\ge 0}\to R$。数学形式为
每一个基础核$W_J^{lk}:R^3\to R^{(2l+1)\times (2k+1)}$是由大小为$(2l+1)\times (2k+1)$的ClebschGordan matrices $W_{Jm}^{lk}$的线性组合形成的，其中第$Jm$个线性组合的系数是第$J$个球谐函数(spherical harmonic)$Y_J:R^3\to R^{2J+1}$的第$m$维。
每一个基础核$W_J^{lk}$约束在 angular direction上学习核的形式，在 radial direction上留下唯一可学习的自由度。注意，只有当$k\ne l$且$J=0$时，$W_J^{lk}(0)\ne 0$，这将核简化为一个标量$w$乘以恒等式，$W^{ll}=w^{ll}I$，称为$self-interaction$，这样就可以将TFN改写为：

等式(7)和等式(9)以消息传递的形式表示卷积，其中消息从所有节点和特征类型聚合。它们也是等式(3)中非局部图运算的一种形式，其中权值是边上的函数，特征 { f i } \{f_i\} {fi​}是节点特征。

方法

在这里，我们提出了SE(3)-Transformer。该层可以分解为如图2所示的步骤过程，我们将在下一节中描述。这些就是从点云构造图，构造图上的等变边函数，如何传播 图上的SE(3)-equivariance消息，以及如何聚合它们。我们还引入了自我交互层的另一种选择，我们称之为注意力自我交互(attentive self-interaction)。

Figure2： 用我们的等变注意机制更新节点特征分四个步骤。附录中提供了更详细的描述，特别是对步骤2的描述。步骤3和步骤4将图形网络视角可视化:特征从节点传递到边，以旋转等变的方式计算键、查询和值，这些都依赖于特征和相对位置。

3.1 Neighbourhoods

给定点云$\{(x_i,f_i)\}$，我们首先引入一个邻居 N i ⊆ { 1 , . . . , N } \mathcal{N}_i\subseteq\{1,...,N\} Ni​⊆{1,...,N}的集合，以每个点$i$为中心。这些邻域要么通过最近的邻域方法计算，要么已经定义了。例如，分子结构的邻域是由它们的键合结构确定的。邻域将注意力机制的计算复杂度从点数的二次型降低到线性型。邻域的引入将点云转化为图。该步骤如图2中的步骤1所示。

3.2 The SE(3)-Transformer

SE(3)-Transformer本身由三个组件组成:

1. edge-wise attention weights ${\alpha }_{ij}$ , constructed to be SE(3)-invariant on each edge $ij$,
2. edge-wise SE(3)-equivariant value messages,propagating information between nodes, as found in the TFN convolution of Eq. (7)
3. a linear/attentive self-interaction layer.
   

3.3 Node and Edge Features

4 A Group Theory and Tensor Field Networks

4.1 Groups

群是一个抽象的数学概念。形式上，一个群$(G,\circ )$由一个集合$G)$和一个二进制组合运算符$\circ :G\times G\to G$组成（通常我们只使用符号$G$来表示群）。所有的群都必须遵守以下4个公理：

封闭性：任意$g,h\in G$，满足$g\circ h\in G$
结合律：任意$g,h,f\in G$，满足$g\circ (h\circ f)=(g\circ h)\circ f$
幺元：任意$g\in G$，存在$e\in G$，使得$g\circ e=e\circ g$
逆元：任意$g\in G$，存在$g^{-1}\in G$，使得$g\circ g^{-1}=g^{-1}\circ g$

4.2 Actions/Transformations

用群描述变换，$T_g:X\to X$是一个自身到自身的变换。

举例：$x\in X,T_g(x)=gx+g,g\in G=1,2,3$，则$T_1(x)=x+1,T_2(x)=2x+2,T_3(x)=3x+3$

4.3 Equivariance and Intertwiners

给定两组变换：
$T_g:X\to X,g\in G$
$S_g:Y\to X,g\in G$
函数$f:X\to Y$
如果$S_g[f(x)]=f(T_g[x])$，则称$f$对$g$是等变的。

$T_g$和$S_g$是不同的变换，但他们的参数都由$g$决定。比如：$T_g(x)=gx+g$和$S_g=gy$。

放在本文中，可以将$x$看做输入点云的特征，$Tg$看成对$x$施加一个参数为$g$的变换；$f$表示对$x$提取特征，$Sg$看成施对$y$施加一个参数为$g$的变换

如果映射$f$是线性的和等变的，则称之为Intertwiners

现提出两个问题：
1）如何选择$S_g$
2）已知$(T_g,S_g)$如何求解$f$？
回答这些问题，需要了解群表示

4.4 Representations

$GL(V)$是一个可逆线性变换群，$v\in GL(V)$，说明$v$是一个可逆矩阵。
A group representation $\rho :G\to GL(V)$，如果$\rho (g_1,g_2)=\rho (g_1)\rho (g_2)$，则称群表示$\rho$是群$G$到群$GL(V)$的同态映射（简称同态），也称$\rho$是$G$的一个线性表示，$V$为表示空间。

如果${\rho }^{\prime }(g)=Q^{-1}\rho (g)Q,g\in G$，则$\rho$与${\rho }^{\prime }$等价(equivalent)

等价的表示：
在表示中，如果相同维数的两个表示$\rho$和${\rho }^{\prime }$可以通过相似变换连接，则称为等价的。可以想象线性空间中的不同的两组基，$Q$相当于两个基的过渡矩阵。说明$A$和$B$是同一个变换在不同基的表示

除了三维旋转矩阵，$SO(3)$ 群具有多种表示
我们也说一个群表示是可约的，如果它可以写成
$$\rho (g)={\mathbf{Q}}^{-1}\left({\rho }_1(g)\oplus {\rho }_2(g)\right)\mathbf{Q}={\mathbf{Q}}^{-1}\left[\begin{array}{cc}{\rho }_1(g)& \\ & {\rho }_2(g)\end{array}\right]\mathbf{Q},\text{ for all }g\in G$$

如果群表示${\rho }_1$和${\rho }_2$是不可约的，那么它们被称为$G$的不可约群表示。从某种意义上说，它们是表征之间的原子，所有其他表征都可以由它们构成。注意，每个不可约群表示作用于一个单独的子空间，将该空间的向量映射回子空间。我们说子空间${\mathcal{X}}_{\ell }\in \mathcal{X}$在不可约群表示${\rho }_{\ell }$下是不变的，如果 { ρ ℓ ( g ) x ∣ x ∈ X ℓ , g ∈ G } ⊆ X ℓ \left\{\rho_{\ell}(g) \mathbf{x} \mid \mathbf{x} \in \mathcal{X}_{\ell}, g \in G\right\} \subseteq \mathcal{X}_{\ell} {ρℓ​(g)x∣x∈Xℓ​,g∈G}⊆Xℓ​

4.5 Representation theory of SO(3)

群$SO(3)$的群表示理论表明，所有紧致群线性群表示都可以分解为不可约群表示的直和，如

$$\rho (g)={\mathbf{Q}}^{\top }\left[\underset{J}{⨁}{\mathbf{D}}_J(g)\right]\mathbf{Q},$$

其中$\mathbf{Q}$是一个正交矩阵，$N\times N$，基的变换矩阵

$Q$相当于两个基的过渡矩阵

每个${\mathbf{D}}_J$ for $J=0,1,2,\dots$是一个$(2J+1)\times (2J+1)$矩阵，称为Wigner-D矩阵。

Wigner D-矩阵就是卷积过程中SO(3)群的基底，相当于基础的傅里叶变换中的sin 和cos

Wigner-D矩阵是$SO(3)$的不可约表示。根据${\mathbf{D}}_J$(即我们设置$\mathbf{Q}=\mathbf{I}$)变换的向量称为type- $J$向量。

如：
4阶方阵 $\rho (g)$ 对4维向量的作用，分解成1阶方阵 $D_0(g)$ 对1维向量和3阶方阵 $D_1(g)$ 对 3 维向量的作用。
$$\begin{array}{c}\rho (g)\left(\begin{array}{l}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right)\to \left(\begin{array}{c}{v}_1^{\prime }\\ v_2^{\prime }\\ v_3^{\prime }\\ v_4^{\prime }\end{array}\right)\\ \left(\begin{array}{cc}{D}_0(g)& 0\\ 0& D_1(g)\end{array}\right)\left(\begin{array}{l}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right)=\left(\begin{array}{c}{D}_0(g)\left(\begin{array}{c}{v}_1\end{array}\right)\\ D_1(g)\left(\begin{array}{c}{v}_2\\ v_3\\ v_4\end{array}\right)\end{array}\right)=\left(\begin{array}{c}{l}_0\\ l_1\end{array}\right)\end{array}$$
从而把高维的表示分解成低维的表示。
其中$l_0$称为type-0向量，$l_1$称为type-1向量。

type-0向量在旋转下是不变的，type-1向量根据$3\mathrm{D}$旋转矩阵旋转。注意，type- $J$的向量长度为$2J+1$。
在上一段中，我们提到了不可约群表示作用于正交子空间${\mathcal{X}}_0,{\mathcal{X}}_1,\dots$。与Wigner-D矩阵对应的正交子空间是球谐空间。

4.6 The Spherical Harmonics

球谐函数$Y_J:S^2\to C^{2J+1}$是球面$S^2$上的平方可积复值函数
$$Y_J(R_g^{-1}x)=D_J^{\ast }(g)Y_J(x),x\in S^2,g\in G$$
$D_J$是第$J$个Wigner-D matrix，$D_J^{\ast }$是它的共轭

使用说明
球面坐标系的一点$P=(\theta ,\varphi )$，它的球谐函数值为$Y_J(P)$。现在对$P$施加一个旋转变换，假设旋转之后的坐标为$P^{\prime }=({\theta }^{\prime },\varphi \prime )$，那么它的球谐函数值为$Y_J(P^{\prime })$，并且此时满足$Y_J(P^{\prime })=D_J^{\ast }(g)Y_J(P)$。说明在对原数据施加旋转变换后，它的球谐函数值相当于是原来的球谐函数值乘以一个$D_J^{\ast }(g)$，这与我们构造一个等变权重$W$的目标使一致的。

我们可以将$L^2(S^2)$中的任何函数表示为球面谐波的线性组合：
$$f(x)=\sum _{J⩾0}{f}_J^T{Y}_J(x),x\in S^2$$
其中$f_J$是长度为$2J+1$的系数，$f_J={\int }_{S^2}f(x)Y_J^{\ast }(x)dx$

与傅里叶变换相似，$Y_J$相当于$\sin ,\cos$，$f_J$是系数

最重要的是，我们可以将旋转后的函数表示为：
$$f(\rho (g{)}^{-1}x)=\sum _{J⩾0}{f}_J^T{D}_J^{\ast }(g)Y_J(x),x\in S^2,g\in G$$

4.7 The Clebsch-Gordan Decomposition

Clebsch-Gordan coefficients被用于构造等变核。
它研究的是两个不可约表示的张量积如何分解成不可约表示的直和
分解形式如下：
$$D_k⨂D_g(g)={Q^{lk}}^T\left[\underset{J=|k-l|}{\overset{k+l}{⨁}}{D}_J(g)\right]Q^{lk}$$
在这个特定的情况下，基矩阵$Q^{lk}$的变化被赋予Clebsch-Gordan系数的特殊名称

4.8 Tensor Field Layers

张量场网络(TFN)是一种神经网络，它在SE(3)等变性条件下将点云映射到点云。
对于点云，输入是矢量场$f:{\mathbb{R}}^3\to {\mathbb{R}}^d$，其形式为：
$$f(x)=\sum _{j=1}^N{f}_j\delta (x-x_j)$$

相当于$f(x_i)=f_i$

式中 $\delta$ 为Dirac函数, { x j } \left\{\mathbf{x}_j\right\} {xj​} 为 $3\mathrm{D}$ 点坐标， { f j } \left\{f_j\right\} {fj​} 为点特征，且$f_j$由不同的tpye串联组成， $f_j$ 的type-$\ell$特征记为 $f_j^{\ell }$
$f_j^{\ell }$的长度为$2l+1$

假设$d=4$,则
$$f_j=\left(\begin{array}{c}{v}_0\\ v_1\\ v_2\\ v_3\end{array}\right)=\left(\begin{array}{c}{f}_j^0\\ f_j^1\end{array}\right)$$
其中$$f_j^0=\left(v_0\right),f_j^1=\left(\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right)$$

从$k$型特征到$\ell$型特征的可学习的系数核为： ${\mathbf{W}}^{\ell k}:{\mathbb{R}}^3\to {\mathbb{R}}^{(2\ell +1)\times (2k+1)}$

记$f_{in}^k(x)={\sum }_{j=1}^N{f}_{in,j}^k\delta (x-x_j)$，现在对$f_{in}^k(x)$和$W^{\ell k}(x)$求卷积：
$$\begin{array}{rl}{f}_{out,i}^{\ell }& =W^{\ell k}(x_i)\otimes f_{in}^k(x_i)\\ & =[W^{\ell k}\ast f_{in}^k](x_i)\\ & ={\int }_{{\mathbb{R}}^3}{W}^{\ell k}(x^{\prime }-x_i)f_{in}^k(x^{\prime })d{x}^{\prime }\\ & ={\int }_{{\mathbb{R}}^3}{W}^{\ell k}(x^{\prime }-x_i)\sum _{j=1}^N{f}_{in,j}^k\delta (x^{\prime }-x_j)d{x}^{\prime }\\ & =\sum _{j=1}^N{\int }_{{\mathbb{R}}^3}{W}^{\ell k}(x^{\prime }-x_i)f_{in,j}^k\delta (x^{\prime }-x_j)d{x}^{\prime }\\ & =\sum _{j=1}^N{W}^{\ell k}(x_j-x_i)f_{in,j}^k\end{array}$$
其中${\mathbf{W}}^{\ell k}(x)\in {\mathbb{R}}^{(2\ell +1)\times (2k+1)}$，$f_{in,j}^k\in {\mathbb{R}}^{(2k+1)}$，$f_{out,i}^{\ell }\in {\mathbb{R}}^{(2\ell +1)}$

上述推导是在一层tpye-$k$上，实际上，$f_j$由不同的tpye串联组成
因此，张量场网络在$x_i$处的type-$\ell$特征为：
$${\mathbf{f}}_{\mathrm{out},i}^{\ell }=\sum _{k\ge 0}\underset{k\to \ell \text{ convolution }}{\underbrace{\int {\mathbf{W}}^{\ell k}\left({\mathbf{x}}^{\prime }-{\mathbf{x}}_i\right){\mathbf{f}}_{\mathrm{in}}^k\left({\mathbf{x}}^{\prime }\right)\mathrm{d}{\mathbf{x}}^{\prime }}}=\sum _{k\ge 0}\sum _{j=1}^n\underset{\text{node }j\to \text{ node }i\text{ message }}{\underbrace{{\mathbf{W}}^{\ell k}\left({\mathbf{x}}_j-{\mathbf{x}}_i\right){\mathbf{f}}_{\mathrm{in},j}^k}},$$

接下来，继续在一层tpye-$k$基础上继续推导，求出$W^{\ell k}(x)$的表示。
现在，对
$f_{out,i}^{\ell }={\sum }_{j=1}^N{W}^{\ell k}(x_j-x_i)f_{in,j}^k$施加等变约束：
$$D_{\ell }(g)f_{out,i}^{\ell }=\sum _{j=1}^N{W}^{\ell k}(R_g^{-1}(x_j-x_i))D_k(g)f_{in,j}^k$$

解释：如果原点云发生了旋转，tpye-$\ell$只需要乘以一个Wigner-D矩阵：
$$f_{\ell }\mapsto D_{\ell }(g)f_{\ell }$$

$$\Rightarrow f_{out,i}^{\ell }=\sum _{j=1}^N{D}_{\ell }(g{)}^{-1}{W}^{\ell k}(R_g^{-1}(x_j-x_i))D_k(g)f_{in,j}^k$$

$$\Rightarrow W^{\ell k}(R_g^{-1}x)=D_{\ell }(g)W^{\ell k}(x)D_k(g{)}^{-1}$$

使用公式$vec(AXB)=(B^T\otimes A)vec(X)$

$$\Rightarrow vec(W^{\ell k}(R_g^{-1}x))=(D_k(g)\otimes D_{\ell }(g))vec(W^{\ell k}(x))$$

由于$$D_k⨂D_g(g)={Q^{lk}}^T\left[\underset{J=|k-l|}{\overset{k+l}{⨁}}{D}_J(g)\right]Q^{lk}$$

$$\Rightarrow vec(W^{\ell k}(R_g^{-1}x))={Q^{lk}}^T\left[\underset{J=|k-l|}{\overset{k+l}{⨁}}{D}_J(g)\right]Q^{lk}vec(W^{\ell k}(x))$$

令${\eta }^{lk}(x)\triangleq Q^{lk}vec(W^{lk}(x))$

$$\Rightarrow {\eta }^{lk}(R_g^{-1}x)=\left[\underset{J=|k-l|}{\overset{k+l}{⨁}}{D}_J(g)\right]{\eta }^{lk}(x)$$

因此${\eta }^{lk}(R_g^{-1}x)$的第$J$个向量${\eta }_J^{lk}(R_g^{-1}x)$受到约束：
$${\eta }_J^{lk}(R_g^{-1}x)=D_J(g){\eta }_J^{lk}(x)$$

这正是的球谐波的变换定律:
$$Y_J(R_g^{-1}x)=D_J^{\ast }(g)Y_J(x),x\in S^2,g\in G$$
$D_J$是第$J$个Wigner-D matrix，$D_J^{\ast }$是它的共轭

因此，$W^{lk}(x)$可以被构造为：
$$vec⟮W^{lk}(x)⟯={Q^{lk}}^T\underset{J=|k-l|}{\overset{k+l}{⨁}}{Y}_J(x)$$

4.9 再次理解Tensor Field Layers

$${\mathbf{f}}_{\mathrm{out},i}^{\ell }=\sum _{k\ge 0}\sum _{j=1}^n\underset{\text{node }j\to \text{ node }i\text{ message }}{\underbrace{{\mathbf{W}}^{\ell k}\left({\mathbf{x}}_j-{\mathbf{x}}_i\right){\mathbf{f}}_{\mathrm{in},j}^k}}$$
假设$f_{in}=f_{in}^0$，并且有：$$f_{in}^0\mapsto f_{out}^0$$ $$f_{in}^0\mapsto f_{out}^1$$
现在加上self-interaction
$${\mathbf{f}}_{\mathrm{out},i}^{\ell }=\underset{\text{self-interaction}}{\underbrace{w^{\ell \ell }{f}_{in,i}^{\ell }}}+\sum _{k\ge 0}\sum _{j=1}^n\underset{\text{node }j\to \text{ node }i\text{ message }}{\underbrace{{\mathbf{W}}^{\ell k}\left({\mathbf{x}}_j-{\mathbf{x}}_i\right){\mathbf{f}}_{\mathrm{in},j}^k}}$$

只有$k=l时才有self-interaction$