卷积神经网络(CNN)

卷积神经网络(CNN)

  本blog先介绍对卷积的理解，然后介绍卷积神经网络，同时介绍了较为简单的LeNet-5卷积神经网络。卷积神经网络的输入可以是，一维、二维甚至三维的数据，所以在图像识别等计算机视觉领域以及自然语言处理领域用的较多。

1. 卷积

1.1. 离散卷积的理解

  以离散卷积为例，对序列$x(n)$与$h(n)$，我们熟知的卷积定义如下$$y(n)=\sum _{-\infty }^{i=\infty }x(i)h(n-i)=x(n)\ast h(n)$$

  直观来看，这是两个序列进行卷积得到另一个序列，属于泛函分析范畴。具体来看，$x(n_1)$的自变量取值与$h(n_2)$的自变量取值满足某种约束，即$n_1+n_2=n$，也就是说，$x(n_1)$的自变量$n_1$与$h(n_2)$的自变量$n_2$在坐标轴上关于$\frac{n}{2}$对称，所有的$n_1$都有关于$\frac{n}{2}$对称的$n_2$，我们对$x(n_1)$与$h(n_2)$的所有乘积求和就是卷积的结果$y(n)$。
  从实际运算来看，假设$x(-1)=a,x(0)=b,x(1)=c,h(3)=i,h(4)=g,h(5)=t$，其余的值均为0，则$y(n)=\sum _{-\infty }^{i=\infty }x(i)h(n-i)=x(n)\ast h(n)$的分解运算如下图所示

根据上面的说明，$h(\alpha -n)$就是把$h(n)$做关于点$\frac{\alpha }{2}$的对称，在与$x(n)$相乘并求和得到$y(\alpha )$，选择不同的$\alpha$，$h(\alpha -n)$的翻转参考点不同，效果就像是$h(\alpha -n)$在坐标轴上平移(如上图)。这一系列步骤就是我们在求卷积时熟知的"翻转、相乘、相加、平移"。
  重点看图中的平行四边形画出的部分，这一部分才有对应的$y$值(其余$y$值为0)，我们是否也可以这样理解卷积，把序列$x(-1)、x(0)、x(1)$与$h(3)$相乘，结果分配到$y^{\prime }(2)、y^{\prime }(3)、y^{\prime }(4)$，类似的把序列$x(-1)、x(0)、x(1)$分别与$h(4)、h(5)$相乘，结果分别分配到$y^{\prime }(3)、y^{\prime }(4)、y^{\prime }(5)$与$y^{\prime }(4)、y^{\prime }(5)、y^{\prime }(6)$，$y^{\prime }$表示是$y$的中间结果，然后把分配到$y^{\prime }(2),y^{\prime }(3),y^{\prime }(4),y^{\prime }(5),y^{\prime }(6)$上的值相加，就是最终的结果。这就引出了卷积的另一个理解，即一个序列在另一个序列上的加权叠加。
  如何确定第一个非零的$y$值的位置？从上面的分析中，我们其实可以总结出来规律：$x(n)$序列的第一个非零元素对应的自变量值与$h(n)$序列的第一个非零元素对应的自变量值的和，即是卷积结果$y(n)$的第一个非零元素对应的自变量值。以上面的例子为例，$y(n)$的第一个非零元素就是$y(3+(-1))$。

1.2. 离散卷积的实际应用例子

  举一个离散卷积的应用场景，假设我们先后投一枚骰子，两次投掷结果的概率分别记为$f_1(n)$与$f_2(n)$，在$n=1,2\dots 6$时才有非零概率，其余的$n$值对应概率均为0，现在我们想求两次投掷结果之和等于4的概率，用卷积的运算很容易就可以描述这种求解$$y(4)=\sum _{-\infty }^{i=\infty }{f}_1(i)f_2(4-i)=f_1(0)f_2(3)+f_1(2)f_2(2)+f_1(3)f_2(1)$$

1.3. 卷积的矩阵用法

  如果我们的卷积对象不再是两个一维序列，而是两张图(二维矩阵图)，卷积操作依然会按照旋转，相乘，相加，平移的流程执行。假设我们有这样两个矩阵$$A=\left[\begin{array}{ccccc}{a}_{(0,0)}& a_{(0,1)}& a_{(0,2)}& a_{(0,3)}& a_{(0,4)}\\ a_{(1,0)}& a_{(1,1)}& a_{(1,2)}& a_{(1,3)}& a_{(1,4)}\\ a_{(2,0)}& a_{(2,1)}& a_{(2,2)}& a_{(2,3)}& a_{(2,4)}\\ a_{(3,0)}& a_{(3,1)}& a_{(3,2)}& a_{(3,3)}& a_{(3,4)}\\ a_{(4,0)}& a_{(4,1)}& a_{(4,2)}& a_{(4,3)}& a_{(4,4)}\end{array}\right]$$$$B=\left[\begin{array}{ccc}{b}_{(-1,-1)}& b_{(-1,-1)}& b_{(-1,-1)}\\ b_{(0,0)}& b_{(0,0)}& b_{(0,0)}\\ b_{(1,1)}& b_{(1,1)}& b_{(1,1)}\end{array}\right]$$

注意B矩阵的下标从-1开始，而A矩阵的下标从0开始，这样是为了保证，B矩阵在A矩阵上投影的中心位置，和卷积结果的中心位置一致(都是(m,n))。则矩阵的卷积定义如下：$$Y(m,n)=A\ast B=\sum _x\sum _{y}A(x,y)\times B(m-x,n-y)$$

这样A，B矩阵的对应元素位置，就关于$(\frac{m}{2},\frac{n}{2})$对称，和一维序列的卷积类似。当$m,n$递增，就会出现B矩阵在A矩阵上滑动的效果，如下图，这里$B$矩阵已经经过翻转， m , n = { 1 , 2 , 3 } m,n=\{1,2,3\} m,n={ 1,2,3}：

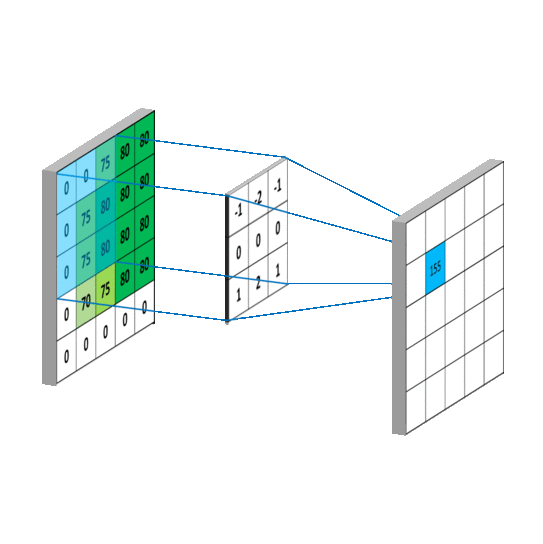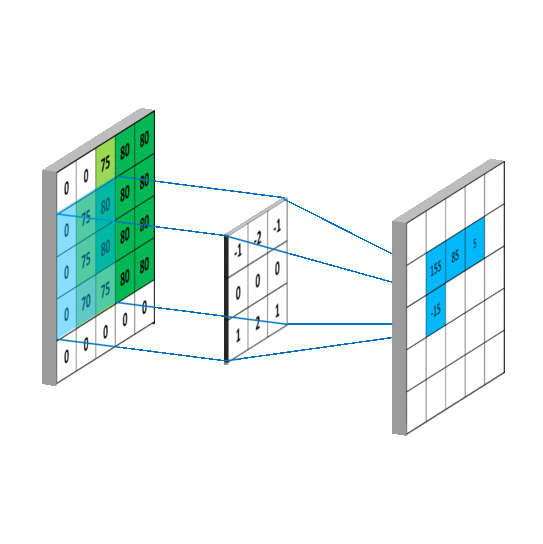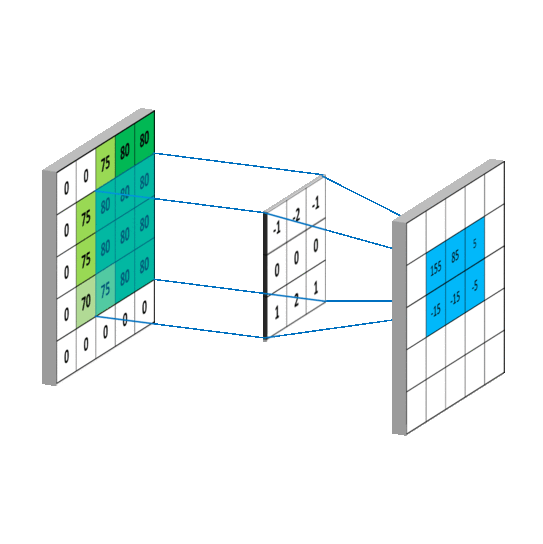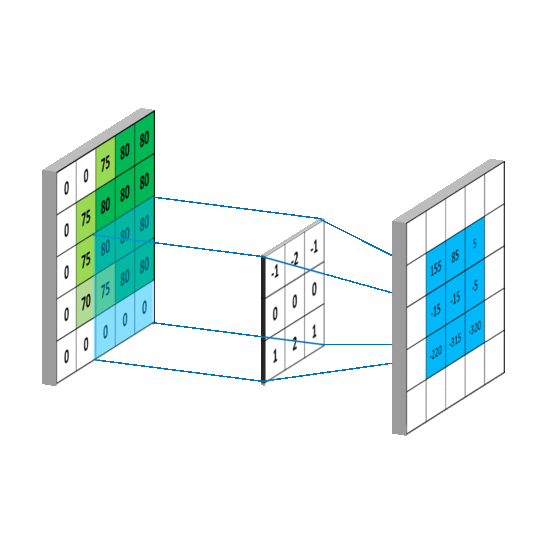
  同时，考虑A矩阵的边界，当$m=0$或$n=0$时，$B$矩阵以$(\frac{m}{2},\frac{n}{2})$为中心翻转后，有一部分值对应在$A$矩阵中的位置，没有对应的数据，为了解决这一问题，我们在A矩阵外围，填充(padding)一圈数据，如下图

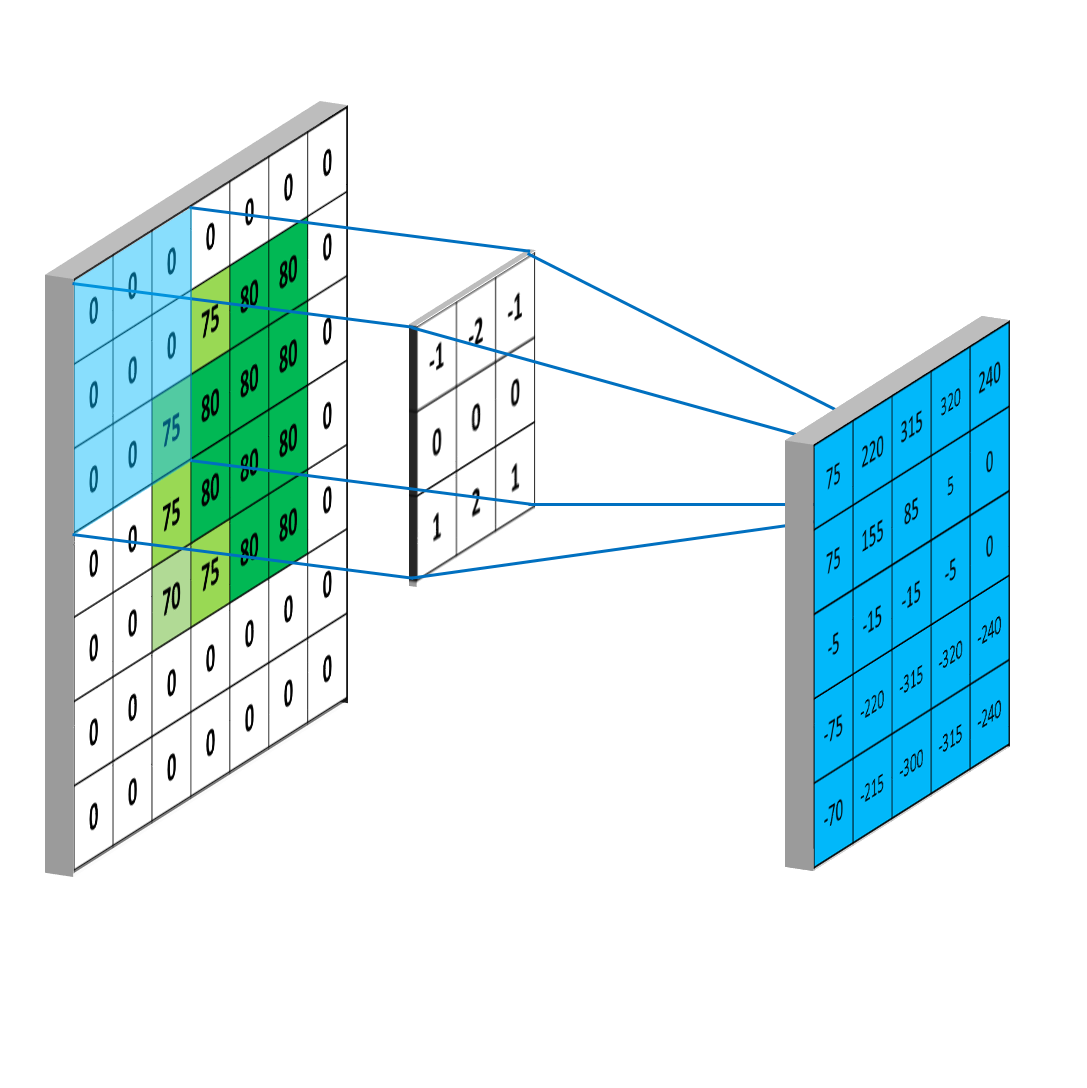
这样，$A$矩阵就有了位置下标是-1的数据，同时，我们卷积得到的矩阵结果，就和A矩阵大小一样。原则上，可以在A矩阵外填充两层0，但是这样得到的矩阵结果就大于A矩阵，所以一般不这么做；如果在A矩阵外填充更多层的0，这些位置的卷积结果都是0，更没有意义去考虑。

  矩阵卷积是CNN的基础，同时也用在图像平滑处理等多个领域。

  由于我们可以把矩阵B在存储时就存成翻转后的格式，所以在实际卷积时，只用考虑"相乘、相加、平移"，不用进行翻转操作，后面blog中的$"\ast "$默认也是不发生翻转的卷积。

1.4. 矩阵的卷积转化成矩阵运算

  这里的卷积操作不考虑翻转过程，也就是说，存储时就存成了翻转后的形式。定义$A,B$矩阵如下 A = [ a ( 0 , 0 ) a ( 0 , 1 ) a ( 0 , 2 ) a ( 0 ,