Andrew NG 《machine learning》week 6,class2—Bias vs. Variance

Andrew NG 《machine learning》week 6,class2—Bias vs. Variance

当你运行一个机器学习算法的时候，大多数运行不理想的情况要么是偏差比较大，要么是方差比较大。即出现的情况要么是过拟合，要么是欠拟合，那么这两者和方差以及偏差是一一对应呢还是两者都有关系呢？能判断这个算法是偏差还是方差的问题，那么就可以有针对性的解决问题了。

2.1　Diagnosing Bias vs. Variance

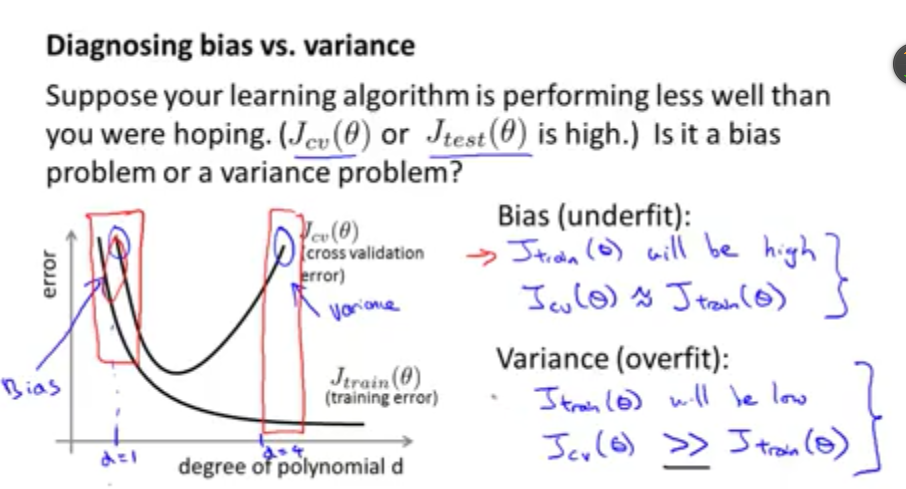
对于欠拟合和过拟合分别对应着高方差还是高偏差。下图给出了很好的解释。

如上图所示，分别画出了不同的假设函数对应的训练数据集的误差以及交叉验证数据集所对应的误差曲线。从图中可以看出在欠拟合和过拟合情况下，训练数据集的误差和交叉验证数据集的误差之间的关系。

2.1 Regularization and Bias/Variance

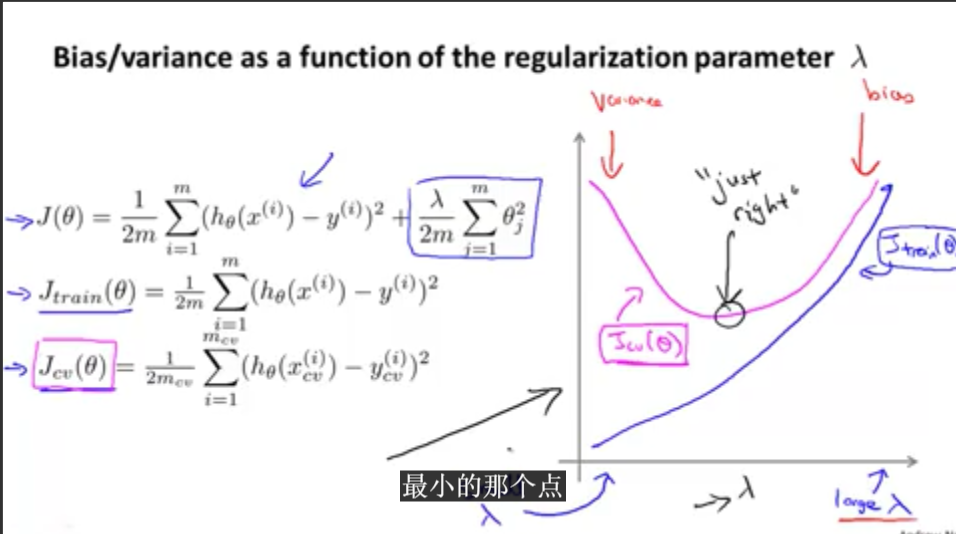
之前说过，对于解决算法的过拟合或者欠拟合，可以采用正则化的方法。本小节将会讨论正则化与偏差和方差的关系。

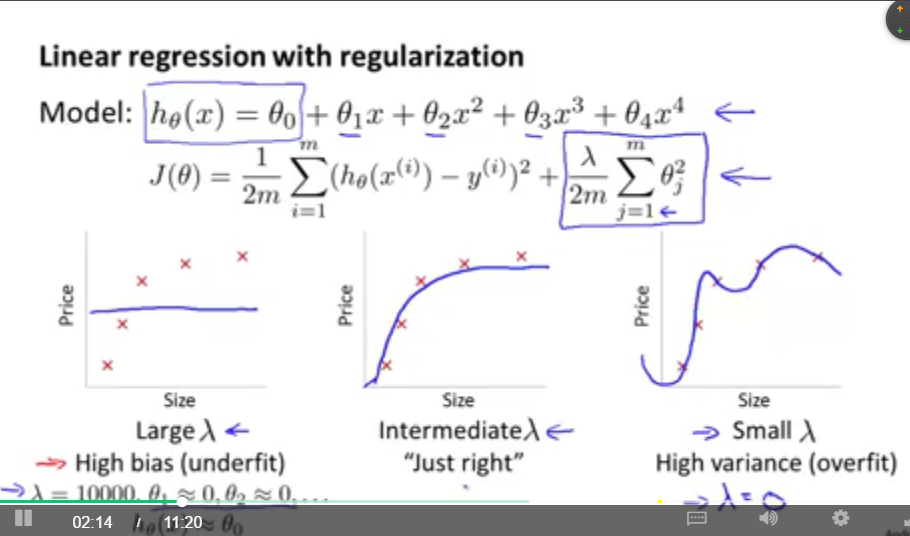
如图所示，当正则化参数lambda很大的时候，参数 thera基本都为零，这个时候就是欠拟合状态，就会出现高偏差的情况，当lambda很小的时候，就会出现过拟合情况，就是高方差的情况。

1.3 Learning Curves

本小节将会讨论绘制学习曲线的问题。学习曲线可以用来检测算法是否运行正常或者改进的算法是否已经匹配。经常会用学习曲线判断一个算法是否处于偏差、方差或者两者之间的情况。
下图表示一般情况下训练误差和验证误差的曲线:

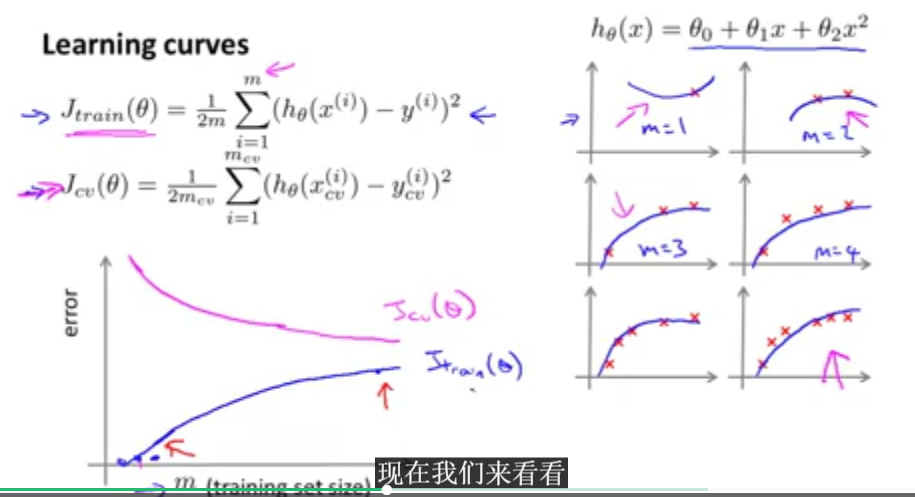
下图表示的是高偏差（欠拟合）情况下的误差曲线：

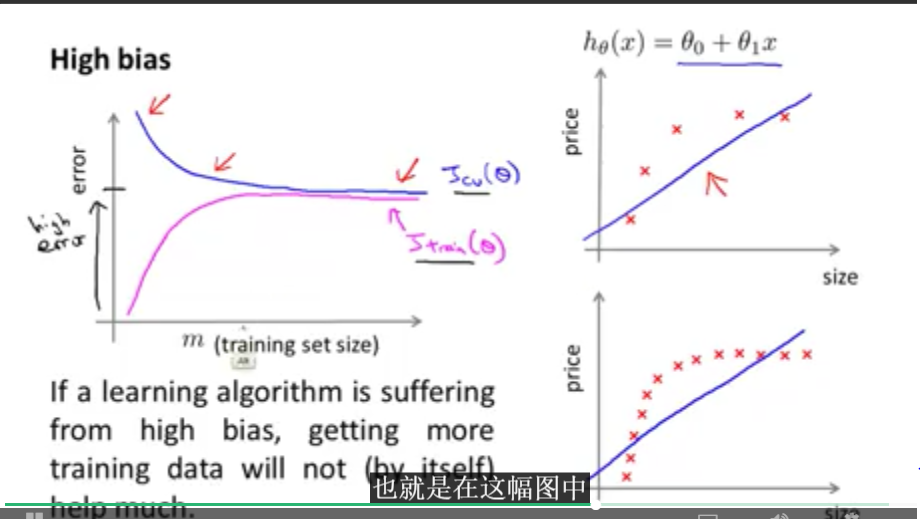
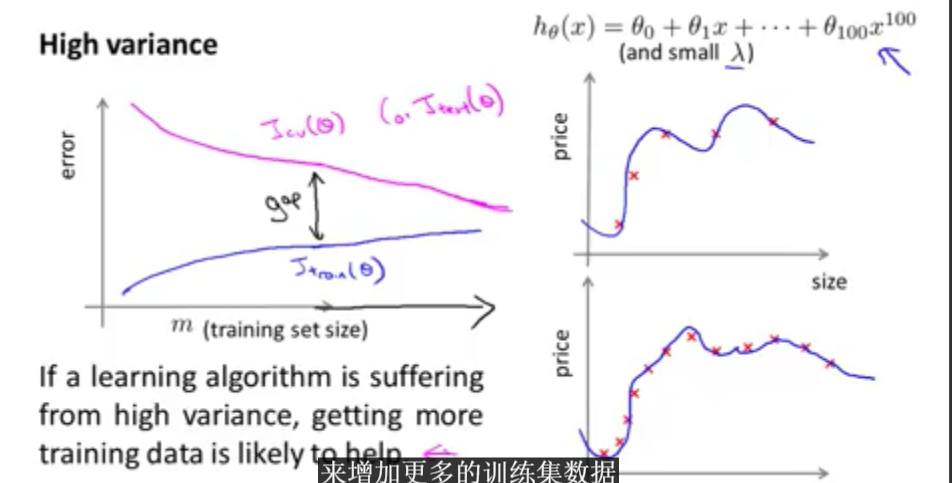
下图表示的是高方差（过拟合）情况下的误差曲线：

2.4 Deciding What to Do Next Revisited

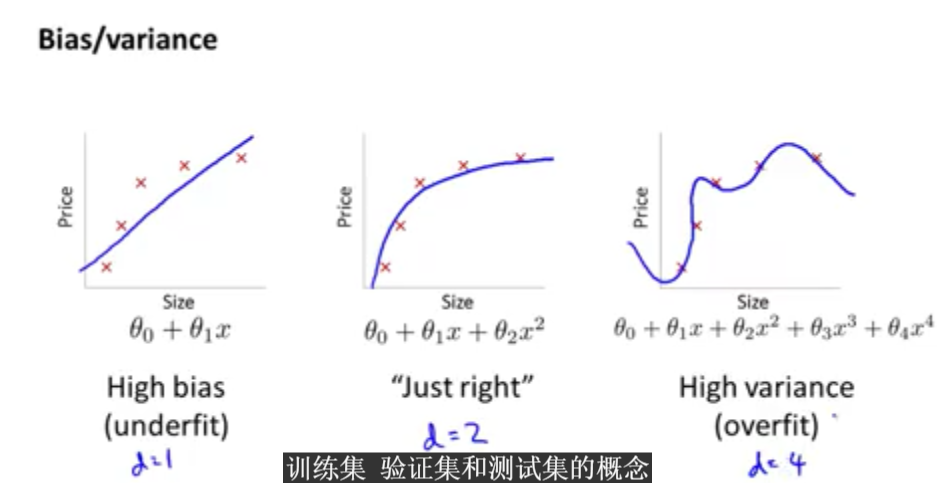
回到最初的问题，对于改进算法的方法的选择，现在可以有一个明确的划分了。如下图：

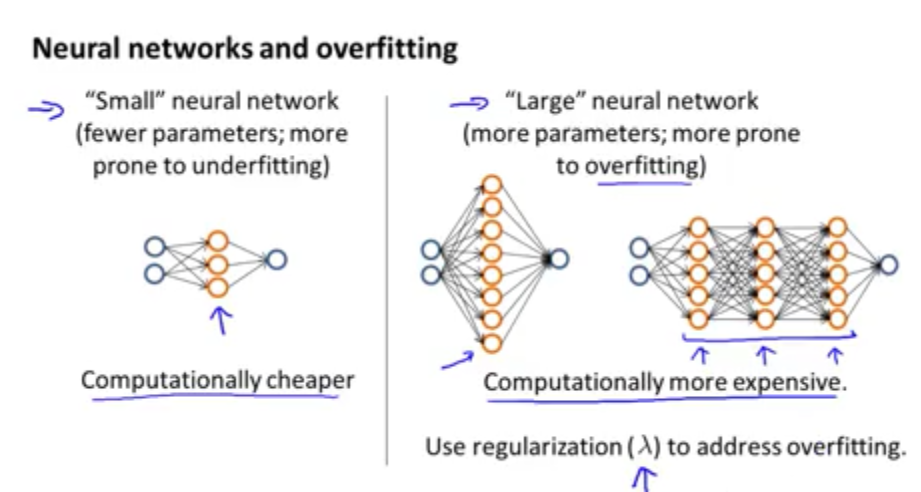
关于神经网络算法的实例如下图：