【代码随想录笔记】回溯算法总结（组合、切割、子集、排列、棋盘）

沧海既平

已于 2024-06-06 21:29:01 修改

阅读量670

点赞数 23

文章标签：笔记算法 leetcode c++

于 2024-06-06 21:12:34 首次发布

本文链接：https://blog.csdn.net/Lindy_pass/article/details/139464475

版权

参考资料：代码随想录-回溯算法

0 回溯算法理论基础

回溯法是一种用递归+剪枝模拟穷举的方法。
一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的组合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

回溯法解决的问题都可以抽象为树形结构，这类问题的解题模板为：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

在写回溯题目时，我们需要思考三个地方：递归函数的返回值以及参数、回溯函数终止条件和单层搜索的过程

1 组合问题

N个数里面按一定规则找出k个数的组合

特点

需要startIndex来记录下一层递归搜索的起始位置，避免取到重复的组合
在叶子结点收集结果，当path.size() == k时，路径终止、收集结果

剪枝

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。
因此，可以修改递归中for循环的终止条件，实现剪枝。
从for (int i = startIndex; i <= n; i++) 优化为 for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)
- 已经选择的元素个数：path.size();
- 还需要的元素个数为：k - path.size();
- 列表的元素个数：n
- 列表中i之后（包括i）的元素个数（n-i+1） >= 还需要的元素个数（k - path.size()）
  ==> i <= n - (k - path.size()) + 1

去重

所谓去重，面对的是集合内有重复元素，允许组合内有重复元素、但不允许有重复的组合的情况。
比如，给定集合[1,1,1,2,2]，要求找出所有和为3的组合。如果不进行去重处理，最后的结果会包括6个[1,2]和1个[1,1,1]，而正确的结果应该为1个[1,2]和1个[1,1,1]。
虽然可以在求出所有组合后再进行去重，但这容易导致超时，因此接下来将介绍在搜索过程中去重的方法。

出现重复的原因是，一个结点有多个重复的子结点，实际上只需要保留一个
如集合[1,1,1,2,2]，根结点的子结点中就有3个1，导致了重复。
不可以直接对集合去重，这会导致组合内也没有重复元素
直接对集合去重再进行搜索是不可行的。如集合[1,1,1,2,2]，去重得到[1,2]，最后的结果将丢失[1,1,1]
正确的去重方法为：
- 对集合排序，这能便于判断重复元素
  sort(candidates.begin(), candidates.end());
- 在每轮递归的for循环中，遇到重复元素就跳过
  if(i>startIndex && candidates[i] == candidates[i - 1]) continue;

题目

77.组合
组合问题模板题，修改for循环的终止条件实现剪枝
216.组合总和III
相比上一题加入了元素和的限制，因此在修改for循环的终止条件剪枝的基础上，根据总和再次剪枝
17.电话号码的字母组合
不同于上面两题是求同一集合内的组合，该题求不同集合之间的组合。组合中的每个字符来自于不同的集合，因此不存在重复问题，因此不需要startIndex。
39.组合总和
可以重复选取当前元素，因此递归时不用把startIndex+1
40.组合总和II
组合去重模板题，一个结点若有多个重复的子结点，只需要保留其中一个

2 切割问题

一个字符串按一定规则有几种切割方式

特点

切割问题类似于组合问题，只不过组合问题的集合为数组或字符，切割问题的集合为切割点
比如对于字符串abcd进行切割，切割问题的集合为三个切割点a/b/c/d。通过这三个切割点的选与不选，可以获得多种切割方式，如{a,bcd}、{a,b,cd}……
因此，for循环中的i仍然代表下一个从集合中被选取的元素，也即代表了下一个切割点
需要startIndex来记录下一层递归搜索的起始位置，避免取到重复的组合
在叶子结点收集结果，当startIndex == s.size()时，路径终止、收集结果

题目

131.分割回文串
切割问题模板题，以子串是否回文作为剪枝条件。
判断是否回文有两种方法：1.双指针法，对每个字符串即时地判断是否回文；2.运用动态规划思想，提前判断好所有子串的回文性，递归时查询即可
93.复原IP地址
只能切割三次，因此需要使用pointNum记录当前的切割次数。当切割次数达到三次时路径终止，此时若第四段也合法，就收集结果。在函数体中，以子串是否合法进行剪枝 + for循环中i的终止条件剪枝。所谓for循环中i的终止条件剪枝，即因为两个切割点之间的距离不能大于3，所以i<min(startIndex+3,s.size())

3 子集问题

一个N个数的集合里有多少符合条件的子集

特点

需要startIndex来记录下一层递归搜索的起始位置，避免取到重复的组合
在树的所有结点处收集结果，当startIndex == nums.size()时，路径终止
在backtracking第一行收集结果result.push_back(path);，以防漏掉自己
路径终止时只需要单纯return，由于此时也不会进入for循环，所以其实不需要写路径终止条件

去重

参考组合问题的去重。
子集问题的去重，面对的是集合内有重复元素，允许子集内有重复元素、但不允许有重复的子集的情况。
比如，给定集合[1,2,2]，要求找出所有不重复的子集。如果不进行去重处理，最后的结果显然有2^3=8个，而正确的结果应该为[[],[1],[1,2],[1,2,2],[2],[2,2]]共6个，去掉了各一个重复的[1,2]和[2]。

出现重复的原因是，一个结点有多个重复的子结点，实际上只需要保留一个
与组合问题的去重相同，子集问题的去重也不能直接对集合去重。
正确的去重方法为：
- 对集合排序，这能便于判断重复元素
  sort(nums.begin(),nums.end());
- 在每轮递归的for循环中，遇到重复元素就跳过
  if(i>startIndex && nums[i] == nums[i-1]) continue;

题目

78.子集
子集问题模板题，在每个结点处收集答案
90.子集II
子集去重模板题，一个结点若有多个重复的子结点，只需要保留其中一个
491.非递减序列
由于这题集合中元素顺序影响结果，不能对集合排序。因此我们可以借助哈希表进行去重，对于多个重复的子结点，只保留第一个即可。由于nums[i]的取值范围不大，哈希表也可以用数组替代，能提高程序效率。另外，题中要求子集的下一个元素必须大于等于上一个，因此需要在递归时记录上一个数，通过比较大小进行剪枝。题中要求子集至少包含两个元素，因此在path.size()>=2时收集答案

4 排列问题

N个数按一定规则全排列，有几种排列方式

特点

排列是有序的，如[1,2]和[2,1]是不同的排列，因此每层都应该从0开始搜索，而不是从startIndex开始
虽然从0开始搜索，但是该条路径上已经选择过的数不能再选，因此需要used数组记录path里哪些元素已被使用
在叶子结点收集结果，当path.size() == nums.size()，路径终止、收集结果

去重

同样，去重问题面对的是集合内有重复元素，允许排列内有重复元素、但不允许有重复的排列的情况。

出现重复的原因仍然是，一个结点有多个重复的子结点，实际上只需要保留一个
不可以直接对集合去重，这会导致排列内也没有重复元素
正确的去重方法为：
- 对集合排序，这能便于判断重复元素
  sort(nums.begin(), nums.end());
- 在每轮递归的for循环中，在未被使用的元素中遇到重复的就跳过
  if(i>0 && nums[i] == nums[i-1] && used[i-1] == 0) continue; 其中used = 0代表未使用过该元素
  注意这里的used[i-1] == 0，它保证了是在未使用的元素中进行去重。设想集合nums = [1,1,2]，对于第一层的第一个结点nums[0] = 1，其子结点为nums[1] = 1和nums[2] = 2。如果不加used[i-1] == 0这句判断，nums[1] = 1也会被剔除掉。

题目

46.全排列
排列问题模板题，每层从0开始搜索，使用used数组记录path上的元素使用情况
47.全排列II
排列问题去重模板题，一个结点若有多个重复的子结点，只需要保留其中一个

5 棋盘问题

以hard题为主，集合从一维数组变成二维矩阵。回溯方法因题而异，接下来按题进行分析。

N皇后

51.N皇后
题目：将 n 个皇后放置在 n×n 的棋盘上，任意两个皇后不能处于同一行或同一列或同一斜线上。
分析题目可知，每行有且仅有1个皇后。因此，可以将棋盘的每一行看作树的每一层，问题变为从n个长为n的集合中各选1个数，选出的组合满足N皇后的定义。比较类似于组合问题中的17.电话号码的字母组合。在判断当前选择的皇后是否合法的时候，要判断同列、45°斜线、135°斜线上是否已经存在皇后。
在这里插入图片描述

相关题目
- 52.N皇后II

解数独

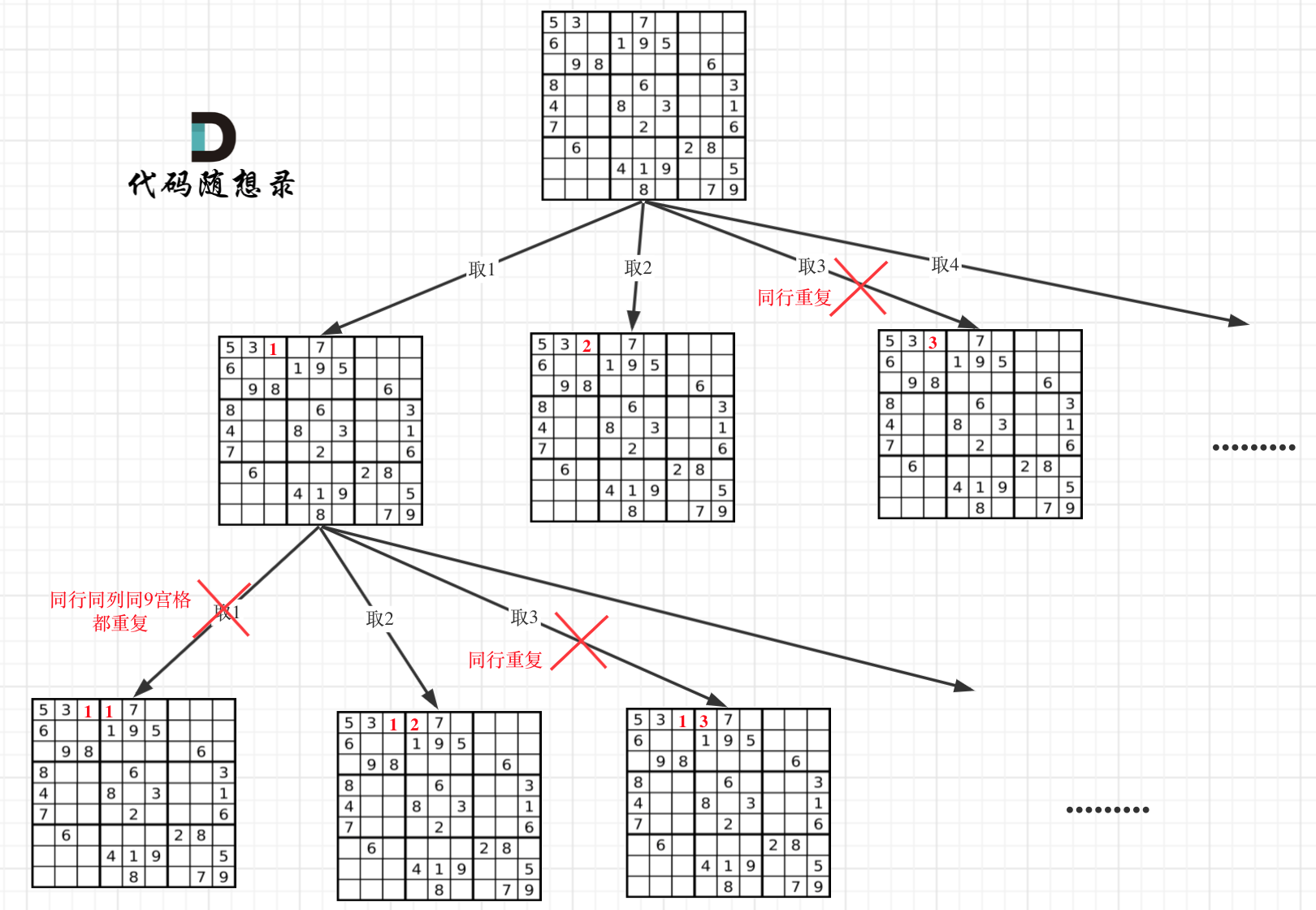
37.解数独
枚举每个空白格上的可能，如果该可能满足数独性质（同行、同列、九宫格内无重复），就递归搜索，否则回溯。由于题目保证每个输入有且仅有唯一解，因此当找到一个解后应立刻返回，终止backtracking。因此，可以将backtracking的返回值设置为bool，将常规的递归语句改为if (backtracking(board)) return true;即可。在填数字时，由于之前的数字填错，当前空格是有可能出现填什么都不对的情况的：比如第一行填成[5,3,2,6,7,4,8,9,.]此时前八个数符合数独要求，但是第九个格子填什么都不对，这是因为之前填错了，需要终止这种路径。
在这里插入图片描述