前言
最近在一个项目中接触到了卡尔曼滤波,并且对此进行了学习,发现其是一个很有意思的信息融合的算法,可以结合多种传感器的信息(存在噪声),得到更为理想的估计,因此在此进行笔记和心得纪录。本人不是从事控制相关专业工作,可能在短暂的自学过程中对此存在误解,若有谬误,望联系指出,谢谢。(文章主要参考了[1])
∇ \nabla ∇ 联系方式:
e-mail: FesianXu@gmail.com
QQ: 973926198
github: https://github.com/FesianXu
知乎专栏: 计算机视觉/计算机图形理论与应用
微信公众号:

从传感器的测量谈起
在正式讨论卡尔曼滤波前,我们先讨论对物理量的测量。我们会发现是和卡尔曼滤波紧密相关的。
我们知道,如果需要对自然界的某个物理量,比如温度,气压,速度等进行测量,我们需要用各种传感器进行测量。但是,因为器件的工艺不可能达到完美,或者其他不能被人为预测到或者控制到的因素和噪声等存在,传感器对物理量的预测不可能是完全准确的。因此,我们与其把传感器的测量结果当成是一个确定值,不如把它看成是一个随机变量
v
v
v,其均值和方差分别为
μ
,
σ
2
\mu, \sigma^2
μ,σ2,既是
v
∼
P
(
μ
,
σ
2
)
v \sim P(\mu, \sigma^2)
v∼P(μ,σ2),这两个统计参数描述了测量的输出值(也就是我们直接观察到的值)和对这个测量的可信程度。同时,我们要注意到,这里的
μ
,
σ
2
\mu, \sigma^2
μ,σ2不一定是时间平稳的,也就是说可能随着时间的变化而变化。 (暂且假设传感器的测量均值是和真实值无偏的。)
如下图所示,如果直接观察传感器数据,那么其可能是会存在很大的抖动,而不是平滑的,原因可能是观察噪声的影响。

我们这个时候就想到,如果一次观察是抖动的,有着 σ 2 \sigma^2 σ2的不确定的,那么如果用同一个传感器对这个物理量观察 N N N次,然后对 N N N次数据进行求和,以减少不确定性的影响,岂不妙哉? 这样的确是可以的,这个就是信号处理当中的滑动窗口均值滤波(mean filter)。但这个简单操作有几个缺点:
- 我们前面谈到了不确定度 σ 2 \sigma^2 σ2是可能时变的,简单相加不能最好地消除不确定性。
- 时间上滑动窗口进行多次测量的求和,会导致延迟。
对此,我们进行一个小改进,就是用多个相同的传感器去同时测量一个物理量,然后求和或者根据可靠程度去求加权平均和,我们假设多个传感器的采样值
x
i
x_i
xi满足分布,其中
i
i
i表示传感器序号:
x
i
∼
P
(
μ
,
σ
i
2
)
(1.1)
x_i \sim P(\mu, \sigma_i^2) \tag{1.1}
xi∼P(μ,σi2)(1.1)
我们发现,其因为假设是无偏测量传感器因此均值相同,但是每个传感器的不确定性不一定相同。
这个时候简单的求和就容易造成结果的偏移,我们不妨根据方差的大小,进行加权平均求和,在此之前,我们需要几个假设:
- 不同传感器的测量都是一个随机变量,其均值 μ \mu μ相同。
- 不同传感器的测量之间是无关的,也就是说知道了 x i x_i xi不能对知道其他策略 x j x_j xj提供任何信息,但是也不会影响到观测 x j x_j xj的均值,即是 E ( x j ∣ x i ) = E ( x j ) E(x_j|x_i) = E(x_j) E(xj∣xi)=E(xj)。
接下来,我们用这两个假设,进行简单的传感器间的数据融合以提高测量效果。Let’s move on!
简单版本,多传感器数据融合
为了简单起见,假设我们用两个相同的传感器进行测量,那么最后数据融合结果应该是:
x
^
=
α
x
1
+
β
x
2
α
+
β
=
1
⇒
x
^
=
α
x
1
+
(
1
−
α
)
x
2
(2.1)
\begin{aligned} &\hat{x} = \alpha x_1 + \beta x_2 \\ &\alpha+\beta=1 \\ \Rightarrow \hat{x} &= \alpha x_1 + (1-\alpha) x_2 \end{aligned} \tag{2.1}
⇒x^x^=αx1+βx2α+β=1=αx1+(1−α)x2(2.1)
那么,融合后的估计
x
^
\hat{x}
x^的不确定度可以通过
x
1
,
x
2
x_1, x_2
x1,x2的方差进行衡量,公式如:
σ
^
2
(
α
)
=
(
1
−
α
)
2
σ
1
2
+
α
σ
2
2
(2.2)
\hat{\sigma}^2 (\alpha) = (1-\alpha)^2 \sigma_1^2 + \alpha \sigma_2^2 \tag{2.2}
σ^2(α)=(1−α)2σ12+ασ22(2.2)
为了最小化
σ
^
2
(
α
)
\hat{\sigma}^2(\alpha)
σ^2(α),我们用求导并且置为0的方法[3],不难推导出当
α
=
σ
1
2
σ
1
2
+
σ
2
2
\alpha = \dfrac{\sigma_1 ^2}{\sigma_1^2+\sigma_2^2}
α=σ12+σ22σ12时,式子(2.2)有最小值,此时,式子(2.1)可化为:
x
^
(
x
1
,
x
2
)
=
σ
2
2
σ
1
2
+
σ
2
2
x
1
+
σ
1
2
σ
1
2
+
σ
2
2
x
2
(2.3)
\begin{aligned} \hat{x}(x_1, x_2) &= \dfrac{\sigma_2^2}{\sigma_1^2+\sigma_2^2} x_1 + \dfrac{\sigma_1^2}{\sigma_1^2+\sigma_2^2} x_2 \end{aligned} \tag{2.3}
x^(x1,x2)=σ12+σ22σ22x1+σ12+σ22σ12x2(2.3)
这里讨论的只是两个传感器的情况,可以简单地推导到多个传感器的情况和当观测值是一个向量时候的情况,以及为了计算有效性,采用迭代计算的方法,具体可以参考文献[3]。其中,为了以后讨论的方便,这里给出当观测值是一个向量,并且只有两个传感器时的公式(2.4):
x
1
∼
p
1
(
μ
1
,
Σ
1
)
,
x
2
∼
p
2
(
μ
2
,
Σ
2
)
K
=
Σ
1
Σ
1
+
Σ
2
x
^
=
x
1
+
K
(
x
2
−
x
1
)
Σ
y
y
=
(
I
−
K
)
Σ
1
(2.4)
\begin{aligned} & \mathbf{x}_1 \sim p_1(\mathcal{\mu}_1, \Sigma_1), \mathbf{x}_2 \sim p_2(\mathbf{\mu}_2, \Sigma_2) \\ & K = \dfrac{\Sigma_1}{\Sigma_1+\Sigma_2} \\ & \hat{x} = \mathbf{x}_1 + K(\mathbf{x}_2 - \mathbf{x}_1) \\ & \Sigma_{\mathbf{yy}} = (I-K) \Sigma_1 \end{aligned} \tag{2.4}
x1∼p1(μ1,Σ1),x2∼p2(μ2,Σ2)K=Σ1+Σ2Σ1x^=x1+K(x2−x1)Σyy=(I−K)Σ1(2.4)
可以发现,此时不再假设每个传感器的测量均值都是一样的了,其中的
K
K
K称之为卡尔曼增益(Kalman Gain),嘛,这里不过只是个名字,暂且不管。
卡尔曼滤波,开始征程
接下来我们开始正式讨论卡尔曼滤波(Kalman Filter)。我们之前讨论的传感器之间其实都是**无关(uncorrelated)**的,但是,其实经常我们知道了某个测量量,是可以确定或者为确定另一个测量量提供信息量的,比如我们现在需要测量车辆的位置和速度,那么知道了速度,通常可以为下一步知道位置提供一定的信息。在这种前提下,我们便能够通过更为合理的数据融合手段,得到更为精确的估计结果。
定位问题[1]
考虑一个例子,我们的机器人需要定位,通常使用的是GPS进行定位,得到车辆的状态量之一的位置:
p
p
p 。其次,我们可以通过测量轮子的转过的圈数,对机器人的运行速度进行测量,得到状态量另一个,速度:
v
v
v。但是,我们要牢记,我们的观测不是完全准确的,比如GPS存在误差,而测量轮子转过的圈数也不能完美的描述速度,因为可能因为地面不平,轮胎打滑等原因导致误差。不过我们记住我们这个例子中的两个状态量:
x
⃗
k
=
{
p
⃗
,
v
⃗
}
\vec{x}_k = \{\vec{p}, \vec{v}\}
xk={p,v}
在这个情况下,我们对两个状态量的观测其实是一个两元的概率变量,我们的每个观测都落在分布之中,而我们的任务就是从这个不确定性高的分布中,得到个不确定性更小的分布,从而得到更为精确的估计。图如:


这个时候,观测的不确定性体现在方差 σ 2 \sigma^2 σ2上,而观测值可以用均值向量 μ \mathbf\mu μ描述,如Fig 4所示:

状态预测方程
这个时候,如果我们的观测是准确的,那么会出现什么情况呢?我们根据牛顿力学,可以对位置-速度的过程进行建模,我们会有:
p
⃗
k
=
p
⃗
k
−
1
+
Δ
t
⋅
v
⃗
v
⃗
k
=
v
⃗
k
−
1
(3.1)
\begin{aligned} \vec{p}_k &= \vec{p}_{k-1} + \Delta t \cdot \vec{v} \\ \vec{v}_k &= \vec{v}_{k-1} \end{aligned} \tag{3.1}
pkvk=pk−1+Δt⋅v=vk−1(3.1)
用矩阵形式表达就是:
x
^
k
=
[
1
Δ
t
0
1
]
x
^
k
−
1
=
F
k
x
^
k
−
1
(3.2)
\begin{aligned} \mathbf{\hat{x}}_k &= \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} \mathbf{\hat{x}}_{k-1} \\ &= \mathbf{F}_k {\mathbf{\hat{x}}_{k-1}} \end{aligned} \tag{3.2}
x^k=[10Δt1]x^k−1=Fkx^k−1(3.2)
其中,
x
^
k
\mathbf{\hat{x}}_{k}
x^k表示的是状态向量,为
x
^
k
=
[
p
⃗
,
v
⃗
]
T
\mathbf{\hat{x}}_k = [\vec{p}, \vec{v}]^T
x^k=[p,v]T。
我们称 F k = [ 1 Δ t 0 1 ] \mathbf{F}_k = \begin{bmatrix} 1 & \Delta t \\ 0 & 1 \end{bmatrix} Fk=[10Δt1]为预测矩阵(Predict Matrix),通过此,我们可以用当前时刻 k − 1 k-1 k−1的状态量去预测下一个时刻 k k k的状态量,即使我们并不知道真实的值应该是多少,但是这并不影响我们对状态的预测。
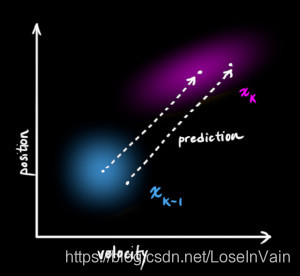
当在用 F k \mathbf{F}_k Fk进行描述这个预测时,其实可以看成是点对之间的线性变换,那么如Fig 6所示:
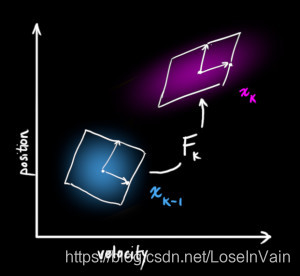
那么此时,预测的状态量
x
^
k
\mathbf{\hat{x}}_{k}
x^k有了,还需要预测
k
k
k时刻的不确定性,也就是方差,在多变量情况下是协方差矩阵,用
P
k
\mathbf{P}_{k}
Pk表示:
P
k
=
F
k
P
k
−
1
F
k
T
(3.3)
\mathbf{P}_k = \mathbf{F}_k \mathbf{P}_{k-1} \mathbf{F}_k^T \tag{3.3}
Pk=FkPk−1FkT(3.3)
于是我们有,状态量预测和协方差预测:
x
^
k
=
F
k
x
^
k
−
1
P
k
=
F
k
P
k
−
1
F
k
T
(3.4)
\begin{aligned} \mathbf{\hat{x}}_k &= \mathbf{F}_k {\mathbf{\hat{x}}_{k-1}} \\ \mathbf{P}_k &= \mathbf{F}_k \mathbf{P}_{k-1} \mathbf{F}_k^T \end{aligned} \tag{3.4}
x^kPk=Fkx^k−1=FkPk−1FkT(3.4)
考虑施加外力的情况,添加控制项
在控制理论问题中,我们怎么能忘记添加控制项呢?毕竟我们都希望整个系统是可控制的,而不是任其随意发展的。
让我们继续扩展我们上面的那个例子。考虑到机器人本身有油门,可以进行一定的加速行驶,也可以按照一定的加速度制动,让我们假设这个加速度为
a
a
a,那么根据牛顿力学,我们的状态预测方程(3.1)就更新为:
p
k
=
p
k
−
1
+
1
2
a
Δ
t
2
v
k
=
v
k
−
1
+
a
Δ
t
(3.5)
\begin{aligned} p_k &= p_{k-1} + \frac{1}{2} a \Delta t^2 \\ v_k &= v_{k-1}+a \Delta t \end{aligned} \tag{3.5}
pkvk=pk−1+21aΔt2=vk−1+aΔt(3.5)
同样还是用矩阵形式表达,有:
x
^
k
=
F
k
x
^
k
−
1
+
[
Δ
t
2
2
Δ
t
]
a
=
F
k
x
^
k
−
1
+
B
k
u
k
(3.6)
\begin{aligned} \mathbf{\hat{x}}_k &= \mathbf{F}_k \mathbf{\hat{x}}_{k-1}+\begin{bmatrix} \frac{\Delta t^2}{2} \\ \Delta t \end{bmatrix} a \\ &= \mathbf{F}_k \mathbf{\hat{x}}_{k-1}+\mathbf{B}_k \mathbf{u}_k \end{aligned} \tag{3.6}
x^k=Fkx^k−1+[2Δt2Δt]a=Fkx^k−1+Bkuk(3.6)
其中,
B
k
\mathbf{B}_k
Bk被称之为控制矩阵(Control Matrix),
u
k
\mathbf{u}_k
uk被称之为控制向量(Control Vector) 。如果一个系统实在是没有控制项,那么可以忽视这个控制项。
然而,因为一系列的误差存在,我们的预测不可能是完全准确的。那么我们的误差或者是不确定性主要在哪里存在呢?
导致预测或者观察不确定性的因素
有以下四种因素可能导致我们的状态预测或者观察存在不确定性[2],我们对此进行简单描述:
- 参数的不确定性:参数不确定性指的是在对预测进行建模时,比如 F = M a F=Ma F=Ma,这个模型通过参数 M M M进行建模,然而对这个参数的观察不可能是百分百精确的,这个参数的误差就会导致整个模型的误差,因此状态预测这个时候更新为:
x ^ k = ( F k + Δ F k ) x ^ k − 1 + ( B k + Δ B k ) u k (s1) \mathbf{\hat{x}}_{k} = (\mathbf{F}_k+\Delta \mathbf{F}_k)\mathbf{\hat{x}}_{k-1} + (\mathbf{B}_k+\Delta \mathbf{B}_k) \mathbf{u}_k \tag{s1} x^k=(Fk+ΔFk)x^k−1+(Bk+ΔBk)uk(s1)
- 控制器的不确定性:实际生活中,我们的控制器同样不可能完美,这个误差可以建模为:
x ^ k = F k x ^ k − 1 + ( B k + Δ B k ) u k (s2) \mathbf{\hat{x}}_{k} = \mathbf{F}_k\mathbf{\hat{x}}_{k-1} + (\mathbf{B}_k+\Delta \mathbf{B}_k) \mathbf{u}_k \tag{s2} x^k=Fkx^k−1+(Bk+ΔBk)uk(s2)
- 模型的不确定性:实际中,我们通过简单的线性建模不一定能很好地表达模型预测,因此要引入一个残差项,表示模型的不完美,建模为:
x ^ k = F k x ^ k − 1 + B k u k + f ( x ^ k − 1 , u k ) (s3) \mathbf{\hat{x}}_{k} = \mathbf{F}_k\mathbf{\hat{x}}_{k-1} + \mathbf{B}_k \mathbf{u}_k + f(\mathbf{\hat{x}}_{k-1}, \mathbf{u}_k) \tag{s3} x^k=Fkx^k−1+Bkuk+f(x^k−1,uk)(s3)
- 观测不确定性:就像我们之前谈到的,我们的观测也是不完美的。
描述不确定性
正如上一节我们谈到的,有一些影响状态的因素,比如风,地面情况,轮胎打滑或者其他各种小情况我们是没法完全考虑到的,也就没法建模出来,这个时候,状态预测结果就存在不确定性,如Fig 7所示:

我们为了对未能跟踪到的变量进行统一建模,我们假设状态从 x ^ k − 1 \mathbf{\hat{x}}_{k-1} x^k−1到下一个时刻状态,其下一个状态落在一个协方差为 Q k \mathbf{Q}_k Qk的高斯分布中,也就是说,我们把所有未能跟踪到的影响因素都用这个高斯分布描述了。
这个影响导致了我们式子(3.4)中的协方差发生了变化,但是其均值不变,公式如:
x
^
k
=
F
k
x
^
k
−
1
+
B
k
u
k
P
k
=
F
k
P
k
F
k
T
+
Q
k
(3.7)
\begin{aligned} \mathbf{\hat{x}}_k &= \mathbf{F}_k \mathbf{\hat{x}}_{k-1} + \mathbf{B}_k \mathbf{u}_k \\ \mathbf{P}_k &= \mathbf{F}_k \mathbf{P}_k \mathbf{F}_k^T + \mathbf{Q}_k \end{aligned} \tag{3.7}
x^kPk=Fkx^k−1+Bkuk=FkPkFkT+Qk(3.7)
以上的内容只是对预测结果进行了讨论,但是实际上我们除了预测,还会存在传感器的测量,虽然这个测量是不准确的,但是也能提供一定的信息量。
根据观测结果对估计进行调整
预测和观测~同父异母的兄弟
实际系统中,我们可能有多个传感器给予我们关于系统状态的信息,我们这里不在乎其测量的量到底是什么,我们只要知道,每个传感器都间接地告诉了我们状态量。注意到我们预测状态量的尺度和单位和观测结果的尺度和单位可能是不一样的,这个时候就需要用线性变换把他们变成一样尺度和单位的。你可能猜到了,我们还是引入一个矩阵 H k \mathbf{H}_k Hk描述这个线性变换。
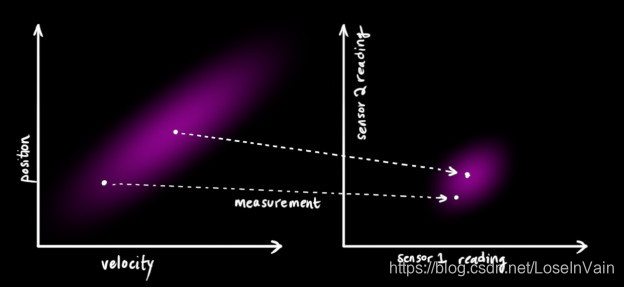
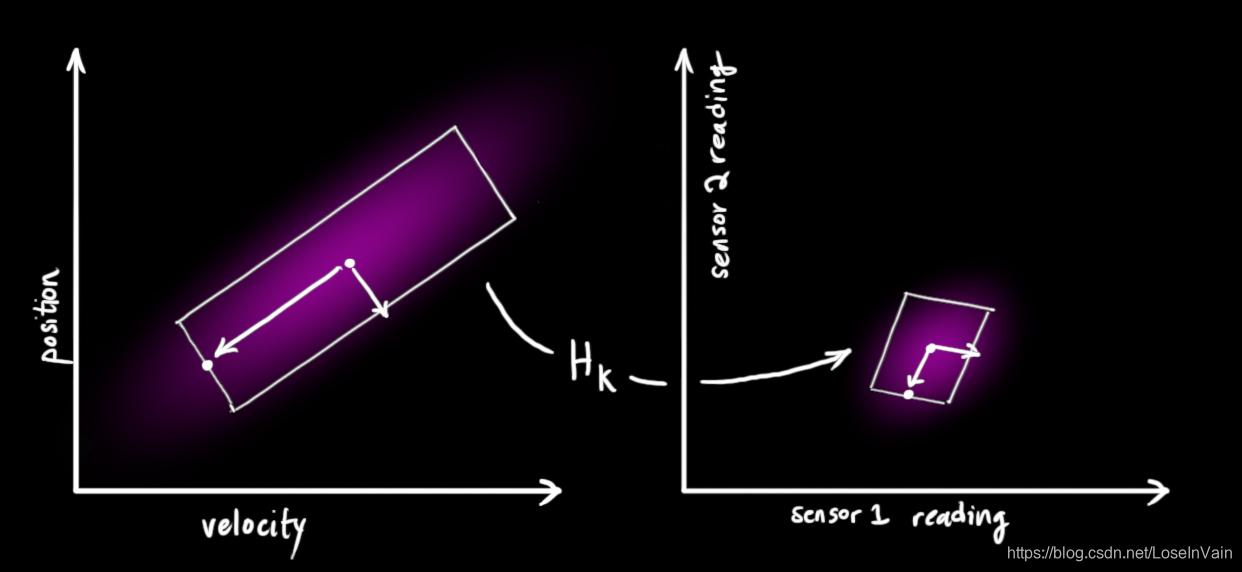
那么,公式有:
μ
⃗
e
x
p
e
c
t
e
d
=
H
k
x
^
k
Σ
e
x
p
e
c
t
e
d
=
H
k
P
k
H
k
T
(3.8)
\begin{aligned} \vec{\mu}_{\mathrm{expected}} &= \mathbf{H}_{k} \mathbf{\hat{x}}_{k} \\ \mathbf{\Sigma}_{\mathrm{expected}} &= \mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T \end{aligned} \tag{3.8}
μexpectedΣexpected=Hkx^k=HkPkHkT(3.8)
老问题,因为传感器存在噪声,我们的观测结果至少在某种程度上是不可靠的,在原来估计的情况下的结果可能对应了一个范围的传感器观测值。
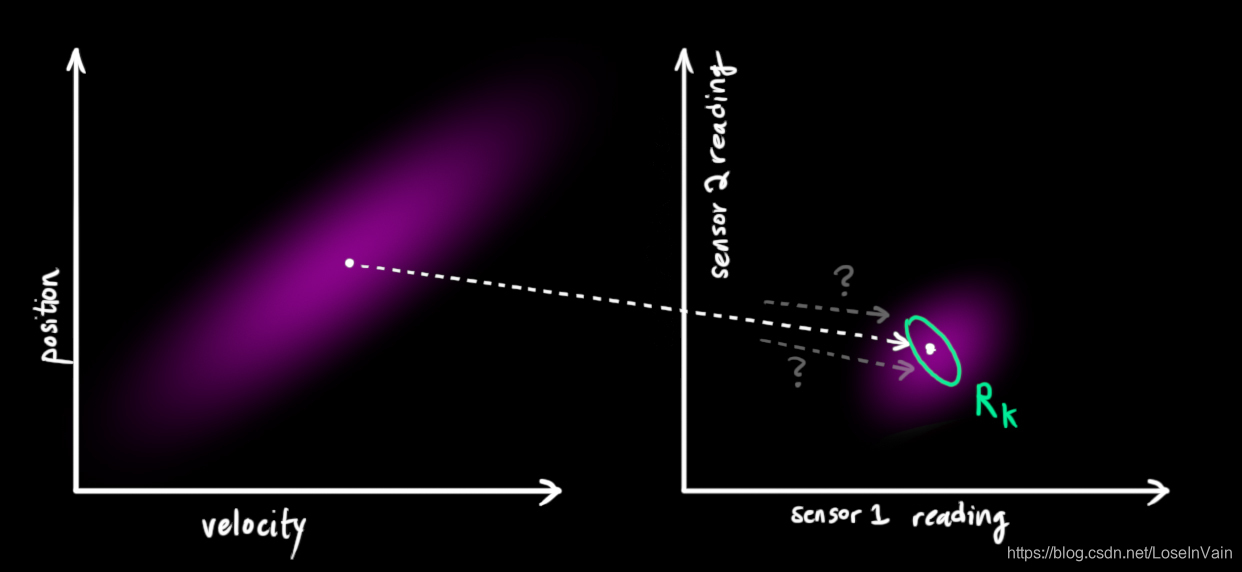
为了描述这个不确定性(也就是传感器噪声),我们引入了 R k \mathbf{R}_k Rk,这个分布的均值和我们的观测值 z k \mathbf{z}_k zk相同,但是存在有不确定性,用协方差进行描述。
到现在为止,我们有了两个高斯分布:
- 一个是通过线性变换 H k \mathbf{H}_k Hk 将预测结果转化为理论观察值的分布 H k x ^ k \mathbf{H}_k \mathbf{\hat{x}}_k Hkx^k。
- 另一个是实际的观察值的分布 R k \mathbf{R}_k Rk,其均值为 z k \mathbf{z}_k zk。
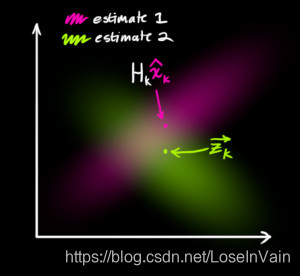
不难发现,因为这两个分布都是描述同一个量,其交集处,如Fig 12所示,应该是最好的估计结果,我们看到这个交集处,其协方差明显比观测和预测的都要小得多,结果也就更为精确。
为了得到这个交集分布的表达形式,我们需要将两个高斯分布进行相乘即可,我们知道高斯分布的乘积也是高斯分布[4]。

因此问题也就变成怎么求两个高斯分布的乘积的高斯分布的参数,如Fig 13所示:

根据[1,4]的推导,我们知道相乘后的结果为:
μ
′
=
μ
1
+
σ
1
2
(
μ
2
–
μ
1
)
σ
1
2
+
σ
2
2
(
σ
’
)
2
=
σ
1
2
–
σ
1
4
σ
1
2
+
σ
2
2
(3.9)
\begin{aligned} \mu^{\prime} &= \mu_1 + \frac{\sigma_1^2 (\mu_2 – \mu_1)} {\sigma_1^2 + \sigma_2^2}\\ (\sigma’)^2 &= \sigma_1^2 – \frac{\sigma_1^4} {\sigma_1^2 + \sigma_2^2} \end{aligned} \tag{3.9}
μ′(σ’)2=μ1+σ12+σ22σ12(μ2–μ1)=σ12–σ12+σ22σ14(3.9)
通过引入
K
\mathbf{K}
K,可以进行一些化简有:
K
=
σ
1
2
σ
1
2
+
σ
2
2
⇒
μ
′
=
μ
1
+
K
(
μ
2
−
μ
1
)
(
σ
′
)
2
=
σ
1
2
−
K
σ
1
2
(3.10)
\begin{aligned} \mathbf{K} &= \frac{\sigma_1^2}{\sigma_1^2 + \sigma_2^2} \\ \Rightarrow \\ \mu^{\prime} &= \mu_1 + \mathbf{K}(\mu_2-\mu_1) \\ (\sigma')^2 &= \sigma_1^2 - \mathbf{K} \sigma_1^2 \end{aligned} \tag{3.10}
K⇒μ′(σ′)2=σ12+σ22σ12=μ1+K(μ2−μ1)=σ12−Kσ12(3.10)
如果用矩阵形式表达,则有:
K
=
Σ
1
Σ
1
+
Σ
2
μ
′
⃗
=
μ
1
⃗
+
K
(
μ
2
⃗
−
μ
1
⃗
)
Σ
′
⃗
=
Σ
1
−
K
Σ
1
(3.11)
\begin{aligned} \mathbf{K} &= \dfrac{\Sigma_1}{\Sigma_1+\Sigma_2} \\ \vec{\mu'} &= \vec{\mu_1} + \mathbf{K}(\vec{\mu_2}-\vec{\mu_1}) \\ \vec{\Sigma'} &= \Sigma_1-\mathbf{K}\Sigma_1 \end{aligned} \tag{3.11}
Kμ′Σ′=Σ1+Σ2Σ1=μ1+K(μ2−μ1)=Σ1−KΣ1(3.11)
其中
Σ
1
,
Σ
2
\Sigma_1, \Sigma_2
Σ1,Σ2分别是预测和观测的协方差矩阵。其中如(2.4),我们把
K
\mathbf{K}
K称为卡尔曼增益,我们发现(3.11)和(2.4)形式上是一致的。
结合起来吧~状态更新
我们现在有两个分布了:
- 预测分布:
μ 1 ⃗ = H k x ^ k Σ 1 = H k P k H k T (3.12) \begin{aligned} \vec{\mu_1} = \mathbf{H}_k \mathbf{\hat{x}}_k \\ \Sigma_1 = \mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T \end{aligned} \tag{3.12} μ1=Hkx^kΣ1=HkPkHkT(3.12)
- 观测分布:
μ 1 ⃗ = z k Σ 1 = R k (3.13) \begin{aligned} \vec{\mu_1} = \mathbf{z}_k \\ \Sigma_1 = \mathbf{R}_k \end{aligned} \tag{3.13} μ1=zkΣ1=Rk(3.13)
将(3.12) (3.13)代入(3.11),我们有:
H
k
x
^
′
k
=
H
k
x
^
k
+
K
(
z
k
−
H
k
x
^
)
H
k
P
′
k
H
k
T
=
H
k
P
k
H
k
T
−
K
H
k
P
k
H
k
T
(3.14)
\begin{aligned} \mathbf{H}_k \mathbf{\hat{x}'}_k &= \mathbf{H}_k \mathbf{\hat{x}}_k + \mathbf{K}(\mathbf{z}_k - \mathbf{H}_k \mathbf{\hat{x}}) \\ \mathbf{H}_k \mathbf{P'}_k \mathbf{H}_k^T &= \mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T - \mathbf{K} \mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T \end{aligned} \tag{3.14}
Hkx^′kHkP′kHkT=Hkx^k+K(zk−Hkx^)=HkPkHkT−KHkPkHkT(3.14)
注意到(3.14)的
H
k
\mathbf{H}_k
Hk可以进行约减,最后得到:
x
′
^
k
=
x
^
k
+
K
′
(
z
k
−
H
k
x
^
k
)
P
′
k
=
P
k
−
K
′
H
k
P
k
(3.15)
\begin{aligned} \mathbf{\hat{x'}}_k &= \mathbf{\hat{x}}_k + \mathbf{K'}(\mathbf{z}_k-\mathbf{H}_k\mathbf{\hat{x}}_k) \\ \mathbf{P'}_k &= \mathbf{P}_k - \mathbf{K'} \mathbf{H}_k \mathbf{P}_k \end{aligned} \tag{3.15}
x′^kP′k=x^k+K′(zk−Hkx^k)=Pk−K′HkPk(3.15)
其中,卡尔曼增益变为:
K
′
=
P
k
H
k
T
H
k
P
k
H
k
T
+
R
k
\mathbf{K'} = \dfrac{\mathbf{P}_k\mathbf{H}_k^T}{\mathbf{H}_k \mathbf{P}_k\mathbf{H}_k^T+\mathbf{R}_k}
K′=HkPkHkT+RkPkHkT
这样,我们就得到了最后的结合了观测和模型预测的最佳估计
x
′
^
k
\mathbf{\hat{x'}}_k
x′^k了,并且知道了
P
′
k
\mathbf{P'}_k
P′k,可以为下一步的迭代更新提供先验了。我们发现,其实观测为预测提供了先验知识。这个过程可以一直迭代更新。整个卡尔曼滤波的流程如Fig 14所示。

Reference
[1]. https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
[2]. https://towardsdatascience.com/kalman-filter-intuition-and-discrete-case-derivation-2188f789ec3a
[3]. Pei Y, Biswas S, Fussell D S, et al. An elementary introduction to kalman filtering[J]. arXiv preprint arXiv:1710.04055, 2017.
[4]. http://www.tina-vision.net/docs/memos/2003-003.pdf

























 914
914

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










