机器学习实验七——PCA

最新推荐文章于 2024-09-10 18:37:45 发布

LouYou_

最新推荐文章于 2024-09-10 18:37:45 发布

阅读量965

点赞数 26

文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/LouYou_/article/details/139607741

版权

一、PCA概述

1.定义

PCA(Principal Component Analysis),称主成分分析,是一个非监督的机器学习算法。PCA通过将多个变量通过线性变换以选出较少的重要变量。它往往可以有效地从过于“丰富”的数据信息中获取最重要的元素和结构,去除数据的噪音和冗余,将原来复杂的数据降维,揭示隐藏在复杂数据背后的简单结构。

2.示例

例如各个国家可以在不同特征上进行区分，而国家可以从大量的特征方面进行分析，我们可以将大量特征降维到两个主要特征是进行分析：

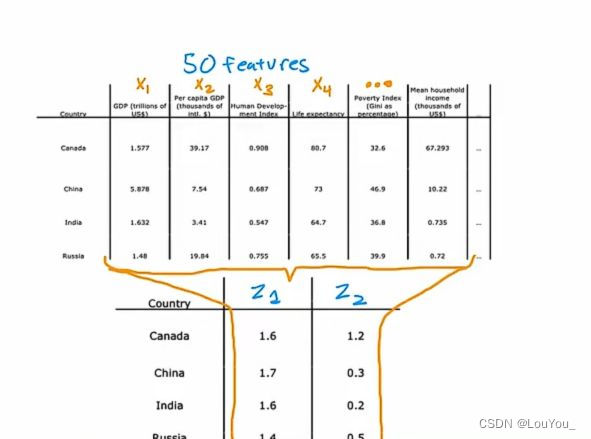
将x1、x2.....xn共50个特征映射到最主要的两个特征z1(国家GDP)、z2(人均GDP)上可以得到：

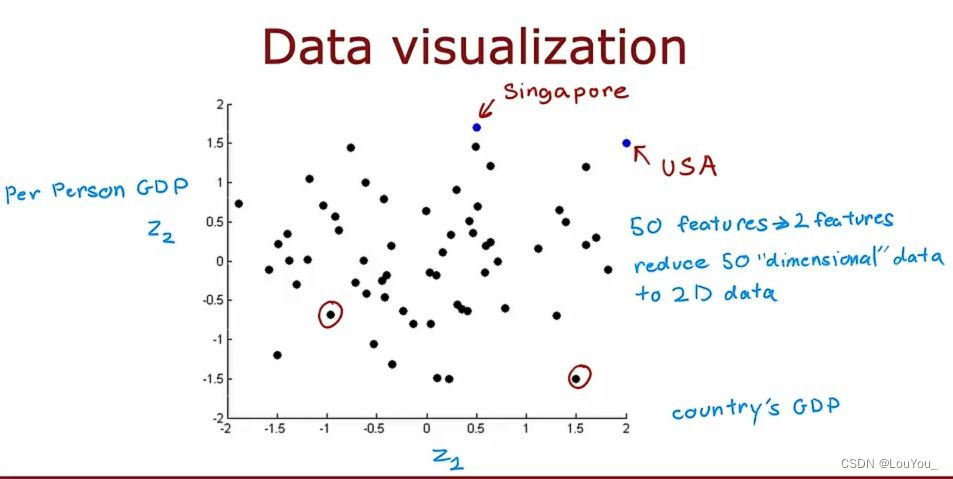
有效地减少数据的维度，同时尽可能保留原始数据中的重要信息

二、PCA原理

通过投影的方式，将高维的数据映射到低维的空间中，并且保证在所投影的维度上原数据的信息量最大，从而使用较少的数据维度保留住较多的原始数据特性。那么为了达成这个目的，PCA可以基于两种思路进行优化：

最大可分性：样本投影到低维的超平面之后能够尽量地分开。

例如：将图中的点分别映射到M轴和N轴上，映射到M轴上的样本数据明显比投影到N的样本数据更加分散。

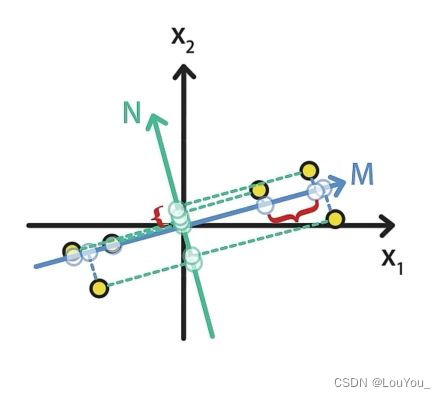
最近重构性：样本到待投影的低维超平面的距离要尽量的小

例如：平面上的样本到M的距离是蓝色线段，到N的距离是绿色线段

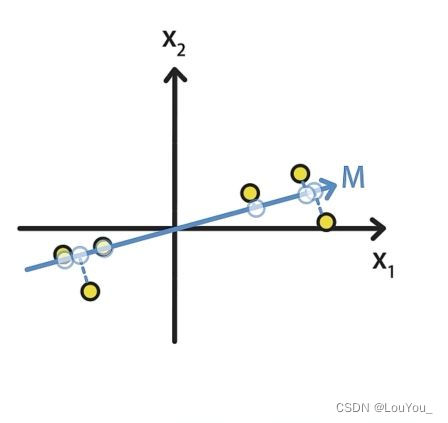
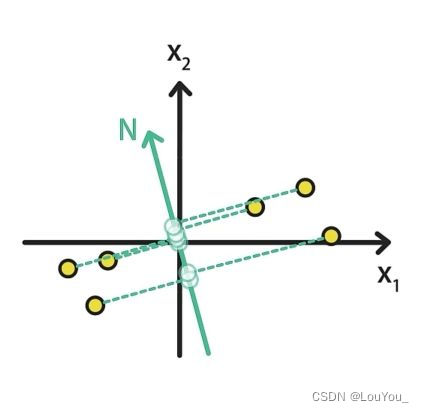
显而易见，蓝色距离之和小于绿色距离之和，所以M在最近重构性方面更好。

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。现在以两个特征的降维为例进行阐述：

例如汽车尺寸为例，以汽车的长度length和汽车的高度height为两个特征进行降维

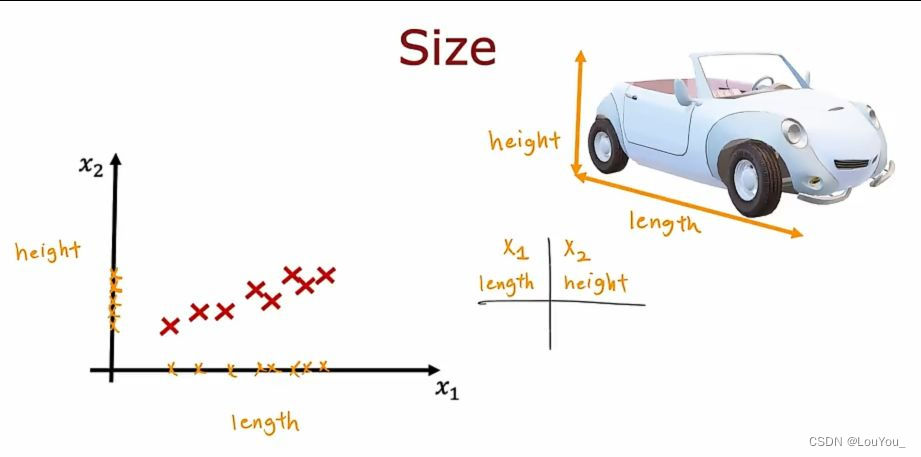
如图，将样本点映射到length特征上明显比映射到height上更为分散，所以若要降维在x1和x2中选一个，那必然是x1.

但是，height对汽车影响也较大。如果想要减少特征数量，又不想只选择x1而忽略了x2，可以考虑第三个轴而不是局限于采用x1轴或x2轴，如下图中z轴，代表汽车尺寸，用坐标到原点的长度作为特征值，将两个特征值降到了一个特征值，并且这个特征同时能反映height和length影响。

将样本点投影到z轴上也同时能满足最大可分性、最近重构性。

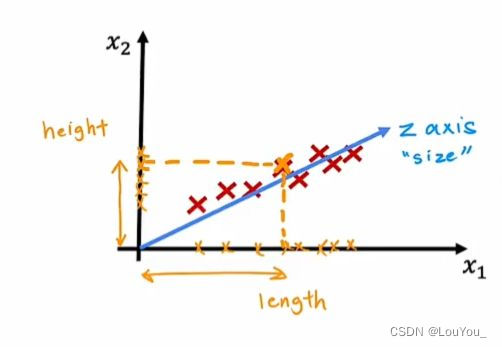
如何找到让样本间距最大的轴？

一般，会使用方差来定义样本之间的间距：

$Var(x)=\frac{1}{m}\sum_{i=1}^{m}(x_{i}-\bar{x})^{2}$

三、PCA求解过程

假设有m个样本，每个样本有n个特征那么样本集X为:

$X=\begin{bmatrix} X_{11} & X_{12}& ...& X_{1n}\\ X_{21}& X_{22}& ...& X_{2n}\\ ...& ...& ...& ...\\ X_{m1}& X_{m2}& ...& X_{mn} \end{bmatrix}$

现在欲将X={x1,x2...xn}降到k维，具体过程如下：

（1）去中心化

将数据集中的每个特征的值减去其均值，使得每个特征的均值变为0。

首先计算每列特征的均值 $\bar{_{xi}}$ ，其中xi为第i个特征：

$\bar{x_{i}}=\frac{1}{m}\sum_{j=1}^{m}x_{ji}$

接着让样本矩阵X中的每一个值进去其所在特征列对应的特征均值：

$X=\begin{bmatrix} x_{11}-\bar{x_{1}} & x_{12}-\bar{x_{2}}& ...& x_{1n}-\bar{x_{n}}\\ x_{21}-\bar{x_{1}} & x_{22}-\bar{x_{2}}& ...& x_{2n}-\bar{x_{n}}\\ ...& ...& ...& ...\\ x_{m1}-\bar{x_{1}} & x_{m2}-\bar{x_{2}}& ...& x_{mn}-\bar{x_{n}} \end{bmatrix}$

如下图所示为二维图像的去中心化示例：

首先，计算出样本的均值。

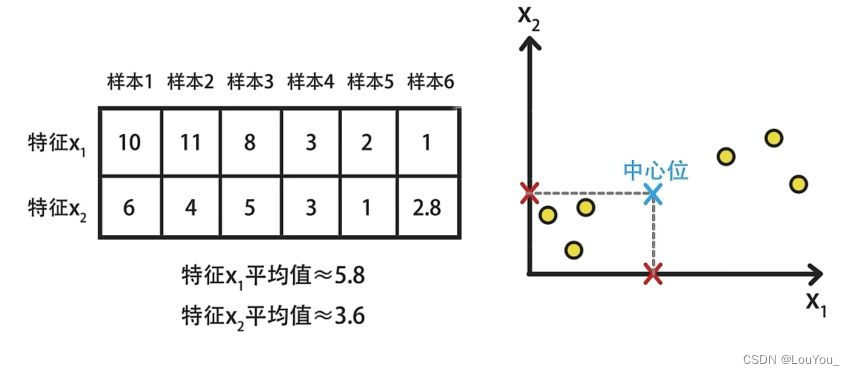
接着，样本对应的值减去均值（中心位移到了原点）实现图像去中心化。

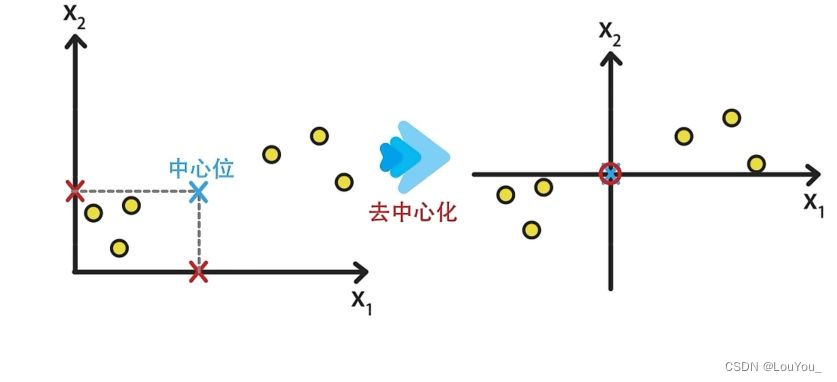
去中心化不会影响样本的分布性质，但会简化PCA算法的推导过程。

（2）计算协方差矩阵

$Cov=\frac{1}{m}X^{T}\cdot X$

Cov是一个n*n的矩阵。

计算数据的协方差矩阵，以了解数据特征之间的相关性。

（3）特征值和特征向量计算

求出协方差矩阵的特征值 $eq?%5Clambda%20_%7Bk%7D$ ，及对应的特征向量 $eq?v%20_%7Bk%7D$ ：

 $Cov\cdot V_{k}=\lambda _{k}V_{k}$

特征值和特征向量描述了数据在不同方向上的变异程度。

（4）选择主成分

根据特征值的大小，选择前几个最大的特征值对应的特征向量作为主成分。这些特征向量代表了数据中的主要变化方向：

将特征向量按对应特征值从左到右按列降序排列成矩阵，取前k列组成矩阵W（投影矩阵），即 $eq?n%5Ctimes%20k$

wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw==

阶矩阵。

（5）数据转换

将原始数据通过投影矩阵转换到主成分空间，得到新的数据集。这个新数据集的维度小于原始数据集，但保留了大部分的数据变异性：

通过 $eq?Y%3D%20XW$ 计算降维到k维后的样本特征，即 $eq?m%5Ctimes%20k$ 阶矩阵。

三、PCA算法代码实现

1.二维图像上寻找主成分方向

（1）获取样本集

1）代码实现

import numpy as np
import matplotlib.pyplot as plt
 
X=np.empty((100,2)) # 创建一个100行2列的空数组
X[:,0]=np.random.uniform(0,100,size=100) # 使用np.random.uniform函数填充数组的第一列，生成100个0到100之间的随机数
# 使用一个线性方程和噪声填充数组的第二列
# 0.6*X[:,0]是线性部分，表示第二列是第一列的0.6倍
# 3是线性方程的偏置项
# np.random.normal(0, 10, size=100)生成100个均值为0，标准差为10的正态分布随机数，作为噪声
X[:,1]=0.6*X[:,0]+3+np.random.normal(0,10,size=100)

利用函数np.random.uniform(0,100,size=100)随机获得一百个数作为X的第一个特征值，在通过线性+噪声的方式构造X的第二个特征。

2）运行结果

plt.scatter(X[:,0],X[:,1],marker='o', s=100, edgecolors='b')
plt.show()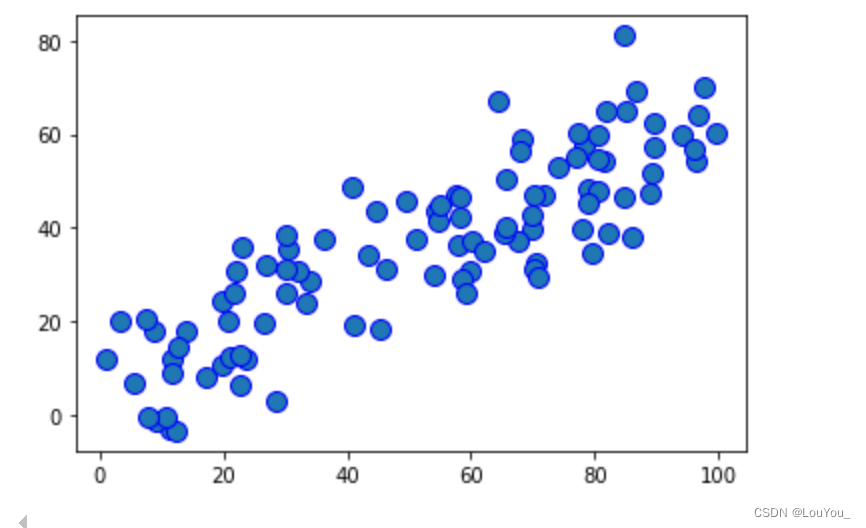

当前结果为初始的样本点分布，范围从0~100还未去中心化。

（2）去中心化

1）代码实现

#对数据进行中心化处理：减去每个特征的均值
def demean(X):
    return X-np.mean(X,axis=0) #将 X 中的每个元素减去对应的列均值

让样本矩阵X中的每一个元素减去其所在列的均值完成去中心化过程

2）运行结果

X_demean=demean(X)   #保存中心化后的数据
plt.xlim(-60, 60)  # 设置x轴的范围为0到100
plt.ylim(-60, 60)  # 设置y轴的范围为0到100
plt.scatter(X_demean[:,0],X_demean[:,1],marker='o', s=100, edgecolors='b')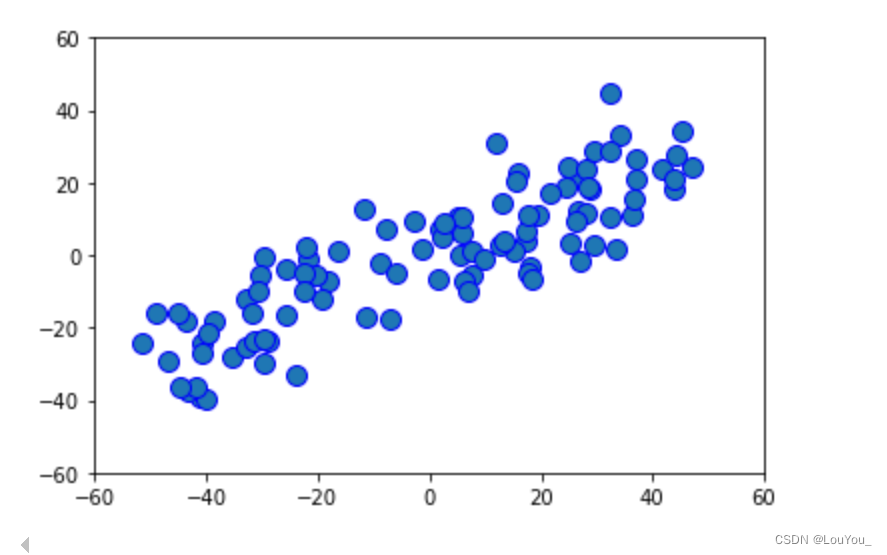

将数据集中的每个特征的值减去其均值，使得每个特征的均值变为0。经过去中心化后，原样本集的中心点移至原点（0，0）整个样本随之移动实现去中心化。

（3）找到主成分

1）代码实现

#定义目标函数：数据在投影到方向 w 上时的方差
#方向w为所要求的主成分方向，当方差最大时就是要求的主成分
#要做的就是找到使目标函数最大的w，可以通过梯度上升法实现
def f(w,X):
    return np.sum((X.dot(w)**2))/len(X)
 
#目标函数对w求偏导得到关于参数w的梯度
def gradient_f(w,X):
    return X.T.dot(X.dot(w))*2/len(X)
 
#梯度上升法求w    
def gradient_ascent(X, initial_w, learning_rate):
    
    w = initial_w
    n_iters = 500
 
    for i in range(n_iters):
        gradient = gradient_f(w, X) #得到关于w的梯度
        w = w + learning_rate * gradient #梯度上升  
    return w

首先，我们要找的主成分方向是要将数据投影到主成分方向上，而在这个主成分方向上的方差要是最大的。那么我们的目标函数就是 $f=\frac{1}{n}\sum_{i=1}^{n}(x_{i}\cdot w)^{2}$ ,其中w是我们欲求的主成分方向向量。

接着，根据这个目标函数目的是求其最大值，那么使得目标函数到达最大值的w向量就是我们所需要的主成分方向向量，那么我们就可以借助梯度上升方法来求解w。

2）运行结果

initial_w = np.random.random(X.shape[1]) # 生成与特征数相同的随机向量作为初始权重向量
learning_rate = 0.001
w = gradient_ascent(X_demean, initial_w, learning_rate)
plt.figure(3)
plt.xlim(-60, 60)  # 设置x轴的范围为0到100
plt.ylim(-60, 60)  # 设置y轴的范围为0到100
plt.scatter(X_demean[:,0], X_demean[:,1],marker='o', s=100, edgecolors='b')
plt.plot([0, w[0]*100], [0 , w[1]*100], color='r')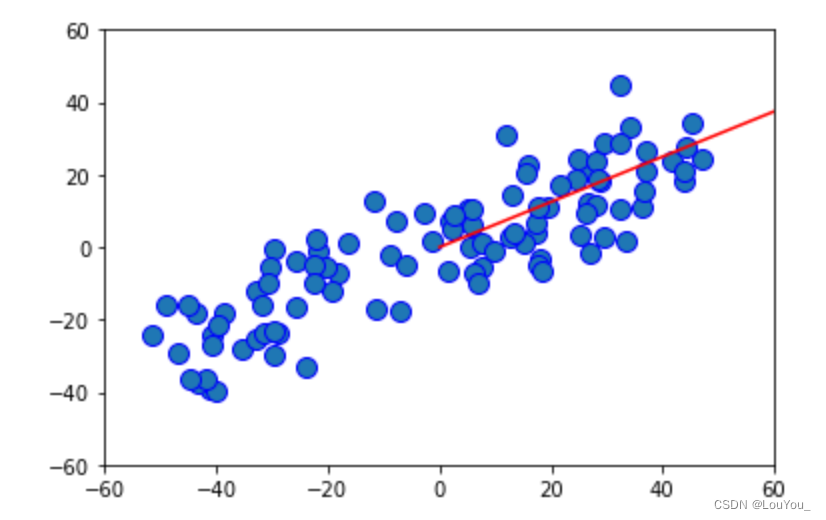

如图中红线所示即是我们所要求的主成分方向。

2.进行人脸数据压缩

（1）展示人脸数据

1）代码

# 导入numpy库，并给它起一个别名np，这是常见的做法。
import numpy as np

# 从numpy库中导入dot函数，用于计算向量的点积。
from numpy import dot

# 从scipy.io模块导入loadmat函数，用于加载MATLAB的.mat文件。
from scipy.io import loadmat

# 从sklearn.decomposition模块导入PCA类，用于执行主成分分析。
from sklearn.decomposition import PCA

# 导入numpy的线性代数模块，别名为linalg。
import numpy.linalg as linalg

# 导入matplotlib的pyplot模块，用于绘图，别名为plt。
import matplotlib.pyplot as plt

# 使用loadmat函数加载位于指定路径的.mat文件，并将结果存储在变量faces中。
faces = loadmat("D:\Anaconda\PythonTest\ex7faces.mat")

# 从加载的mat文件中提取名为'X'的变量，将其赋值给X。
X = faces['X']

# 打印变量X的形状，这将告诉我们数据集中有多少个样本，以及每个样本的特征数量。
print(X.shape)

# 定义一个函数plot_100_image，它接受一个参数X。
def plot_100_image(X):
    # 使用matplotlib创建一个10行10列的子图网格，整个图的大小为10x10英寸。
    fig, ax = plt.subplots(nrows=10, ncols=10, figsize=(10, 10))
    
    # 循环遍历每一行。
    for c in range(10):
        # 循环遍历每一列。
        for r in range(10):
            # 选择X中的图像，将其重新排列为32x32的矩阵，并进行转置，然后显示在相应的子图上。
            ax[c, r].imshow(X[10*c+r].reshape(32, 32).T, cmap='Greys_r')
            # 隐藏子图的x轴刻度。
            ax[c, r].set_xticks([])
            # 隐藏子图的y轴刻度。
            ax[c, r].set_yticks([])
    
    # 显示所有的子图。
    plt.show()

# 调用plot_100_image函数，并传入X作为参数，这将绘制100幅图像。
plot_100_image(X)

2）运行结果

展示了前一百张人脸图

（2）降维操作

1）代码

首先是要对数据进行去中心化处理

# 定义一个函数reduce_mean，用于计算数据集X的均值并减去该均值。
def reduce_mean(X):
    # 计算X的每列的均值，axis=0表示沿着列方向操作。
    # 然后从X中减去这个均值，得到中心化的数据集X_reduce_mean。
    X_reduce_mean = X - X.mean(axis=0)
    return X_reduce_mean

接着在去中心化后计算协方差矩阵

# 定义一个函数sigma_matrix，用于计算中心化数据集的协方差矩阵。
def sigma_matrix(X_reduce_mean):
    # 使用X_reduce_mean的转置与其自身的点积计算协方差矩阵。
    # 然后除以样本数量（X_reduce_mean的行数）得到标准化的协方差矩阵sigma。
    sigma = (X_reduce_mean.T @ X_reduce_mean) / X_reduce_mean.shape[0]
    return sigma

进行奇异值分解

# 定义一个函数usv，用于对协方差矩阵sigma进行奇异值分解。
def usv(sigma):
    # 使用numpy的线性代数模块linalg中的svd函数对sigma进行奇异值分解。
    # 返回分解得到的三个矩阵u, s, v。
    u, s, v = linalg.svd(sigma)
    return u, s, v

将数据投影到主成分上并用此恢复原始数据

# 定义一个函数project_data，用于将数据投影到主成分上。
def project_data(X_reduce_mean, u, k):
    # 从u矩阵中选择前k列，形成u_reduced矩阵。
    # 使用点积将中心化的数据集X_reduce_mean投影到这k个主成分上，得到投影后的z。
    u_reduced = u[:, :k]
    z = dot(X_reduce_mean, u_reduced)
    return z

# 定义一个函数recover_data，用于从投影后的z恢复原始数据。
def recover_data(z, u, k):
    # 同project_data函数一样，从u矩阵中选择前k列。
    # 使用点积将投影后的z恢复到原始数据空间，得到近似的X_recover。
    u_reduced = u[:, :k]
    X_recover = dot(z, u_reduced.T)
    return X_recover

2）运行结果

展示一百张降维之后的人脸图

四、实验总结

1.问题与解决

（1）问题1：协方差矩阵的计算错误

现象：在计算协方差矩阵时，由于对公式理解不深刻，出现了计算错误，影响了特征值和特征向量的求解。

解决方案：回顾协方差矩阵的定义和计算方法，确保使用正确的公式进行计算。同时，利用NumPy库中的函数来自动化计算过程，减少手动计算的错误。

（2）问题2：梯度上升法的实现不稳定

现象：在实现梯度上升法寻找主成分方向时，遇到了收敛速度慢或不收敛的问题。

解决方案：调整学习率。同时，增加对梯度上升过程中的监控，确保算法能够收敛到合适的主成分方向。

（3）问题3：数据标准化处理不足

现象：实验中发现，原始数据的量纲和数值范围差异较大，未进行适当的标准化处理，导致PCA结果偏差。

解决方案：在进行PCA之前，对每个特征进行标准化处理，确保每个特征对PCA结果的贡献是均等的。

2.实验小结

PCA有效性：PCA能够有效地从高维数据中提取出最重要的特征，降低数据的维度，同时尽可能地保留原始数据的信息。

降维效果：通过对比原始数据和降维后的数据，发现PCA在减少数据维度的同时，仍然能够较好地保持数据的基本结构。

主成分的重要性：实验中观察到，选择的主成分数量对降维效果有显著影响，适量的主成分可以平衡降维和数据保持度。

通过本次实验，我们深入理解了PCA的工作原理和实现方法，并成功将其应用于数据降维和特征提取。PCA作为一种有效的数据预处理技术，在数据压缩、去噪和模式识别等领域具有广泛的应用前景。实验结果表明，PCA能够在降低数据维度的同时，有效地保留数据的重要信息，是一种值得推广的数据处理方法。

LouYou_

关注

26
点赞
踩
17

收藏

觉得还不错? 一键收藏
0
评论
机器学习实验七——PCA

PCA(Principal Component Analysis),称主成分分析,是一个非监督的机器学习算法。PCA通过将多个变量通过线性变换以选出较少的重要变量。它往往可以有效地从过于“丰富”的数据信息中获取最重要的元素和结构,去除数据的噪音和冗余,将原来复杂的数据降维,揭示隐藏在复杂数据背后的简单结构。现象：在计算协方差矩阵时，由于对公式理解不深刻，出现了计算错误，影响了特征值和特征向量的求解。解决方案：回顾协方差矩阵的定义和计算方法，确保使用正确的公式进行计算。
复制链接

扫一扫