机器学习实验五——logistic回归模型

最新推荐文章于 2024-06-15 20:14:26 发布

LouYou_

最新推荐文章于 2024-06-15 20:14:26 发布

阅读量1k

点赞数 31

文章标签：机器学习回归人工智能

本文链接：https://blog.csdn.net/LouYou_/article/details/139217681

版权

一、逻辑回归概述

逻辑回归是统计学中的一种回归模型，它被广泛用于二分类问题。尽管名字中有“回归”二字，逻辑回归实际上是一种分类算法。以下是逻辑回归的概述介绍：

1.定义：

逻辑回归是一种预测分析方法，用于估计一个特定事件的发生概率。它通过使用逻辑函数（通常是Sigmoid函数）将线性回归模型的输出映射到0和1之间，从而实现对二元分类问题的预测。

2.基本原理：

线性组合：逻辑回归首先计算输入特征的线性组合，即 z=w1x1+w2x2+...+wnxn+b，其中 w 是权重，b 是偏置项，x 是特征值。
Sigmoid函数：将线性组合的输出 z 通过Sigmoid函数转换，得到 $f(z)=\frac{1}{1+e^{-z}}$ 。这个函数的输出范围在0到1之间，可以被解释为概率。
概率解释：Sigmoid函数的输出可以被解释为样本属于分类“1”的概率。如果这个概率超过某个阈值（通常是0.5），则预测样本为“1”，否则预测为“0”。

3.代价函数：

逻辑回归使用对数损失或交叉熵损失作为代价函数，用于衡量模型预测的概率分布与实际标签之间的差异。代价函数的形式为：

$J(w)=-\frac{1}{m}\sum_{1}^{m}(yi*log(f(zi))+(1-yi)*log(1-f(zi)))$

其中，m 是样本数量，yi 是第 i 个样本的真实标签，zi 是第 i 个样本的线性组合输出。

4.优化算法：

通常使用梯度下降（Gradient Descent）或其变体（如随机梯度下降Stochastic Gradient Descent, SGD）来最小化代价函数，从而找到最优的权重 w 和偏置 b。

5.优缺点：

优点：模型简单，易于理解和实现；可以提供分类的概率解释；计算效率较高。
缺点：假设特征和输出之间是线性关系，可能不适用于所有数据集；对于非线性问题，需要进行特征工程；在特征空间很多维度时，性能可能下降。

逻辑回归是一种强大的工具，尤其适用于二分类问题，并且可以扩展到多分类问题（如多项逻辑回归）。通过适当的特征选择和工程，逻辑回归可以提供准确的预测和洞察。

二、逻辑回归模型构造

1.需求

逻辑回归模型可以看成是线性回归+sigmoid函数

线性回归：z=w*x+b

sigmoid函数: y=1/(1+e^(-z))

逻辑回归：y=1/(1+e^(-w*x+b))

所以求解一个好的逻辑回归只需要求解最佳的w和b即可

2.代价函数

1）代价函数是体现“预测值”与“实际值”相似程度的函数

2）代价函数越小，模型越好

线性回归的代价函数： $J(w,b)=\frac{1}{m}\sum_{1}^{m}(f_{w,b}(xi)-yi)^{2}$

若逻辑回归也是采用此代价函数，可如下图所示：

逻辑回归的代价函数将会是非凸代价函数不凸，意味着如果尝试使用梯度下降可能会陷入很多局部最小值。所以平方误差代价函数对逻辑回归来说不是一个好的选择

逻辑回归的代价函数有不一样的代价函数，使得代价函数再凸：

简化版Loss：

$L(f(xi),yi)=-yi*log(f(xi))-(1-yi)log(1-f(xi))$

简化后Cost：

$J(w,b)=-\frac{1}{m}\sum_{1}^{m}[yi*log(f(xi))+(1-yi)*log(1-f(xi))]$

在求解逻辑回归模型中，就只用找到最佳的w和b使得J(w,b)最小即可

3.梯度下降

梯度下降是一种优化算法，用于最小化一个函数，特别是指代价函数或损失函数。

（1）基本原理

梯度下降算法通过迭代过程来寻找函数的局部最小值。它的核心思想是，通过计算函数的梯度（即导数）来确定函数增长最快的方向，然后向相反方向更新变量（如模型参数），以此逐步逼近函数的最小值。

（2）关键步骤

1）初始化参数：选择一个初始点作为模型参数的起始值。

2）计算梯度：计算当前参数下损失函数的梯度，即损失函数对每个参数的偏导数。

3）参数更新：根据梯度和一个预先设定的学习率（步长）来更新参数。参数更新的公式通常是： $\Theta _{new}=\Theta _{old}-\eta \cdot \triangledown J(\Theta _{old})$ ，其中 θ 是参数，η 是学习率，∇J 是损失函数 J 的梯度。

4）迭代：重复步骤2和3，直到满足停止条件，如梯度足够小、达到预定的迭代次数或损失函数值不再显著减小。

（3）学习率的选择

较小的学习率：可能导致收敛速度慢。
较大的学习率：可能导致跳过最小值甚至发散。

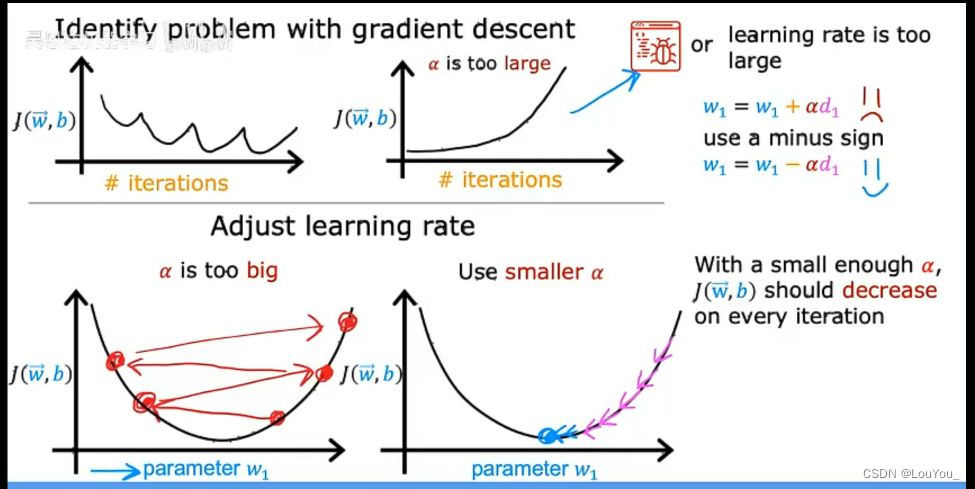
（4）变体梯度下降有几种变体，以适应不同的优化场景：

批量梯度下降（Batch Gradient Descent）：使用整个数据集来计算每次迭代的梯度。
随机梯度下降（Stochastic Gradient Descent, SGD）：每次迭代只使用一个训练样本来更新参数。

在这次logistic回归模型构建中利用梯度下降算法对w和b进行更新，更新的表达式如下：

$w_{j}=w_{j}-\alpha [\frac{1}{m}\sum_{1}^{m}(f(xi)-yi)*x_{j}^{i}]$

$b=b-\alpha [\frac{1}{m}\sum_{1}^{m}(f(xi)-yi)]$

三、具体实现

1.收集数据

-0.017612	14.053064	0
-1.395634	4.662541	1
-0.752157	6.538620	0
-1.322371	7.152853	0
0.423363	11.054677	0
0.406704	7.067335	1
0.667394	12.741452	0
-2.460150	6.866805	1
0.569411	9.548755	0
-0.026632	10.427743	0
0.850433	6.920334	1
1.347183	13.175500	0
1.176813	3.167020	1
-1.781871	9.097953	0
-0.566606	5.749003	1
0.931635	1.589505	1
-0.024205	6.151823	1
-0.036453	2.690988	1
-0.196949	0.444165	1
1.014459	5.754399	1
1.985298	3.230619	1
-1.693453	-0.557540	1
-0.576525	11.778922	0
-0.346811	-1.678730	1
-2.124484	2.672471	1
1.217916	9.597015	0
-0.733928	9.098687	0
-3.642001	-1.618087	1
0.315985	3.523953	1
1.416614	9.619232	0
-0.386323	3.989286	1
0.556921	8.294984	1
1.224863	11.587360	0
-1.347803	-2.406051	1
1.196604	4.951851	1
0.275221	9.543647	0
0.470575	9.332488	0
-1.889567	9.542662	0
-1.527893	12.150579	0
-1.185247	11.309318	0
-0.445678	3.297303	1
1.042222	6.105155	1
-0.618787	10.320986	0
1.152083	0.548467	1
0.828534	2.676045	1
-1.237728	10.549033	0
-0.683565	-2.166125	1
0.229456	5.921938	1
-0.959885	11.555336	0
0.492911	10.993324	0
0.184992	8.721488	0
-0.355715	10.325976	0
-0.397822	8.058397	0
0.824839	13.730343	0
1.507278	5.027866	1
0.099671	6.835839	1
-0.344008	10.717485	0
1.785928	7.718645	1
-0.918801	11.560217	0
-0.364009	4.747300	1
-0.841722	4.119083	1
0.490426	1.960539	1
-0.007194	9.075792	0
0.356107	12.447863	0
0.342578	12.281162	0
-0.810823	-1.466018	1
2.530777	6.476801	1
1.296683	11.607559	0
0.475487	12.040035	0
-0.783277	11.009725	0
0.074798	11.023650	0
-1.337472	0.468339	1
-0.102781	13.763651	0
-0.147324	2.874846	1
0.518389	9.887035	0
1.015399	7.571882	0
-1.658086	-0.027255	1
1.319944	2.171228	1
2.056216	5.019981	1
-0.851633	4.375691	1
-1.510047	6.061992	0
-1.076637	-3.181888	1
1.821096	10.283990	0
3.010150	8.401766	1
-1.099458	1.688274	1
-0.834872	-1.733869	1
-0.846637	3.849075	1
1.400102	12.628781	0
1.752842	5.468166	1
0.078557	0.059736	1
0.089392	-0.715300	1
1.825662	12.693808	0
0.197445	9.744638	0
0.126117	0.922311	1
-0.679797	1.220530	1
0.677983	2.556666	1
0.761349	10.693862	0
-2.168791	0.143632	1
1.388610	9.341997	0
0.317029	14.739025	0

数据集前两项为特征值，最后一项为数据对应类别标签

（1）代码：

#1.收集数据
def datas():
    rdata=[]
    fr=open(r"C:\Users\86180\Desktop\logistic_test.txt")
    for line in fr.readlines():
        temp=line.strip().split()
        rdata.append([float(temp[0]),float(temp[1]),int(temp[2])])
    return rdata

def dataset():
    data=datas()
    for row in data:
        row.insert(0, int(1))  #在训练数据加入新一列并全都设为1，可以认为是方便后面的计算直接把这列值与其对应的权重相乘当作b
    data=np.array(data)
    x = data[:,0:len(data[0])-1] #存放特征值
    y = data[:,-1]    #存放正确答案即正确标签
    w=np.zeros(len(x[0])) #存放权重，即wx+b中的w
    return x,y,w

在data中添加一列值为1作为偏置项（用于求b）

（2）运行结果：

利用如下代码可视化样本散点分布情况

data=datas()
positive = []
negative = []
for i in data:
        if i[2] == 1:
            positive.append(i[:2])  # 只添加前两个特征值
        else:
            negative.append(i[:2])  # 只添加前两个特征值
positive = list(zip(*positive))  # 转置以便绘图
negative = list(zip(*negative))  # 转置以便绘图
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive[0], positive[1], s=50, c='b', marker='o', label='1')
ax.scatter(negative[0], negative[1], s=50, c='r', marker='x', label='0')
ax.legend()
ax.set_xlabel('feature1')
ax.set_ylabel('feature2')
plt.show()

dataset函数中所返回的值x是两个特征和一个偏置项1，y是类别标签，w是初始权重

x,y,w=dataset()
print(x)
print(y)
print(w)

打印结果如下：

部分x:

w:（初始化为0）

2.Sigmoid函数

（1）代码：

#sigmoid函数
def sigmoid(z):
    return 1.0/(1+np.exp(-z))

按照Sigmoid函数公式实现这部分代码

（2）运行结果：

nums = np.arange(-20, 20, step=1)
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(nums, sigmoid(nums), 'r')
plt.show()

在-20到20范围内绘制sigmoid函数图像：

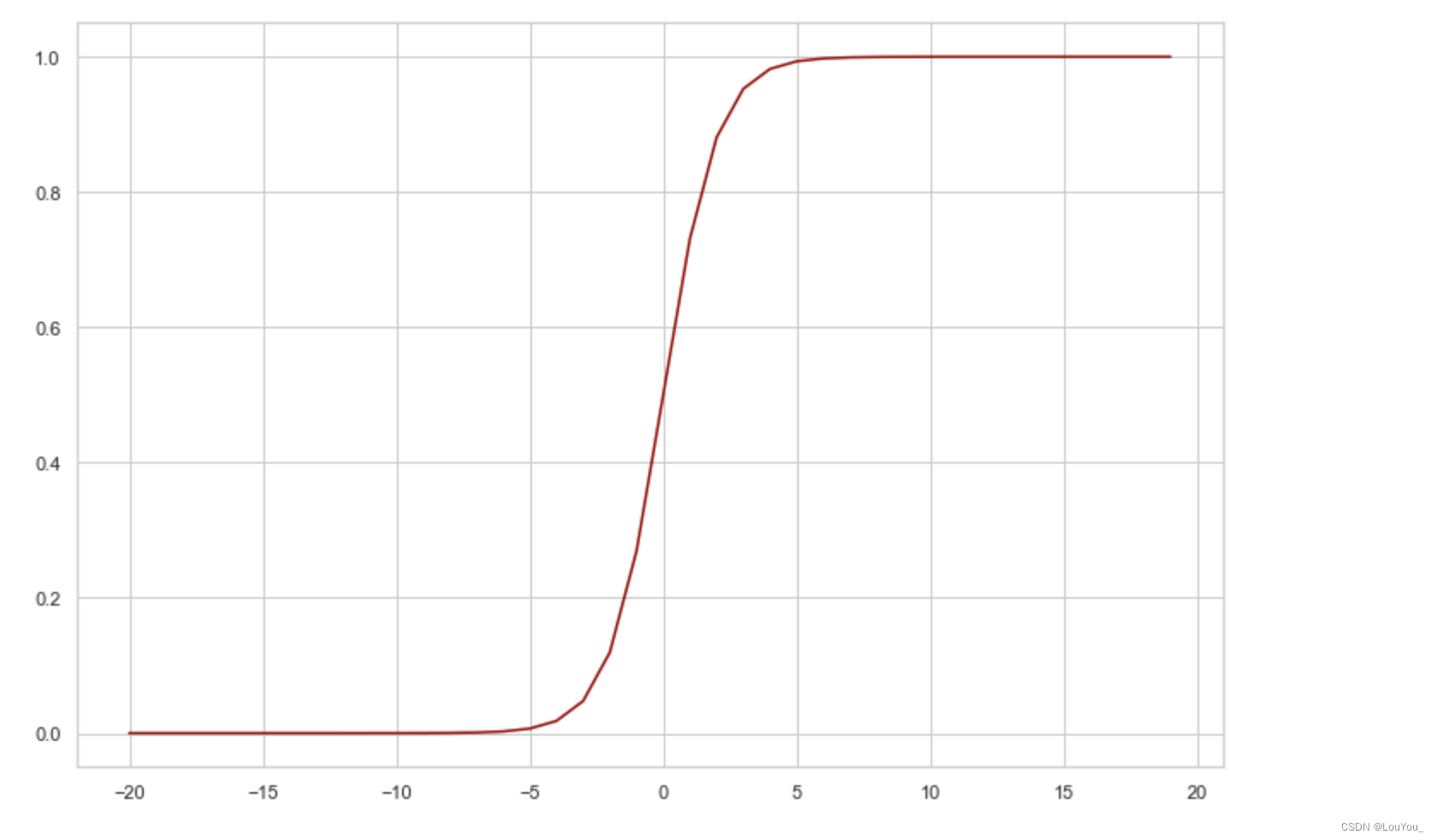
Sigmoid函数当x=0时值为0.5，当x趋于负无穷时值趋于0，当x趋于正无穷时值趋于1。在逻辑回归中，将线性wx+b结果代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

3.代价函数

（1）代码：

#计算代价函数
def cost(x,y,w):
    first = np.multiply(-y, np.log(sigmoid(x @ w.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(x @ w.T)))
    return np.sum(first - second) / (len(x))

根据此前的J(w,b)公式设计代价函数

（2）运行结果：

x,y,w=dataset()
print(cost(x,y,w))

计算一下未经优化时的初始代价：

4.梯度下降函数

（1）代码：

#由于x第一列具体值都相同为一个常数，可以把这一列的值与其对应的w0相乘作为b
def gradient_descent(x,y,w):
    a=0.001  #学习率
    _x=np.mat(x) #将x、y、w转换成矩阵进行计算
    _y=np.mat(y).transpose()    #y和w需要转置来匹配运算规则
    _w=np.mat(w).transpose()
    cost_data=[cost(np.array(_x),np.array(_y),np.array(_w.T))]  #存放每次迭代后的代价大小
    for i in range(501):
        _w=_w-a*(_x.T@(sigmoid(_x@_w)-_y))  #其中sigmoid(_x@_w)是预测值,_y是实际值，根据梯度下降的更新规则对权重_w进行更新
        cost_data.append(cost(np.array(_x),np.array(_y),np.array(_w.T)))
    return _w,cost_data

其中变量a是学习率，来控制变更的大小，选择过大或过小对最终的结果都有较大影响。过小使得变化收敛太慢，过大使得跳过最小值造成代价忽大忽小。其他思路如图中注释。

（2）运行结果：

最终的权重w：

w0=3.90923018, w1=0.46127407, w2=-0.58980953

每一轮迭代的cost_data:

可见代价在每次迭代的过程中不断降低最终达到了0.194的比较好的结果，将代价变化可视化如下：

_w,cost_data=gradient_descent(x,y,w)
ax = sns.lineplot(x=np.arange(502), y=cost_data)
ax.set_xlabel('epoch')
ax.set_ylabel('cost')
plt.title('Cost Function History')
plt.show()

可以看到随着迭代次数的增加，cost也逐渐降低，第一轮变化最明显，其后缓缓降低。

5.绘制决策边界

（1）代码：

def plotBestFit(weights):
    dataMat, labelMat,w = dataset()      
    dataArr = np.array(dataMat)      
    n = np.shape(dataArr)[0]     # 获取数据总数
    xcord1 = []; ycord1 = []       # 存放正样本
    xcord2 = []; ycord2 = []       # 存放负样本
    for i in range(n):                                     # 依据数据集的标签来对数据进行分类
        if int(labelMat[i]) == 1:                          # 数据的标签为1，表示为正样本
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:      
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='b', marker='o')  # 绘制正样本
    ax.scatter(xcord2, ycord2, s=30, c='r', marker='x')      # 绘制负样本     
    x = np.arange(-3, 3, 0.1)      
    y = (-weights[0,0] - weights[1,0] * x) / weights[2,0]    
    ax.plot(x, y)
    plt.title('cxr_test')          
    plt.xlabel('X1'); plt.ylabel('X2')
    plt.legend(["1","0","decision boundary"])
    plt.show()

（2）运行结果：

dataMat, labelMat,w = dataset()
weigths,cost_data = gradient_descent(dataMat, labelMat,w)
weigths=np.array(weigths)
plotBestFit(weigths)

这次实践获得的决策边界较好，只有几个点不符合决策边界的划分情况。

6.预测测试

（1）代码

def predict(inX, weights):
    prob = sigmoid(sum(inX * weights))
    #大于0.5 返回 1；否则返回0
    if prob > 0.5:
        return 1.0
    else:
        return 0.0

根据梯度下降函数得到的最终权重大小和传入的预测样本进行计算，当计算结果prob大于0.5时就表示该样本更可能是了类别‘1’，将其分入类别‘1’。

（2）运行结果：

dataMat, labelMat,w = dataset()
weigths,cost_data = gradient_descent(dataMat, labelMat,w)
inx=[1,-0.196949,0.444165]
weigth=[weigths[0,0],weigths[1,0],weigths[2,0]]
inx=np.array(inx)
weigth=np.array(weigth)
print("该样本类别为：",predict(inx,weigth))

传入样本inx第一个值为偏置项1，剩余两个为特征值，该样本的实际类别为‘1’

用weigth存放得到的三个权重

将inx、weigth换为numpy数组带入predicct函数进行计算

预测结果得到：

与实际类别相符，预测正确

四、总结

1.问题与解决

（1）问题：被如何同时更新w和b来获得最佳的w、b所困扰

解决：观看教学视频以及网络查询，发现在data数据集第一列新增一列作为偏置项，其初始值为1，在初始w时对应的w0将对这个偏置项进行更新，最后的w0可以作为我们要的b。

（2）问题：在梯度下降函数中查看每次的代价有时候是逐渐增大，有时候是突然增大突然减少

解决：观看教学视频发现是学习率Alpha对更新的影响，开始时我的学习率Alpha设置过大造成了这种情况的发生，在多次尝试不同的学习率后找到一个较为可行的值作为实验所需的学习率。

（1）问题：numpy数组与矩阵的运算规则不清

解决：网上查阅学习，明白了对于二维数组，* 运算符执行的是逐元素相乘，而 @ 运算符执行的是矩阵乘法。矩阵乘法的要求是左侧矩阵的列数必须等于右侧矩阵的行数。对于一维数组，* 运算符执行的也是逐元素相乘。

2.实验小结

理解逻辑回归：逻辑回归虽然名字中有“回归”二字，但它实际上是一种分类算法，特别是用于二分类问题。通过使用Sigmoid函数将线性回归的输出映射到0和1之间，逻辑回归能够预测特定事件发生的概率。

模型构建：在构建逻辑回归模型时，我们首先需要定义模型的形式，即线性回归加上Sigmoid函数。然后，我们需要定义一个合适的代价函数来衡量模型预测与实际标签之间的差异。在本实验中，我们使用了对数损失或交叉熵损失作为代价函数。

梯度下降算法：为了找到最优的权重和偏置项，我们使用了梯度下降算法。通过迭代地更新参数，我们能够最小化代价函数，从而得到最佳的模型参数。实验中，我们发现学习率的选择对模型的收敛速度和最终结果有重要影响。

实验体会：通过本次实验，我们深刻体会到了逻辑回归在二分类问题中的应用，以及如何通过编程实现机器学习算法。我们也认识到了选择合适的学习率和理解矩阵运算规则的重要性。此外，实验过程中的问题解决让我们更加熟悉了机器学习模型的调试和优化过程。总的来说，本次实验不仅加深了我们对逻辑回归的理解，也提高了我们的编程能力和问题解决能力。通过实践，我们学会了如何构建、训练和评估一个逻辑回归模型，这是我们在数据科学和机器学习领域的重要一步。

LouYou_

关注

31
点赞
踩
11

收藏

觉得还不错? 一键收藏
0
评论
机器学习实验五——logistic回归模型

逻辑回归是统计学中的一种回归模型，它被广泛用于二分类问题。尽管名字中有“回归”二字，逻辑回归实际上是一种分类算法。逻辑回归是一种预测分析方法，用于估计一个特定事件的发生概率。它通过使用逻辑函数（通常是Sigmoid函数）将线性回归模型的输出映射到0和1之间，从而实现对二元分类问题的预测。2.基本原理：线性组合：逻辑回归首先计算输入特征的线性组合，即 z=w1x1+w2x2+...+wnxn+b，其中 w 是权重，b 是偏置项，x 是特征值。Sigmoid函数。
复制链接

扫一扫