不同泽尼克多项式的区别和应用（Zernike polynomials and their applications）

1. Zernike多项式简介

泽尼克多项式是在单位圆盘上形成完全正交集的连续函数序列。它们是以荷兰物理学家Frits Zernike的名字命名的，Frits Zernike是1953年诺贝尔物理学奖的获得者，也是相衬显微镜的发明者。由于大多数光学系统都有圆孔，因此泽尼克多项式在波前分析中很有用，因此在光学中起着重要的作用。Zernike多项式一般可分为两种基本类型，即Zernike圆多项式和Zernike环形多项式，它们分别定义在单位圆盘和环形单位圆盘上。Zernike圆多项式最早由Zernike于1934年作为描述相对比法的二阶旋转不变偏微分方程的特征函数引入[1,2]，由Bhatia和Wolf于1954年根据正交性和不变性的要求导出[3]。Zernike环形多项式最早出现在Perkin-Elmer公司1971年的报告中[4]，Tatian于1976年从透镜设计的角度讨论了环形瞳孔光学系统的像差平衡[5]。马哈詹在1981年系统地研究并明确地给出了它们[4]。

Zernike多项式经过介绍后逐渐引起了人们的兴趣，在光学和图像处理中得到了广泛的应用。1942年，Zernike的博士生Bernard Nijboer将对称光学系统的像差函数展开为一系列Zernike多项式，并给出了点物体在像面上复振幅分布的有效表示[6]。这项工作允许对一般光学系统的衍射积分和点扩展函数(PSF)进行分析评估，并被称为Nijboer-Zernike理论。然而，Nijboer-Zernike理论仅在小像差的情况下有效，并且只能在接近几何焦点的位置产生准确的结果。70年后，Janssen用幂-贝塞尔级数给出了一般表达式，并将Nijboer-Zernike理论推广到大像差光学系统[8]。推广的Nijboer-Zernike理论可以解析地计算由Zernike系数描述的像差光学系统的PSF，加速了聚焦场衍射理论的进一步发展。像差衍射理论的发展完全依赖于解析推导，而基于泽尼克多项式的波前分析则依赖于计算机的使用。20世纪70年代，随着自适应光学的兴起，Noll通过对多项式进行归一化和排序，提出了一组修正的Zernike多项式，用于大气湍流引起的波前像差的统计分析[9]。

与此同时，亚利桑那大学的Loomis在干涉图处理软件FRINGE中引入了Zernike多项式的重排序子集，用于干涉测量中的波前分析[10,11]。该子集称为Zernike Fringe集，仅包含37项，但与经典像差具有良好的对应关系。1980年，蒂格将泽尼克多项式的应用从光学到图像处理，并开创了泽尼克矩，它具有旋转不变性，可以用作模式识别的形状描述符[12]。泽尼克矩从那时起就成为图像分析的一个有价值的形状描述符。进入21世纪后，泽尼克多项式的发展逐渐成熟，为了促进有效的交流，美国国家标准协会(ANSI)[13,14]和国际标准化组织(ISO)[15-17]对几个泽尼克集进行了标准化。

泽尼克多项式的广泛应用源于其独特的数学性质。首先，泽尼克多项式在单位圆上是正交的。正交性使得波前函数的展开系数与项数无关[18]。这也使波前的方便的数学操作，如加法，减法，平移，旋转和缩放。其次，虽然在单位圆盘上也存在其他正交多项式，但泽尼克多项式的独特之处在于它与经典像差(如像散、彗差和球差)有良好的对应关系[19,20]。

这使得波前像差的快速分类和量化成为可能。第三，基于(扩展的)Nijboer-Zernike理论[6,8,21]，可以从波前像差的Zernike展开系数解析计算出系统PSF，因此Zernike多项式使得光学系统像质量的评估变得容易。此外，在斜率敏感波前传感器中，Zernike多项式可以作为波前重建的基集，如Shack-Hartmann波前斜率传感器[22,23]和侧向剪切干涉仪[24]，它们是眼科光学和自适应光学中重要的波前传感工具。

如今，世界各地的作者和权威都在使用各种泽尼克多项式的索引。著名的包括Noll索引[9,25]、OSA/ANSI索引[13 - 15,17,26,27]、Fringe/亚利桑那大学索引[10,19]、ISO 14999索引[16,28]、Born和Wolf索引[29]和Malacara索引[30,31]。每一种索引方案采用不同的命名、规范化和索引策略，甚至坐标系统也可能不同，这给使用多项式的研究人员带来了很大的困惑，阻碍了有效的交流。此外，过去几十年发展起来的泽尼克多项式的数学性质，如导数、傅里叶变换和递归关系，在文献中是分散的，没有工作总结这些结果。这促使我们准备了一篇关于泽尼克多项式的综述论文，目的是澄清不同指标的混淆，总结数学性质，调查最先进的应用，并为这个社区的科学家和工程师提供快速参考指南。

 

泽尼克多项式历史上的关键事件

Zernike多项式的索引方式及其应用主题，如下图所示：

 

Zernike多项式的索引方式及其应用主题

本文首字母缩略词和符号列表，如下所示：

 

首字母缩略词和符号列表

 

2. Zernike多项式的不同索引方式

以下为不同索引方式的Zernike多项式：

2.1 Noll Zernike polynomials（Zemax里的Zernike standard polynomials）[25,36]：

 

Noll索引方式的前37项标准正交泽尼克圆多项式

 

 

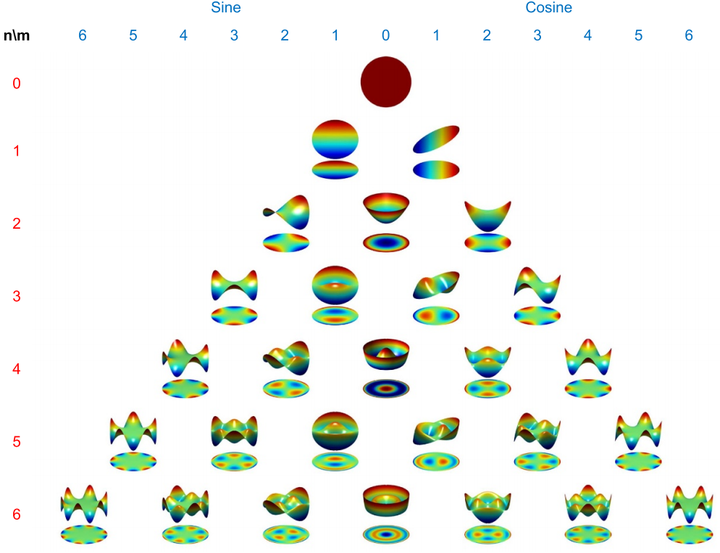
在Noll索引方式下非归一化Zernike圆多项式的前六阶

 

2.2 OSA/ANSI Zernike polynomials（COMSOL射线光学模块）[14,27,39]

 

OSA/ANSI索引下的前37项Zernike多项式

 

2.3 Fringe Zernike polynomials（Zemax、CODE V、OSLO、MetroPro里的Zernike fringe polynomials）[19,25,29]

 

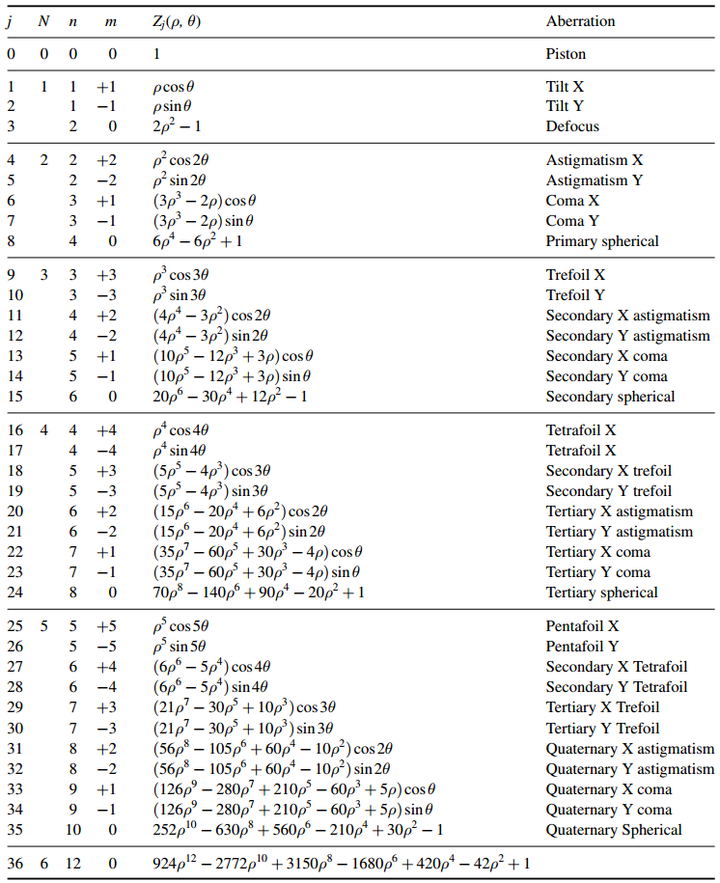
Zernike圆多项式的Fringe索引集

 

2.4 ISO-14999 Zernike polynomials（CODE V里的Extended fringe Zernike polynomials）[16,28]

 

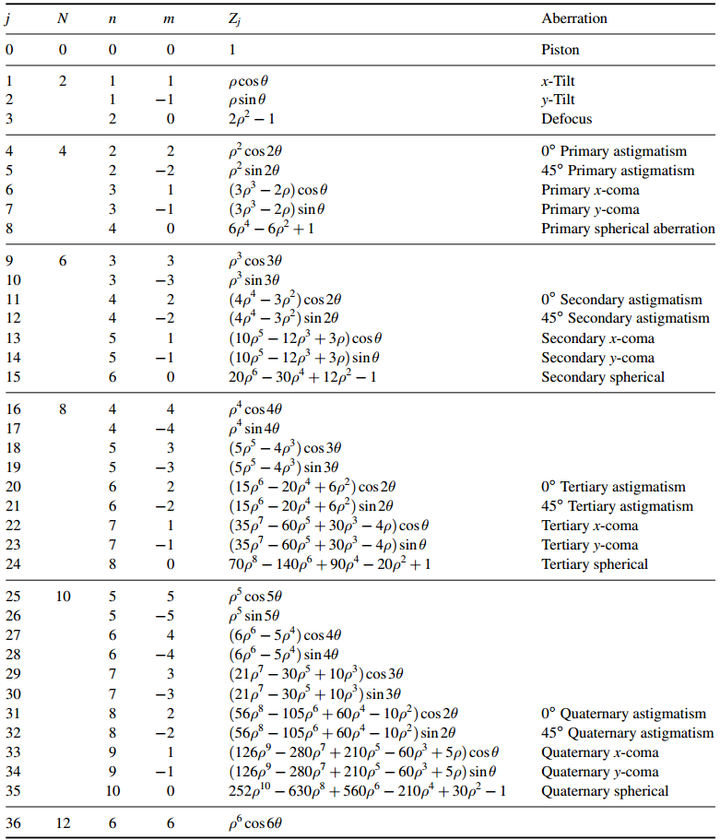
ISO-14999索引下的前37项Zernike圆多项式

 

2.5 Born and Wolf Zernike polynomials（CODE V里的Standard Zernike polynomials）[29]

 

Born和Wolf索引下的前37项Zernike圆多项式

 

2.6 Malacara Zernike polynomials（Malacara索引方式）[31]

 

Malacara指标下的前37项Zernike圆多项式

 

3. 总结

下表从坐标系、归一化和排序策略三方面对Zernike圆多项式的不同标度方案进行了比较和总结，可以看到不同光学设计软件中所使用的Zernike polynomials及其索引方式：

 

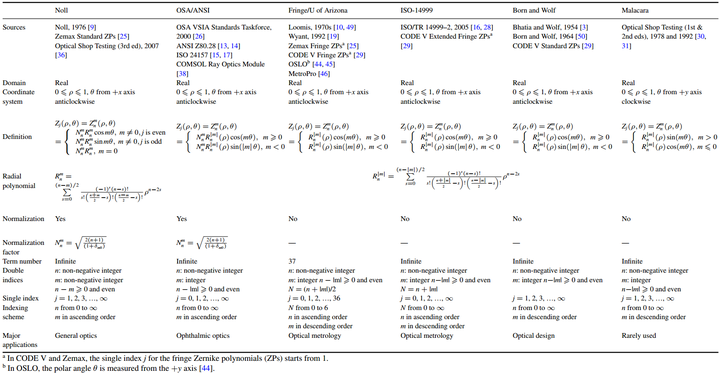
实域上泽尼克圆多项式不同指标的比较

 

特别地，多项式在不同指标下的排序如图所示为前几阶。

 

不同索引的低阶序列的比较

 

下图展示了这六种索引的参考文献来源和应用：

 

不同索引方式及其参考文献总结（ZPs表示泽尼克多项式）

 

参考文献：

[1] Zernike F 1934 Mon. Not. R. Astron. Soc. 94 377–84

[2] Zernike F 1934 Physica 1 689–704

[3] Bhatia A B and Wolf E 1954 Math. Proc. Camb. Phil. Soc. 50 40–48

[4] Mahajan V N 1981 J. Opt. Soc. Am. 71 75–85

[5] Tatian B 1974 J. Opt. Soc. Am. 64 1083–91

[6] Nijboer B R A 1942 PhD Thesis University of Groningen

[7] Mir M, Bhaduri B, Wang R, Zhu R and Popescu G 2012 Quantitative Phase Imaging (Amsterdam: Elsevier) ch 3

[8] Janssen A J E M 2002 J. Opt. Soc. Am. A 19 849–57

[9] Noll R J 1976 J. Opt. Soc. Am. 66 207–11

[10] Loomis J S 1976 FRINGE User’s manual, Version 2 (Tucson: Optical Sciences Center, University of Arizona)

[11] Loomis J 1978 A Computer Program for Analysis of Interferometric Data (Philadelphia: American Society for Testing and Materials)

[12] Teague M R 1980 J. Opt. Soc. Am. 70 920–30

[13] ANSI Z80.28–2004 2004 Ophthalmics—methods of reporting optical aberrations of eyes

[14] ANSI Z80.28–2017 2017 Ophthalmics—methods of reporting optical aberrations of eyes

[15] ISO 24157:2008(E) 2008 Ophthalmic optics and instruments—reporting aberrations of the human eye

[16] International Organization for Standardization (ISO) 2019 ISO/TR 14999–2:2019(E) Optics and photonics—interferometric measurement of optical elements and optical systems—Part 2: measurement and evaluation techniques

[17] ISO 24157:2008/Amd 1:2020 2020 Ophthalmic optics and instruments—reporting aberrations of the human eye

[18] Dai G M 2008 Wavefront Optics for Vision Correction (Bellingham, WA: SPIE Optical Engineering Press)

[19] Wyant J C and Creath K 1992 Basic Wavefront Aberration Theory for Optical Metrology (New York: Academic)

[20] Alonso J, Gómez-Pedrero J A and Quiroga J A 2019 Modern Ophthalmic Optics (Cambridge: Cambridge University Press)

[21] Nijboer B R A 1947 Physica 13 605–20

[22] Southwell W H 1980 J. Opt. Soc. Am. 70 998–1006

[23] Liang J, Grimm B, Goelz S and Bille J F 1994 J. Opt. Soc. Am. A 11 1949–57

[24] Dai F, Tang F, Wang X, Sasaki O and Feng P 2012 Appl. Opt. 51 5028–37

[25] Zemax 2018 Zemax OpticStudio 18.4 User Manual pp 990–1000

[26] Thibos L N, Applegate R A, Schwiegerling J T and Webb R 2000 OSA Vision Science and Its Applications (Santa Fe, New Mexico, United States) (Standards for Reporting the Optical Aberrations of Eyes)

[27] Thibos L N, Applegate R A, Schwiegerling J T and Webb R 2002 J. Refract. Surg. 18 652–60

[28] International Organization for Standardization (ISO) 2005 Optics and photonics—interferometric measurement of optical elements and optical systems—Part 2: measurement and evaluation techniques

[29] Synopsys Inc 2017 CODE V V11.1 Reference Manual: Appendix A Zernike Polynomials

[30] Malacara-Hernández D 1978 Appendix II. Zernike Polynomials and Wavefront Fitting (Hoboken, NJ: Wiley)

[31] Malacara-Hernández D and DeVore S L 1992 Interferogram Evaluation and Wavefront Fitting (Hoboken, NJ: Wiley) ch 13

[32] Born M and Wolf E 1999 Principles of Optics (Cambridge: Cambridge University Press)

[33] Lakshminarayanan V and Fleck A 2011 J. Mod. Opt. 58 545–61

[34] Wang J Y and Silva D E 1980 Appl. Opt. 19 1510–8

[35] Mahajan V N 1994 Appl. Opt. 33 8121–4

[36] Mahajan V N 2007 Zernike Polynomials and Wavefront Fitting (Hoboken, NJ: Wiley) ch 13

[37] Mahajan V N and Dai G M 2007 J. Opt. Soc. Am. A 24 2994–3016

[38] COMSOL 2018 Ray optics module User’s guide pp 156–8

[39] Sinjab M M and Cummings A B 2018 Introduction to Wavefront Science (Berlin: Springer) ch 2

---

本文引自：K. Niu and C. Tian*, "Zernike polynomials and their applications," Journal of Optics 24, 123001 (2022)

（本文为CSDN“光学码农”原创，转载须注明本文网址，违者必究！）