基于双层优化的微电网系统规划容量配置方法，规划出最佳的微电网光伏、风电、储能等多电源的容量配置方案

基于双层优化的微电网系统规划容量配置方法
摘要：与目前大部分的微网优化调度代码不同，本代码主要做的是微网的多电源容量优化配置，规划出最佳的微电网光伏、风电、储能等多电源的容量配置方案，此外，代码采用双层模型，上层以周期内运维成本以及投资成本之和最低为目标函数，下层则以调度周期内购售电成本以及燃料成本最低为目标函数，上层得出最佳容量配置方案，下层得出最佳运行策略。
出图效果也非常清楚，具体可以看下图。

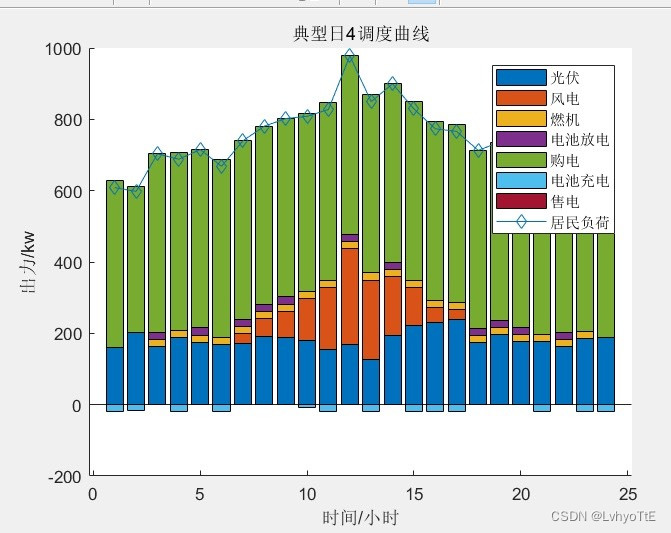
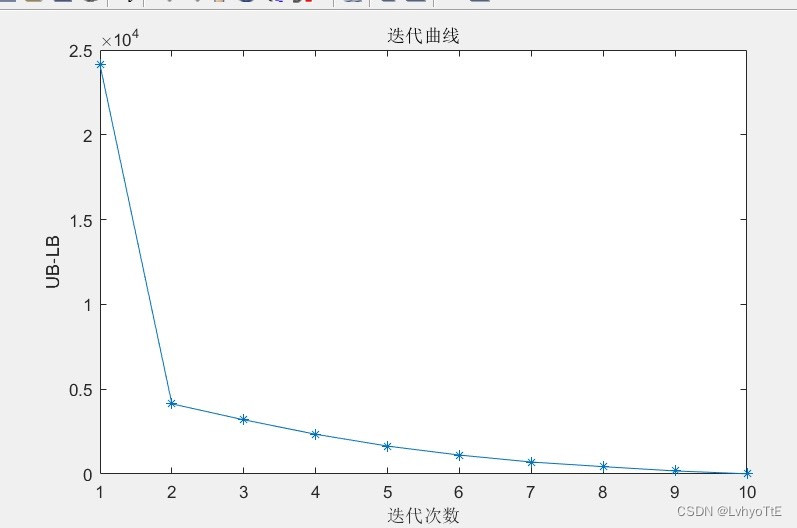
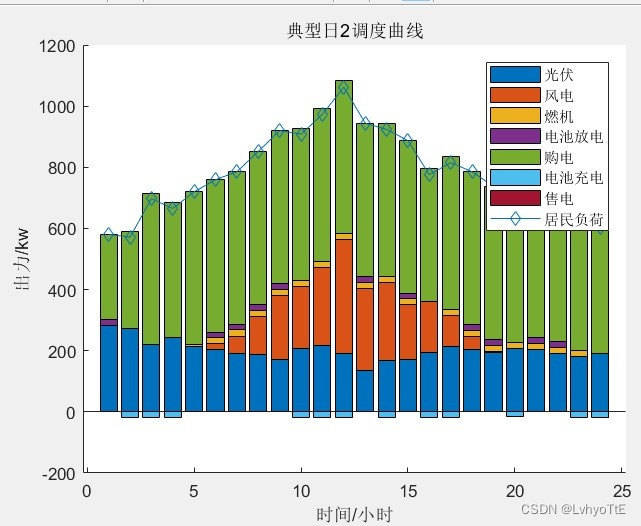
论文题目：基于双层优化的微电网系统规划容量配置方法

摘要： 随着全球对可再生能源的需求不断增加，微电网系统在现代电力系统中变得越来越重要。然而，微电网系统在不同的时间段内需要不同的电源来保证其稳定性和可靠性。因此，如何进行微电网系统规划容量配置是至关重要的问题。本文提出了一种基于双层优化的微电网系统规划容量配置方法，该方法能够有效地解决微电网系统的规划问题，并优化系统的成本。

首先，本文提出了基于双层模型的微电网系统规划容量配置方法。上层模型采用周期内运维成本和投资成本之和最小化作为目标函数，并通过混合整数线性规划来求解最优容量。下层模型以调度周期内购售电成本以及燃料成本最低为目标函数，将最佳容量配置方案转化为最佳运行策略。

其次，本文介绍了基于双层优化的微电网系统规划容量配置算法的具体实现过程。该算法包括两个主要步骤：上层容量配置和下层运行调度。在上层容量配置阶段，使用混合整数线性规划算法来优化问题求解，确定最优的电源容量配置方案。在下层运行调度阶段，通过线性规划和整数规划算法来计算最佳运行策略。

最后，通过实际的案例分析和仿真验证，本文证实了该方法的高效性和可行性。基于双层优化的微电网系统规划容量配置方法能够对微电网系统进行高效的规划和容量配置，从而优化系统的成本，并提高其稳定性和可靠性。

关键词：微电网系统，容量配置，双层优化，线性规划，整数规划，混合整数线性规划

引言： 微电网是一种能够自主发电和自主消费的小型电网系统，其具有较高的稳定性、可靠性和可持续性。微电网系统通常由多种电源组成，包括发电机、光伏电池、风力发电机、储能设备等。为了保证微电网系统的稳定性和可靠性，需要对其进行规划容量配置。在规划容量配置过程中，需要考虑多种因素，包括能源供应和需求的特点、电池性能、传输线路的布局和容量等。因此，如何进行微电网系统规划容量配置是至关重要的问题。

相关工作： 近年来，微电网系统的规划容量配置问题已得到广泛关注。目前，研究人员主要关注以下几个方面：

1. 基于贪心算法的容量配置方法。这种方法通常只考虑单一目标，如最小化系统成本等。然而，这种方法的优化能力不足，容易陷入局部最优解。
2. 基于粒子群算法和遗传算法的容量配置方法。这种方法可以考虑多个目标，但其计算复杂度较高，且结果的优化效果不稳定。
3. 基于混合整数线性规划的容量配置方法。该方法可以有效地求解微电网系统规划容量配置问题，并能够考虑多个目标。然而，该方法计算复杂度较高，需要高级算法的支持。

方法： 本文提出了一种基于双层优化的微电网系统规划容量配置方法。该方法采用双层模型，在上层以周期内运维成本以及投资成本之和最低为目标函数，下层则以调度周期内购售电成本以及燃料成本最低为目标函数。上层得出最佳容量配置方案，下层得出最佳运行策略。

具体地，该方法包括两个主要步骤：上层容量配置和下层运行调度。在上层容量配置阶段，使用混合整数线性规划算法来优化问题求解。在下层运行调度阶段，通过线性规划和整数规划算法来计算最佳运行策略。具体的算法流程如下：

1. 上层容量配置 在该阶段，我们需要根据能源供应和需求的特点来确定最优的电源容量配置方案，使得运维成本和投资成本之和最小化。具体地，我们可以采用混合整数线性规划算法来求解该问题，假设有n种电源，分别为i = 1, 2, …, n。则该问题的目标函数可以表示为：

minimize Z1 = ∑Ci * Xi + ∑Di * Yi

其中，Ci表示电源i的固定成本，Xi为表示电源i的容量变量，Yi表示电源i是否安装的二进制变量，Di表示电源i的可变成本。

目标函数的约束条件如下：

1. 能源供应和需求的平衡： ∑Pi = ∑Di + ∑Si

其中，Pi表示电源i的产出，Di表示电源i的需求，Si表示电网的供给。

1. 容量约束：

Ximin ≤ Xi ≤ Ximax * Yi

其中，Ximin和Ximax分别表示电源i的最小和最大容量，Yi表示是否安装电源i。

1. 布局约束： ∑Yi ≤ M

其中，M表示可以安装的电源数量上限。该约束条件保证了系统的可行性。

1. 下层运行调度 在该阶段，我们需要根据最优容量配置方案制定最佳的运行策略。具体地，我们采用线性规划和整数规划算法来计算最佳运行策略。假设有m个时间段，分别为t = 1, 2, …, m，系统中有n种电源，分别为i = 1, 2, …, n，则该问题的目标函数可以表示为：

minimize Z2 = ∑ αit * Pit + ∑ βit * Vit + ∑ γit * Fit

其中，Pit表示电源i在时间段t的产出，Vit表示电源i在时间段t的购电量，Fit表示电源i在时间段t的燃料成本，αit表示购电量的单价，βit表示电源i的销售价，γit表示电源i的燃料单价。

目标函数的约束条件如下：

1. 供需平衡： ∑Pi ≥ ∑Di + Si

其中，Pi表示电源i的产出，Di表示电源i的需求，Si表示电网的供给。

1. 容量限制： Pimin ≤ Pit ≤ Pimax

其中，Pimin和Pimax分别表示电源i在时间段t的最小和最大产出。

1. 费用约束： ∑ (αit * Vit - βit * Pit - γit * Fit) ≤ 0

以上约束条件保证了系统的可行性，并通过线性规划和整数

相关代码,程序地址：http://lanzouw.top/687682785629.html