结构动力学~试验用悬臂梁的动特性及基于模态叠加法的响应分析

Lzh_023016

已于 2023-12-30 22:44:07 修改

阅读量2.4k

点赞数 31

分类专栏： Matlab 有限元文章标签： matlab 算法

于 2023-12-30 22:42:57 首次发布

本文链接：https://blog.csdn.net/Lzh_023016/article/details/135310674

版权

Matlab 同时被 2 个专栏收录

20 篇文章 2 订阅

订阅专栏

有限元

3 篇文章 0 订阅

订阅专栏

一、实验任务

以第一个试验用的悬臂梁为例，用有限元法编程生成质量矩阵和刚度矩阵（采用平面梁单元，单元数在10到30之间）。
使用matlab的用于广义特征值问题分析的函数（eig(A,B,‘chol’)，该命令使用乔莱斯基分解的方法，计算对称矩阵A和对称正定矩阵B的广义特征值问题。A对应刚度矩阵，B对应质量矩阵）计算梁的前三阶固有频率和振型，计算得到梁的前三阶固有频率和振型，并画出振型图，与试验的频率和振型值进行对比，分析造成误差的可能原因。
假设改梁在端部横向向下作用一个正弦激励力（自行给定力的幅值和频率，其中频率设定为系统第一阶和第二阶固有频率和的一半），用模态叠加法计算激励位置上的稳态响应，画出稳态响应曲线。其中阻尼矩阵的构造采用比例阻尼，前两阶阻尼比均设为0.008。同时采用模态加速度方法计算该处响应幅值，与模态位移法进行比较，分析当分别保留一阶模态，二阶模态，三阶模态时对响应幅值计算的影响。

二、理论分析

（1）力学模型
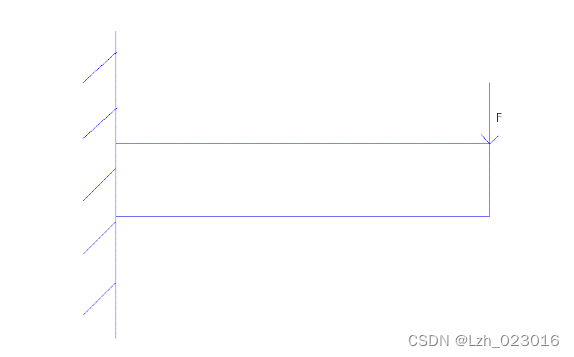
在这里插入图片描述
（2）计算梁的前三阶固有频率和振型，计算得到梁的前三阶固有频率和振型。
首先，用有限元的方法将悬臂梁分成20等份，计算每个梁单元的质量矩阵和刚度矩阵

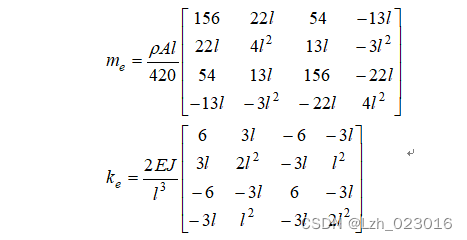
再将单元矩阵组装成悬臂梁的刚度矩阵K和质量矩阵M。
然后通过cholesky分解，应用MATLAB eig(K,M,’chol’)命令求解悬臂梁的前40阶固有频率，并得到各阶模态矩阵。
这里要注意，模态矩阵为40乘1的矩阵，它奇数行元素代表挠度，偶数行元素代表转角，所以应当单独将奇数行挑出来画振型图。
（3）模态叠加法计算激励位置上的稳态响应，画出稳态响应曲线
在这里插入图片描述
（4）模态加速度方法计算该处响应幅值，与模态位移法进行比较，分析当分别保留一阶模态，二阶模态，三阶模态时对响应幅值计算的影响

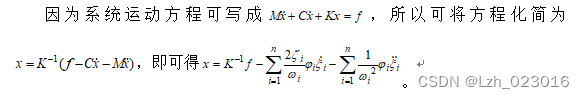
三、源代码

L = 3; %实验测得悬臂梁长度
T = 0.15; %实验测得悬臂梁厚度
B = 0.2; %实验测得悬臂梁宽度
E = 3.2e10; %悬臂梁弹性模量
u = 0.28; %悬臂梁泊松比
p = 2.5e3; %悬臂梁密度
n = 10; %将悬臂梁生成20个平面梁单元
le = L/n;
A = B*T;
J = B*T^3/12;
%单元质量矩阵
me = [156 22*le 54 -13*le;22*le 4*le*le 13*le -3*le*le;54 13*le 156 -22*le;-13*le -3*le*le -22*le 4*le*le]*p*A*le/420;
%单元刚度矩阵
ke = [6 3*le -6 3*le;3*le 2*le*le -3*le le*le;-6 -3*le 6 -3*le;3*le le*le -3*le 2*le*le]*2*E*J/le^3;
K = zeros(2*n,2*n); %悬臂梁刚度矩阵
M = zeros(2*n,2*n); %悬臂梁质量矩阵
%接下来组装刚度矩阵和质量矩阵
K(1,1) = ke(3,3);
K(1,2) = ke(3,4);
K(2,1) = ke(4,3);
K(2,2) = ke(4,4);
M(1,1) = me(3,3);
M(1,2) = me(3,4);
M(2,1) = me(4,3);
M(2,2) = me(4,4);
i = 1;
while (i <= n-1)
    M(2*i-1,2*i-1) = M(2*i-1,2*i-1)+me(1,1);
    M(2*i-1,2*i) = M(2*i-1,2*i)+me(1,2);
    M(2*i-1,2*i+1) = M(2*i-1,2*i+1)+me(1,3);
    M(2*i-1,2*i+2) = M(2*i-1,2*i+2)+me(1,4);
    M(2*i,2*i-1) = M(2*i,2*i-1)+me(2,1);
    M(2*i,2*i) = M(2*i,2*i)+me(2,2);
    M(2*i,2*i+1) = M(2*i,2*i+1)+me(2,3);
    M(2*i,2*i+2) = M(2*i,2*i+2)+me(2,4);
    M(2*i+1,2*i-1) = M(2*i+1,2*i-1)+me(3,1);
    M(2*i+1,2*i) = M(2*i+1,2*i)+me(3,2);
    M(2*i+1,2*i+1) = M(2*i+1,2*i+1)+me(3,3);
    M(2*i+1,2*i+2) = M(2*i+1,2*i+2)+me(3,4);
    M(2*i+2,2*i-1) = M(2*i+2,2*i-1)+me(4,1);
    M(2*i+2,2*i) = M(2*i+2,2*i)+me(4,2);
    M(2*i+2,2*i+1) = M(2*i+2,2*i+1)+me(4,3);
    M(2*i+2,2*i+2) = M(2*i+2,2*i+2)+me(4,4);
    
    K(2*i-1,2*i-1) =K(2*i-1,2*i-1)+ ke(1,1);
    K(2*i-1,2*i) =  K(2*i-1,2*i)+ke(1,2);
    K(2*i-1,2*i+1) =  K(2*i-1,2*i+1)+ke(1,3);
    K(2*i-1,2*i+2) = K(2*i-1,2*i+2)+ke(1,4);
    K(2*i,2*i-1) = K(2*i,2*i-1)+ke(2,1);
    K(2*i,2*i) = K(2*i,2*i)+ke(2,2);
    K(2*i,2*i+1) =  K(2*i,2*i+1)+ke(2,3);
    K(2*i,2*i+2) = K(2*i,2*i+2)+ke(2,4);
    K(2*i+1,2*i-1) = K(2*i+1,2*i-1)+ke(3,1);
    K(2*i+1,2*i) = K(2*i+1,2*i)+ke(3,2);
    K(2*i+1,2*i+1) = K(2*i+1,2*i+1)+ke(3,3);
    K(2*i+1,2*i+2) = K(2*i+1,2*i+2)+ke(3,4);
    K(2*i+2,2*i-1) = K(2*i+2,2*i-1)+ke(4,1);
    K(2*i+2,2*i) =  K(2*i+2,2*i)+ke(4,2);
    K(2*i+2,2*i+1) =  K(2*i+2,2*i+1)+ke(4,3);
    K(2*i+2,2*i+2) = K(2*i+2,2*i+2)+ke(4,4);
    i = i+1;
end
%使用乔莱斯基分解法求固有频率和模态矩阵
[x1,x2] = eig(K,M,'chol');
omega = sqrt(diag(x2));%固有频率
fprintf('第一阶固有频率= %g\n',omega(1));
fprintf('第二阶固有频率= %g\n',omega(2));
fprintf('第三阶固有频率= %g\n',omega(3));
x =1:1:20;
y1 = x1(:,1);
y2 = x1(:,2);
y3 = x1(:,3);
fai1 = zeros(20,1);
fai2 = zeros(20,1);
fai3 = zeros(20,1);
i = 1;
while (i<=20)
    fai1(i) = y1(2*i-1);
    fai2(i) = y2(2*i-1);
    fai3(i) = y3(2*i-1);
    i = i+1;
end
%画一阶振型图
figure(1)
plot(x,fai1,'linewidth',1);
hold on;
grid on;
title('第一阶振型图');
xlabel('x');
ylabel('幅值');
%画二阶振型图
figure(2)
plot(x,fai2,'linewidth',1);
hold on;
grid on;
title('第二阶振型图');
xlabel('x');
ylabel('幅值');
%画三阶振型图
figure(3)
plot(x,fai3,'linewidth',1);
hold on;
grid on;
title('第三阶振型图');
xlabel('x');
ylabel('幅值');
%画出实验测得悬臂梁前两阶振型图
x=1:1:5;
faice1=[18.426;17.2;6.246;4.429;1.124];
faice2=[-10.651;1.018;9.486;13.112;5.116];
figure(4)
plot(x,faice1,'linewidth',1);
hold on;
grid on;
title('实验测得第一阶振型图');
xlabel('x');
ylabel('幅值');
figure(5)
plot(x,faice2,'linewidth',1);
hold on;
grid on;
title('实验测得第二阶振型图');
xlabel('x');
ylabel('幅值');

%求外激励作用在端部，端部的稳态响应曲线
%先求出阻尼矩阵
zb = 0.008;
w1 = omega(1);
w2 = omega(2);
a0 = 2*w1*w2*zb/(w1+w2);
a1 = 2*zb/(w1+w2);
C = a0*M + a1*K;
%再进行归一化处理
m = x1'*M*x1; c  = x1'*C*x1; k = x1'*K*x1;
w = (omega(1)+omega(2))/2; %外激励的频率
A = 10000; %外激励的幅值
H39 = 0; H40 = 0;
a = 1;
while(a<=40)
    H39 = H39+x1(39,a)*x1(39,a)/(k(a,a)-m(a,a)*w^2+1i*w*c(a,a));
    H40 = H40+x1(40,a)*x1(39,a)/(k(a,a)-m(a,a)*w^2+1i*w*c(a,a));
    a = a+1;
end
t = 0:0.001:0.2;
X39 = abs(H39).*A.*sin(w*t);
A39 = abs(H39)*A;
X40 = abs(H40).*A.*sin(w*t);
A40 = abs(H40)*A;
fprintf('模态叠加法计算的端部横向位移稳态响应的幅值大小= %g\n',A39);
fprintf('模态叠加法计算的端部转角稳态响应的幅值大小= %g\n',A40);
figure(6)
plot(t,X39,'linewidth',1);
hold on;
grid on;
title('端部横向位移的稳态响应曲线');
xlabel('t');
ylabel('挠度');
figure(7)
plot(t,X40,'linewidth',1);
hold on;
grid on;
title('端部转角的稳态响应曲线');
xlabel('t');
ylabel('转角');

%用模态加速度法计算端部稳态响应的幅值，并用模态截断法与模态位移法进行比较，
%分析当分别保留一阶模态，二阶模态，三阶模态时对响应幅值计算的影响
a = 1;
k0 = K^(-1);
xishu1 =0; xishu2 =0;xishu3 =0; xishu4 =0;
while (a <=40)
    zb = c(a,a)/(2*m(a,a)*omega(a));
    xishu1 = xishu1-2*w*zb*x1(39,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a));
    xishu2 = xishu2+w*w*x1(39,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a)*omega(a));
    xishu3 = xishu3-2*w*zb*x1(40,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a));
    xishu4 = xishu4+w*w*x1(40,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a)*omega(a));
    a = a+1;
end
AA39 = k0(39,39)+xishu2-1i*xishu1;
AA39 = A*abs(AA39);
AA40 = k0(39,40)+xishu4-1i*xishu3;
AA40 = A*abs(AA40);
fprintf('模态加速度法计算的端部横向位移稳态响应的幅值大小= %g\n',AA39);
fprintf('模态加速度法计算的端部转角稳态响应的幅值大小= %g\n',AA40);

%分别保留一阶模态，二阶模态，三节模态模态叠加法和模态加速度法计算的响应幅值
a = 1;xishu1 =0; xishu2 =0;xishu3 =0; xishu4 =0;H39 = 0; H40 = 0;
while (a <=3 )
    fprintf('n= %g\n',a);
    zb = c(a,a)/(2*m(a,a)*omega(a));
    xishu1 = xishu1-2*w*zb*x1(39,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a));
    xishu2 = xishu2+w*w*x1(39,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a)*omega(a));
    xishu3 = xishu3-2*w*zb*x1(40,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a));
    xishu4 = xishu4+w*w*x1(40,a)*x1(39,a)/((k(a,a)-m(a,a)*w^2+1i*w*c(a,a))*omega(a)*omega(a));
    AA39 = k0(39,39)+xishu2-1i*xishu1;
    AA39 = A*abs(AA39);
    AA40 = k0(39,40)+xishu4-1i*xishu3;
    AA40 = A*abs(AA40);
    H39 = H39+x1(39,a)*x1(39,a)/(k(a,a)-m(a,a)*w^2+1i*w*c(a,a));
    H40 = H40+x1(40,a)*x1(39,a)/(k(a,a)-m(a,a)*w^2+1i*w*c(a,a));
    A39 = abs(H39)*A;
    A40 = abs(H40)*A;
    fprintf('模态加速度法计算的端部横向位移稳态响应的幅值大小= %g\n',AA39);
    fprintf('模态叠加法计算的端部横向位移稳态响应的幅值大小= %g\n',A39);
    fprintf('模态加速度法计算的端部转角稳态响应的幅值大小= %g\n',AA40);
    fprintf('模态叠加法计算的端部转角稳态响应的幅值大小= %g\n',A40);
    a = a+1;
end

四、结果

（1）梁的前三阶固有频率和振型，并画出振型图
理论值：
第一阶固有频率= 117.726
第二阶固有频率= 737.777
第三阶固有频率= 2065.83
实验值：
第一阶固有频率= 105.793
第二阶固有频率= 683.810
A、理论第一阶振型图
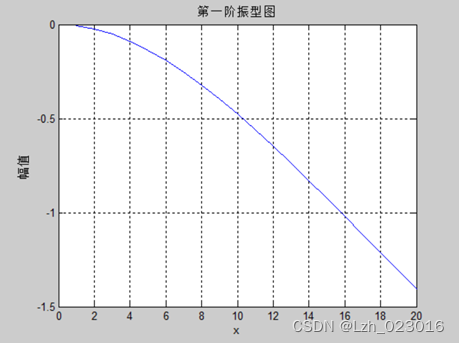
在这里插入图片描述
B、理论第二阶振型图

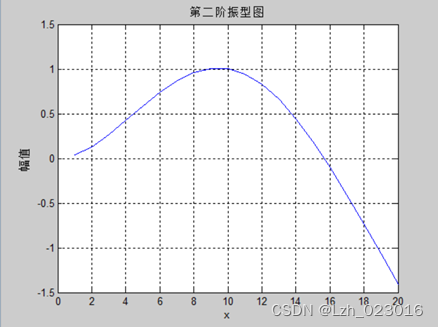
C、理论第三阶振型图

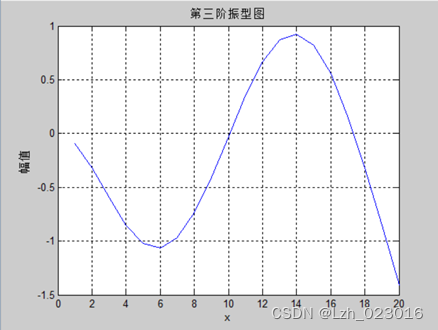
D、实验测得第一阶振型图

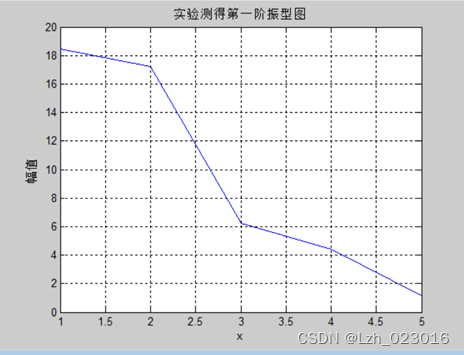
E、实验测得第二阶振型图

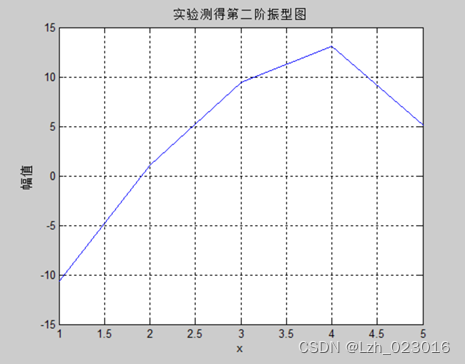
（2）模态叠加法计算激励位置上的稳态响应，画出稳态响应曲线
模态叠加法计算的端部横向位移稳态响应的幅值大小= 0.0552161；
模态叠加法计算的端部转角稳态响应的幅值大小= 0.285662；
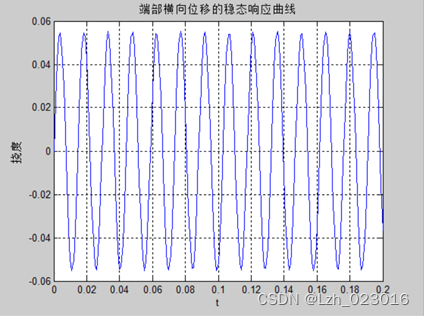
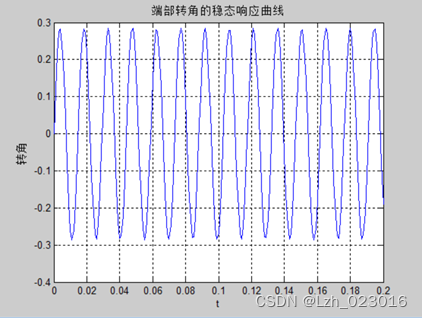
在这里插入图片描述

（3）态加速度方法计算该处响应幅值，与模态位移法进行比较，分析当分别保留一阶模态，二阶模态，三阶模态时对响应幅值计算的影响。
模态加速度法计算的端部横向位移稳态响应的幅值大小= 0.0568295
模态加速度法计算的端部转角稳态响应的幅值大小= 0.287375

n= 1
模态加速度法计算的端部横向位移稳态响应的幅值大小= 0.0750741
模态叠加法计算的端部横向位移稳态响应的幅值大小= 0.116852
模态加速度法计算的端部转角稳态响应的幅值大小= 0.138581
模态叠加法计算的端部转角稳态响应的幅值大小= 0.271015

n= 2
模态加速度法计算的端部横向位移稳态响应的幅值大小= 0.0570599
模态叠加法计算的端部横向位移稳态响应的幅值大小= 0.0621865
模态加速度法计算的端部转角稳态响应的幅值大小= 0.284427
模态叠加法计算的端部转角稳态响应的幅值大小= 0.169596

n= 3
模态加速度法计算的端部横向位移稳态响应的幅值大小= 0.0568492
模态叠加法计算的端部横向位移稳态响应的幅值大小= 0.0573507
模态加速度法计算的端部转角稳态响应的幅值大小= 0.287105
模态叠加法计算的端部转角稳态响应的幅值大小= 0.233547

五、结论

（1）实验测得悬臂梁的第一阶固有频率为105.793，第二阶固有频率为683.810，理论计算得悬臂梁的第一阶固有频率为117.726，第二阶固有频率为737.777（此处使用的是角频率）。所以，实验测得悬臂梁第一阶固有频率的误差为10.136％，第二阶固有频率的误差为7.315％。误差产生的原因可能有：一、本实验采用了一致协调矩阵的方法，计算得到的固有频率偏大。二、测量悬臂梁时，没有把悬臂梁内部的长度测量进去，使悬臂梁长度的测量值偏小，从而理论计算得到的固有频率偏大；
（2）实验测得的前两阶振型图与理论计算得到的振型图在一定误差范围内一直，说明理论计算得到的模态矩阵比较可靠；
（3）模态加速度法和模态叠加法计算得到端部的稳态响应幅值在误差范围内可近似相等；
（4）由模态截断可知，模态加速度法收敛速度明显比模态叠加法快，这是因为分别在分母出现，所以高阶模态对响应的贡献就越来越小，这样就加快了收敛速度，基本n取到3就可以收敛了。

Lzh_023016

关注

31
点赞
踩
39

收藏

觉得还不错? 一键收藏
0
评论
结构动力学~试验用悬臂梁的动特性及基于模态叠加法的响应分析

以第一个试验用的悬臂梁为例，用有限元法编程生成质量矩阵和刚度矩阵（采用平面梁单元，单元数在10到30之间）。使用matlab的用于广义特征值问题分析的函数（eig(A,B,‘chol’)，该命令使用乔莱斯基分解的方法，计算对称矩阵A和对称正定矩阵B的广义特征值问题。A对应刚度矩阵，B对应质量矩阵）计算梁的前三阶固有频率和振型，计算得到梁的前三阶固有频率和振型，并画出振型图，与试验的频率和振型值进行对比，分析造成误差的可能原因。
复制链接

扫一扫