论文笔记之Stein变分梯度下降

论文地址：点这里。作者还提供了Stein变分梯度下降法的源码。
Note：
源码不涉及深度学习，所以PyTorch用户或者TF用户都可以使用。

Stein变分梯度下降(SVGD)可以理解是一种和随机梯度下降(SGD)一样的优化算法。在强化学习算法中，Soft-Q-Learning使用了SVGD去优化，而Soft-AC选择了SGD去做优化。

Abstract

本文旨在提供一种新的变分推断(VI)算法用来做梯度下降(优化)。通过优化两个分布的KL散度，粒子不断迭代，使之从初始的分布一步步达到目标分布。算法涉及到Stein特征的平滑转换以及核差异(KSD)。
Note：

1. 关于KSD的介绍，可以参考我的另一篇论文笔记。

1 Introduction

贝叶斯推断是一种模型估计的方法，核心就是那个贝叶斯公式。该公式中有一个归一化因子$p(x)=\int p(x)\mathrm{d}x$，当高维问题时候，计算将变得困难。因此MCMC和VI这两种方法就应运而生，用于解决这个计算复杂度问题。
马尔科夫链蒙特卡洛(MCMC)的缺陷在于收敛慢且难收敛，优点是偏差较小，毕竟是个需要采样的方法(强化学习最初的MC方法也有这2个特点)。
变分推断(VI)是一种优化算法，用随机梯度下降最小化目标分布与估计分布之间的KL散度，其优点是优化速度快适合于大数据，缺陷是存在较大的偏差，优化结果的好坏与否取决于最先定义的数簇(如经典的平均场变分数簇)偏差大小。
最大后验概率(MAP)是一种依靠先验知识的计算后验概率的方法，这是一种MAP贝叶斯，并不是全贝叶斯。
作者提出一种新型通用的变分推断算法——Stein变分梯度下降。可以看成是一种用于贝叶斯推断的梯度下降方法。它有以下特点：

1. 使用粒子去做分布的估计。
2. 是一种梯度下降算法，可以用在任何使用SGD做优化的地方。
3. 是一种最小化目标分布和估计分布间KL散度的算法，不断地驱动粒子去拟合(fit)目标分布。
4. 算法引入了平滑转换、KSD(Stein方法+RKHS)。
5. 是一种全贝叶斯算法。
6. 当使用单个粒子的时候，该算法就相当于对MAP做梯度下降；当使用所有的粒子的时候，就是全贝叶斯算法。
7. 是一种超越经典VI的新VI算法。
8. Stein梯度下降最大的贡献在于：它在再生核希尔伯特空间下给出了使得KL散度下降最快的确定性方向。

2 Background

这里是对贝叶斯中的后验分布$p(x)=\bar{p}(x)/Z$以及KSD的介绍。KSD有个优点在于通过使用Stein得分函数${\nabla }_x\log p(x)$来避免计算归一化因子$Z$。

3 Variational Inference Using Smooth Transforms

VI做模型估计：
目标分布$p(x)$，估计分布$q(x)$，数簇 Q = { q ( x ) } \mathcal{Q}=\{q(x)\} Q={q(x)}，通过优化KL散度来得到估计模型$q^{\ast }$：
q ∗ = arg min ⁡ q ∈ Q { K L ( q ∣ ∣ p ) = E q [ log ⁡ q ( x ) ] − E q [ log ⁡ p ˉ ( x ) ] + log ⁡ Z } (4) q^*=\argmin_{q\in\mathcal{Q}}\{KL(q||p)=\mathbb{E}_q[\log q(x)]-\mathbb{E}_q[\log\bar{p}(x)]+\log Z\}\tag{4} q∗=q∈Qargmin​{KL(q∣∣p)=Eq​[logq(x)]−Eq​[logpˉ​(x)]+logZ}(4)
VI就是通过这种方式来免除归一化因子的计算。问题就是这个数簇$\mathcal{Q}$很难去选择一个合适通用的。
作者指出，合适的$\mathcal{Q}$应该具备以下原则：

1. 准确性：广度足够以至于可以近似一系列目标分布。
2. 计算可行性：容易去计算，不要整个难以实现的。
3. 可解决性：可以和KL散度优化结合起来。

在此基础上，作者引入平滑变换$T:\mathcal{X}\to \mathcal{X},\mathcal{X}\subset {\mathbb{R}}^d$，也就是说将$\mathcal{Q}$看成一个一对一平滑变换$z=T(x),x\in \mathcal{X}$得到的数簇，且$x\sim q_0(x)$。
Note：

1. 一对一的原因在于：①必须保证是函数。②如果是多对一的话，就不能保证是增量转换(单调)了，比如如果T是个$y=x^2$，那么当你粒子$x$经过好几轮平滑转化之后，$q$已经发生改变了，这时候你从$q$采样的$x$经过平滑转换可能就会回到之前发生过的某个$q$分布了，这是不允许的，因为这样就有点回环曲折的意思，不能保证最快的优化了。

那么经过$T$之后的数簇是怎么样的呢？利用坐标变换公式可得：
$$q_{[T]}(z)=q(x)\cdot |\det (\frac{\partial x}{\partial z})|=q(T^{-1}(z))\cdot |\det ({\nabla }_z{T}^{-1}(z))|$$其中$\det ({\nabla }_z{T}^{-1}(z))$是矩阵$T^{-1}(z)$的雅克比行列式。
或者反过来：
$$q_{[T^{-1}]}(x)=q(T(x))\cdot |\det ({\nabla }_{x}T(x))|$$作者指出平滑变化的引入使得准确性和计算可行性满足了，可是可解决性还不能满足，因此一种方法是将$T$参数化，但参数化将面临3个问题：

1. 需要选择合适的参数表示来平衡三个原则。
2. 参数化表示不一定能满足T的一对一性。
3. 参数化不一定使得Jacobian可以得到有效计算。

参数化既然这么麻烦，作者索性放弃选用了一种不需要参数化表示$T$的方法——一种迭代式构建增量变化的方法，在RKHS下，可表现出最快的梯度下降方向：

1. 该方法不需要计算雅克比矩阵。
2. 形式上简单，类似于经典的梯度下降算法，可计算性强。

3.1 Stein Operator as the Derivative of KL Divergence

作者提出了转换的表达式：$T(x)=x+ϵ\cdot \varphi (x)$。
Note：

1. 这个表达式长得很像梯度下降吧，意味着$\varphi (x)$代表着方向。
2. $ϵ$是一个很小很小的数。
3. $\varphi (x)$可微，是一个向量。
4. 当$|ϵ|$很小的时候。$T(x)\approx x$，所以其雅可比矩阵${\nabla }_x{T}^{-1}$就是个单位阵，显然雅克比行列式不等于0，根据反函数理论，保证了$T$的单调性，也就保证了一对一。

接下来就是本文最重要的地方之一了。

Lemma1
如果$X\in \mathcal{X},\mathcal{X}\subset \mathbb{R}$，$F$是平滑变换，则：
$$\frac{\partial \det (F(X))}{\partial {F(X)}^T}=\det (F(X))\cdot F^{-1}(X)$$证明如下：

Note:

1. 求导对象$x$必须是方阵。

Lemma2
如果$p(x)、q(x)$都是光滑的函数，$x\in \mathcal{X}$，$T=T_{ϵ}(x)$是个一对一的转换函数，且对$x,ϵ$都可微，$s_p(x)$为Stein得分函数，$q_{[T]}$是$x\sim q$时$z=T_{ϵ}(x)$的概率密度函数，则：
$${\nabla }_{ϵ}KL(q[T]||p)={\mathbb{E}}_q[s_p^T(T(x)){\nabla }_{ϵ}T(x)+tr(({\nabla }_{x}T(x){)}^{-1}\cdot ({\nabla }_{ϵ}{\nabla }_{x}T(x)))]$$证明如下：

Note：

1. 画红色的转置$T$和迹$tr$是为了输出格式的需要。
2. 原论文补充材料中的推导对最后的结果漏了一个转置符$T$。

Theorem 3.1.
$T(x)=x+ϵ\cdot \varphi (x)$，平滑变换$z=T(x)$以及未知分布$q_{[T]}(z)$，当$x\sim p(x)$时，有
$${\nabla }_{ϵ}KL(q_{[T]}||p){|}_{ϵ=0}=-{\mathbb{E}}_{x\sim q}[tr({\mathcal{A}}_p\varphi (x))]\text{\hspace{1em}(5)}$$证明如下：

Note:

1. ${\mathcal{A}}_p\varphi (x)=s_p\varphi (x{)}^T+{\nabla }_x\varphi (x)$
2. 这里和KSD的原论文相反，这里是$q$未知，为估计分布，$p$已知，为目标分布。
3. 等式左边涉及到泛函导数、变分法的知识，变分法是专门用于处理泛函问题的工具，相当于微积分法是专门用于处理函数问题的工具，我们要找到使得KL散度下降最快的函数$T$，这就是典型的泛函问题，我们求的是泛函极值问题，所以该问题就是变分问题。
4. 等式右边是个和KSD相关的东西，等式左边代表着KL散度的方向导数。这个怎么理解呢？根据泛函分析，左边的表达式如果等于0的话，意味着此时KL散度取得极值，但由于$ϵ=0$之后仍然会有变量$x$的存在，所以这一次你右边不会等于一个0，那$ϵ=0$出来的是什么呢？

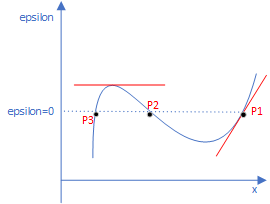
如上图所示，可以把KL散度理解为一个二元的函数$F(x,ϵ)$，实际上的图应该是个立体的，有许多个小山坡，这只是简易表示。分析：式(5)左边这是一个对$ϵ$的偏导数，即只关于$ϵ$的斜率。式(5)表达的就是点P的情况，也就是说KL散度关于$ϵ$的斜率是个和变量$x$有关的值，但可以是这条曲线上的P1、P2、P3点的斜率值，具体哪个取决于$x$的值，但如上面所说，实际上是立体图，也就是说确定了$x$，即确定了哪个P点之后，比如确定了P1，那么立体图上这个斜率是有无数多种的，沿着不同方向有不同的变化率，这其实就是方向导数！所以式(5)就是方向导数，一看到方向导数，就想到了梯度，它是方向导数的最大值，也是变化率最大的方向，巧的是式(5)右边就是个能进行优化求出最大值的表达式，当$\varphi (x)$取特定的值，右边就能达到最大。至于这个“负号”，并不碍事，我们在利用式(5)的时候，只是表示从上升最快转成下降最快而已，这样便于KL梯度下降，梯度的反方向就是下降最快的方向。

Lemma 3.2.
如果所有的方向$\varphi (x)$都在球内： B = { ϕ ∈ H d : ∣ ∣ ϕ ∣ ∣ H d 2 ≤ S ( q , p ) } \mathcal{B}=\{\phi\in\mathcal{H}^d:||\phi||^2_{\mathcal{H}^d}\leq\mathbb{S}(q,p)\} B={ϕ∈Hd:∣∣ϕ∣∣Hd2​≤S(q,p)}，则在这些方向中能最大化式(5)中那个负梯度的方向为：
$${\varphi }^{\ast }(\cdot )={\mathbb{E}}_{x\sim q}[s_p(x)k(x,\cdot )+{\nabla }_{x}k(x,\cdot )]={\mathbb{E}}_{x\sim q}[{\mathcal{A}}_{p}k(x,\cdot )]\text{\hspace{1em}(6)}$$Note:

1. $\varphi =\varphi (\cdot ),k(x,\cdot )$都表示向量。
2. $s_p$为Stein得分函数。
3. 这个引理来自于KSD那篇论文的Theorem3.8。
4. 式(6)和论文中的不太一样，从我的理解角度看，论文中表达的意思应该就是我这里式(6)写的那样。
5. 当$\varphi ={\varphi }^{\ast }$的时候，式(5)就相当于：${\nabla }_{ϵ}KL(q_{[T]}||p){|}_{ϵ=0}=-\mathbb{S}(p,q)$。换句话说当$\varphi ={\varphi }^{\ast }$的时候，是KL散度下降最快的方向。

当$\varphi$取最优值${\varphi }^{\ast }$的时候，只要变量沿着方向${\varphi }^{\ast }$移动$ϵ\cdot \mathbb{S}(q,p)$，就可以使得KL散度以最快的速度下降(从这里也看出了$\varphi (x)$代表着方向)。同时，平滑转换$T=x+ϵ\cdot {\varphi }^{\ast }(x)$。总的流程用一个动态过程表示为：
起始分布$q_0$；
第一次梯度下降：$T_0^{\ast }(x)=x+{ϵ}_0\cdot {\varphi }_{q_0,p}^{\ast }(x);q_1(x)=q_{0[T_0^{\ast }]}(x)$；
第二次梯度下降：$T_1^{\ast }(x)=x+{ϵ}_1\cdot {\varphi }_{q_1,p}^{\ast }(x);q_2(x)=q_{1[T_1^{\ast }]}(x)$；
… … …直至收敛
总结起来就是：
$$q_{l+1}=q_{l[T_l^{\ast }]}，T_l^{\ast }(x)=x+{ϵ}_l\cdot {\varphi }_{q_l,p}^{\ast }(x)\text{\hspace{1em}(7)}$$Note:

1. $T,q$的不断迭代也显示了平滑转换一对一性的重要，因此$ϵ$要足够小。
2. 最终KL散度会因为不断减小而为0，$q$会收敛到目标分布$p$，当且仅当${\varphi }_{p,q^{\infty }}^{\ast }(x)=0$

Functional Gradient(泛函梯度)
设$\mathbf{f}、\mathbf{g}\in {\mathcal{H}}^d$，则$F[f]$就是泛函，${\nabla }_{\mathbf{f}}F[\mathbf{f}]$就是泛函梯度，其有如下结论：$$F[\mathbf{f}+ϵ\mathbf{g}(x)]=F[f]+ϵ<{\nabla }_{\mathbf{f}}F[\mathbf{f}],\mathbf{g}{>}_{{\mathcal{H}}^d}+O({ϵ}^2)$$。
Theorem 3.3.
设$T(x)=x+\mathbf{f}(x),x\in {\mathbb{R}}^d,\mathbf{f}\in {\mathcal{H}}^d$，则：
$${\nabla }_{\mathbf{f}}KL(q_{[T]}||p){|}_{\mathbf{f}=0}=-{\varphi }_{q,p}^{\ast }(x)$$Note:

1. 这个式子我最终没有证明出来，看过作者在补充材料的证明是有问题的，要么就是矩阵向量前后大小对不上，要么就是最后部分漏东西，最后$\mathbf{f}=0$带进去也是得不出${\varphi }^{\ast }={\mathbb{E}}_{x\sim q(x)}[{\mathcal{A}}_{p}k(x,\cdot )]$这个结果的，只能证明到${\mathbb{E}}_{x\sim q(x)}[tr({\mathcal{A}}_{p}k(x,\cdot ))]$。
2. 以下是我的证明：接下来需要用到向量矩阵的Taylor展开(和高数中的略有不同)：
   总之感觉作者在凑这个${\varphi }^{\ast }$，这个Theorem 3.3应该算错的，因此下面关于这个定理的就不分析了。不过好在这个定理的好坏并不影响Algorithm1，即Stein变分梯度下降。
3. 另外需要注意的是，我们一般向量内积或者矩阵内积的结果都是实值，默认都是大小一样的且向量必须同为行或者列向量，矩阵内积必须均为方阵。如果$<A,B>$运算的A和B(向量和向量、向量和矩阵)大小不一样，则输出的结果就不一定是实值了，可能是向量或者矩阵。

3.2 Stein Variational Gradient Descent

算法的伪代码如下：

1. 伪码简洁明了，左边是公式(7)，不断更新粒子(可以理解成样本)来改变初始分布$q_0$。
2. 粒子 { x i l } i = 1 n \{x_i^l\}^n_{i=1} {xil​}i=1n​表示第$l$次迭代的第$i$个粒子，一个$n$个。粒子最开始是从分布$q_0$中采样的，最初的分布$q$是不准确的并且可以是任意的。也就是说，该算法不依赖于初始的分布。
3. 准确的说，粒子的统计分布就是$q(x)$。比如第$l$次迭代，统计粒子的均值、方差构成高斯分布$p(x)$。伪代码所做的就是用这些粒子去拟合目标分布$p(x)$。
4. 右边是公式(6)的近似表示，用样本均值作为期望的估计值，这是常用的做法了。
5. 算法模仿了我们所熟知的梯度上升，之前说过，$\varphi$代表了梯度方向，为KL散度下降最快的方向。该算法的梯度上升模式是粒子级别的，我们之前接触比较多的神经网络，梯度上升都是参数级别的。
6. 公式(8)的Part1和Part2类似于与探索与利用这种相互排斥的操作。首先Part1的$\nabla$部分，粒子会朝着$p$分布概率高的地方移动，但这样容易陷入局部最优，不要以为SVGD就不会陷入局部最优了，SVGD确实保证了每一步都向着KL减小最快的方向移动，这当然包括局部最小和全局最小，所以是否陷入局部最优和算法优化速度快慢是两回事。至于Part2的$\nabla$部分，作者举了个RBF核的例子：$k(x,x^{\prime })=\exp (-\frac{1}{h}||x-x^{\prime }|{|}^2)$，经过Part2的处理后：${\sum }_j\frac{2}{h}(x-x_j)k(x_j,x)$，这一项代表着粒子将会朝着远离当前迭代轮数$l$的粒子，从而减轻局部最优的风险。同样是这个高斯核，当$h\to 0$，那么这个排斥作用就没了，只剩下了Part1，那么粒子都会朝着最大化$\log p(x)$移动，这也就是MAP，从而陷入局部最优。
7. 当n=1的时候，算法就演变成了对MAP做梯度上升。
8. 算法中给出了确定性的下降方法，远远的优于传统的MCMC算法MCMC算法中使用随机性的方法来增加粒子的多样性，在Stein 变分中根本就不需要。

提高计算效率的方法
核心思想：下采样。
下采样在信号中是对于一个样值序列隔几个样值采样一次。对图像来说，下采样就是对于一副图像I尺寸为$M\times N$，对起进行s倍下采样，即得到$(M/s)\times (N/s)$尺寸的分辨率图像。通俗来说就是采样少部分的样本来近似达到大样本的效果，并且减小计算量。
公式(8)计算的瓶颈在于 ∇ x log ⁡ p ( x ) , x ∈ { x i } i = 1 n \nabla_x\log p(x),x\in\{x_i\}^n_{i=1} ∇x​logp(x),x∈{xi​}i=1n​。其中$p(x)\propto p_0(x){\prod }_{k=1}^{N}p(D_k|x)$，当数据量$N$很大的时候，计算复杂度就会很高。作者提出用下采样 Ω ⊂ { 1 , ⋯   , N } \Omega\subset\{1,\cdots,N\} Ω⊂{1,⋯,N}来近似估计${\nabla }_x\log p(x)$。本文中的下采样是这样的：
$$\log p(x)\approx \log p_0(x)+\frac{N}{|\Omega |}\sum _{k\in \Omega }\log p(D_k|x).\text{\hspace{1em}(9)}$$设${\nabla }_x\log p(x)$在全粒子上的统计结果为$R$，在下采样的表现为$G$，它的原理就是：
$$\frac{N}{\Omega }=\frac{R}{G}$$用局部代替整体。
Note：

1. 遇到大数据$N$且需要计算${\sum }_{i=1}^N$的时候，可采用下采样减小计算复杂度。

4 Related Works

略

5 Experiments

略

6 Conclusion

总结：

1. Stein变分梯度下降是这样的：首先我们需要用粒子拟合的估计分布$q(x)$通过不断迭代靠近目标分布$p(x)$，每一次迭代都是一次平滑变化$T$，平滑变化有很多种，我们要找到使得KL散度下降最快的变化方向(梯度)。因此我们的计算过程其实就优化函数中的出一个最优函数，这就是泛函问题中求泛函极值问题，我们通常使用变分法求解。
2. 本文提出的Stein变分梯度下降是结合了Stein方法，并在RKHS空间下进行梯度下降的(优化)，即使用了KSD核差异技术。
3. Stein变分梯度下降算法使用了粒子层次化的方式不断使2个分布接近一致。从上图2种优化算法的参数轨迹曲线可以看出。
4. SVGD显然比我们最先接触到的机器学习经典优化算法——SGD具有更快的收敛速度。SVGD是确定性的优化算法，而SGD是随机性的优化算法，其优化方向取决于样本，有随机性，因此稳定性会打折扣，同时收敛速度收到削弱。
5. SVGD的S指的是Stein；SGD的S指的是Stochastic。
6. SVGD是一种变分推断VI的新方法，可广泛用于快速贝叶斯推断。

Stein变分梯度下降的优缺点：
优点：

1. Stein方法通过Stein得分函数有效化解掉归一化因子。
2. Stein特征可以消除未知分布无法计算的问题。
3. 引入KSD，推导出使得KL散度下降最快的方向就是核差异方向${\varphi }^{\ast }$，这是一种确定性方向，有效增加优化的速度和效率(分析见上)。不像传统的随机性方法，需要通过随机性来增加粒子多样性。
4. 梯度方向${\varphi }^{\ast }$的近似包含正则化，避免陷入局部最优。
5. 算法不依赖于初始化粒子是怎么样的，无论如何都会走向复杂的分布，一般都是接近全局最优的局部最优。

缺点：

1. 计算复杂度高。

源码解析

关于裸的SVGD代码地址在本文顶部
main.py如下：

A = np.array([[0.2260,0.1652],[0.1652,0.6779]])
mu = np.array([-0.6871,0.8010])
model = MVN(mu, A)
x0 = np.random.normal(0,1, [10,2]);
theta = SVGD().update(x0, model.dlnprob, n_iter=1000, stepsize=0.01)
print("ground truth: ", mu)
print("svgd: ", np.mean(theta,axis=0))

1. A是目标分布的协方差，mu是目标分布的均值，model是一个二维高斯分布。
2. x0是初始分布$q_0$为一维正态分布采样的10个粒子。将10个粒子送进SVGD的核心代码(Algorithm1)中，输出经过1000次迭代后的的10个粒子分布情况，$ϵ=0.01$，他们的样本均值就是估计分布的均值。
3. 三次试验结果如下：
   ①
   ground truth: [-0.6871 0.801 ]
   svgd: [-0.68622667 0.80359776]
   ②
   ground truth: [-0.6871 0.801 ]
   svgd: [-0.68865996 0.7990209 ]
   ③
   ground truth: [-0.6871 0.801 ]
   svgd: [-0.6861909 0.80438672]

可见SVGD的有效性。