改善降质图像的方法:1.图像增强;2.图像复原
其中图像增强的主要内容如下:
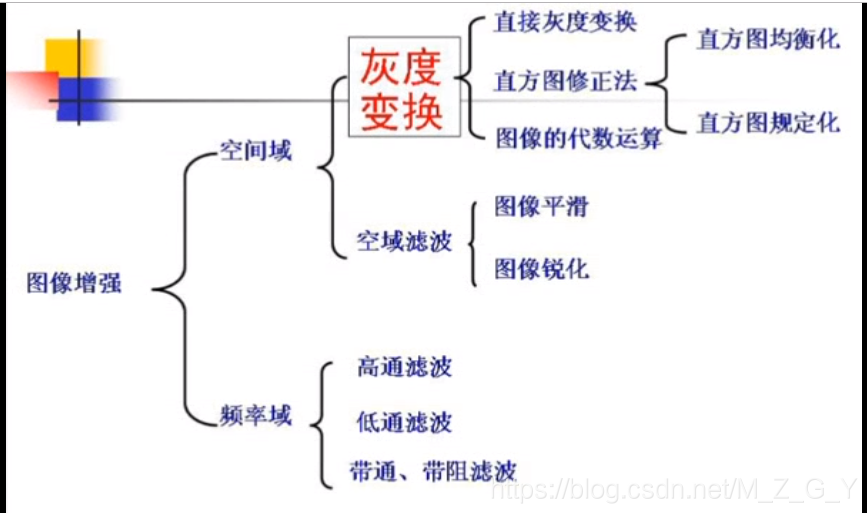
也有人将空间域变换划分为:



灰度变换也被称为图像的点运算(只针对图像的某一像素点)是所有图像处理技术中最简单的技术,其变换形式如下:s=T(r)
其中,T是灰度变换函数;r是变换前的灰度;s是变换后的像素。
图像灰度变换的有以下作用:
- 改善图像的质量,使图像能够显示更多的细节,提高图像的对比度(对比度拉伸)
- 有选择的突出图像感兴趣的特征或者抑制图像中不需要的特征
- 可以有效的改变图像的直方图分布,使像素的分布更为均匀
灰度变换函数描述了输入灰度值和输出灰度值之间变换关系,一旦灰度变换函数确定下来了,那么其输出的灰度值也就确定了。可见灰度变换函数的性质就决定了灰度变换所能达到的效果。用于图像灰度变换的函数主要有以下三种:
- 线性变换 (图像反转)</








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 7055
7055











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








