乘法器设计(二)：基于ROM的乘法器设计

最新推荐文章于 2024-01-24 13:27:38 发布

为中国IC之崛起而读书

最新推荐文章于 2024-01-24 13:27:38 发布

阅读量4.3k

点赞数 5

分类专栏： IC设计基础

本文链接：https://blog.csdn.net/MaoChuangAn/article/details/102812471

版权

本文介绍了使用ROM实现乘法器的设计原理，通过将被乘数和乘数拼接成地址，存储所有可能的乘积。针对位宽增长导致的存储空间膨胀问题，提出了位分解的优化方法，将大位宽乘法转换为多个小位宽乘法，并给出了具体的硬件结构和仿真结果。对于有符号数相乘，文章还讨论了符号扩展的处理方式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

乘法器的另一种实现思想是采用ROM的方式，即将被乘数和乘数连接起来拼成地址，把两者所有可能的乘积按照地址号存放在ROM的地址空间中，两个数相乘时，根据两者构成的地址从ROM索取乘积结果。

首先，我们来看看为啥这样是可行的。我们会有一个疑问，两者构成的地址能把所有的乘积结果都包含在内吗？我们来局个例子，比如两个两个1bit的数相乘，可能的相乘方式有0x1,0x0,1x1,1x0,一共四种相乘方式，其对应的结果也有四种,即0,0,1,0。那么如果将这四个结果存在ROM中，其实正好用01,00,11,10四个地址来寻址。因此是可以把所有的乘积结果都包含在内的。

通俗的来说，两个Nbit二进制数相乘，其结果为2Nbit，这意味着ROM的深度为2^(2N),宽度为（2N）,占用的空间大小为2^(2N)x2N。以两个4bit 的数相乘例子，其存储空间大小为256x8bit，对应的硬件结构如下图。无论是有符号数或者无符号数相乘都适用。显然随着位宽的增长，存贮空间将以指数速度膨胀，这是这个方法的一个弊端。

由于上述弊端的存在，一种改进方法就是进行位分解，将两个大位宽的数相乘分解为多个小位宽的数相乘。例如，两个4bit的数相乘，可将4bit拆成两个2bit，从而变成四个2bit数相乘。为了保证最终结果的正确性，需要对中间四个乘积结果进行移位处理。为了方便起见，以两个无符号数（11）x（6）对应的二进制（1011）x（0110）为例，以H1、H2分别表示（1011）和（0110）的高两位，以L1、L2分别表示其第两位，故：

（1011）x（0110）=（2^2*H1 +L1）*（2^2*H2 +L2）= 2^4*H1*H2 + 2^2H1*L2 + 2^2*H2*L1 + L1*L2

根据上式可其硬件结构如下图所示：

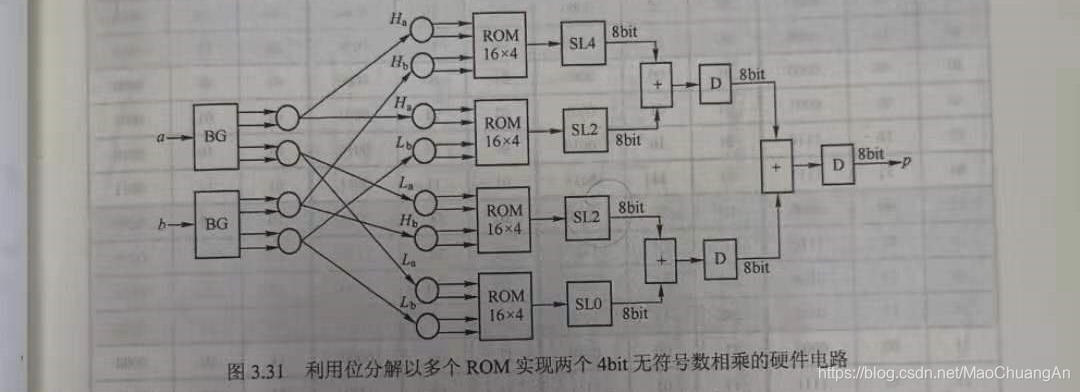
图中的 BG模块用于将数据拆成高两位和低两位。四个ROM完全相同，深度均为16，宽度均为4，存储的内容均为两个无符号数相乘的结果，如下表所示：

SL4、SL2、SL0分别是左移4位、左移2位、左移0位。由于ROM输出的是4位数，为了保证移位结果的正确性，在移位前需要对输出的4bit数进行高位补零，将其扩展为8bit。我们可以发现，这种方式只用了16x4x4bit的存储空间。是原来256x8bit的1/8，大大缩减了存储空间。

基于ROM的位分解两个4bit数相乘代码：

//顶层模块
module rom_mul(
	input							clk,
	input			[3:0]		a,
	input			[3:0]		b,
	output		[7:0]		result

    );
    
    wire		[1:0]	a_H = a[3:2];
    wire		[1:0]	a_L  = a[1:0];
    wire		[1:0]	b_H = b[3:2];
    wire		[1:0]	b_L  = b[1:0];
    
    wire		[3:0]	rom1_addr;
    wire		[3:0]	rom2_addr;
    wire		[3:0]	rom3_addr;
    wire		[3:0]	r