Frequency Pattern 频繁模式发掘(FP-growth)

Mark_Aussie

已于 2022-03-08 10:35:03 修改

阅读量999

点赞数

分类专栏：机器学习文章标签：数据挖掘

于 2021-07-05 18:14:38 首次发布

本文链接：https://blog.csdn.net/MarkAustralia/article/details/118494572

版权

机器学习专栏收录该内容

47 篇文章 5 订阅

订阅专栏

频繁模式指的是在样本数据集中频繁出现的模式。如在超市的交易系统中，有多次交易，每一次交易的信息包括用户购买的商品清单，如果发现尿不湿，啤酒这两样商品在许多用户的购物清单上都出现了，而且频率非常高，这两个商品出现在一张购物单上就可以称之为一种频繁模式，这样的发掘就可以称之为频繁模式挖掘。

Aprior 特性，如果项目集合不是频繁模式集合则任何含有此集合的项目集也不是频繁集合。

L(k)-候选项目队列，该队列中包含一系列的项目集合（也就是说队列是项目集合的集合），这些项目集合的长度是一样的，都为k，长度称为秩，这些长度相同的集合称之为k-集合。

L(k+1) = L(k) product L(k)。通过product操作（自叉积），秩为k的候选队列可以生成秩为k+1的候选队列。需要注意的是，这里所有的候选队列中的k-集合都按照字母顺序（或某种事先定义好的顺序）排好序了。product操作是针对候选队列中的k-集合的，实际上就是候选队列中的k-集合两两进行join操作。K-集合 L1，L2 之间能够进行join的前提是两个k-集合的前k-1个项目是相同的，并且l1(k)的顺序大于l2(k)(这个顺序的要求是为了排除重复结果)。

用公式表示：(l1[1]=l2[1])^(l1[2]=l2[2])^…^(l1[k-1]=l2[k-1])^(l1[k]<l2[k])，那么join的结果就形成了k+1长度的集合l1[1],l1[2],…,l1[k-1],l1[k],l2[k]。如果L(k)队列中的所有k-集合两两之间都完成了join操作，那么这些形成的k+1长度的集合就构成了一个新的秩为k+1的候选项目队列L(k+1)。

剪枝操作是针对候选队列的，对候选队列中的所有k-集合进行一次筛选，筛选过程会对数据库进行一次扫描，把那些不是频繁项目集合的k-集合从L(k)候选队列中去掉。因为不是频繁集合的k-集合通过product操作无法生成频繁集合，它们对product操作产生频繁集合没有任何贡献，把它保留在候选队列中除了增加复杂度没有任何其他优点，因此就把它从队列中去掉。

这两个操作构成了算法的核心，用户从秩为1的项目候选队列开始，通过product操作，剪枝操作生成秩为2的候选队列，再通过同样的2步操作生成秩为3的候选队列，一直循环操作，直到候选队列中所有的k-集合的出现此为等于support count.

frequent-pattern tree(频繁模式树)

一张商品交易清单，abcdefg代表商品，(ordered) frequent items 是把商品按照降序重新进行了排列，非频繁的项目在整个挖掘中不起任何作用，因此要排除了列中的非频繁项。

例子中设置最小支持阈值（minimum support threshold）为 3。

目标是为整个商品交易清单构造一颗树。根节点为null，然后扫描整个数据库构造FP树。

第一步：扫描数据库的第一个交易，也就是TID为100的交易。那么就会得到这颗树的第一个分支<(f:1),(c:1),(a:1),(m:1),(p:1)>。注意这个分支一定是要按降序排列。

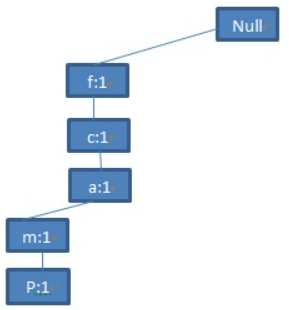
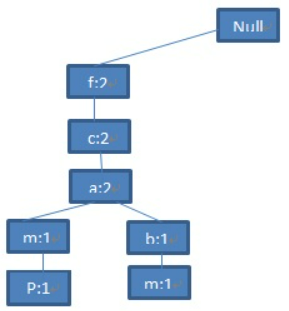
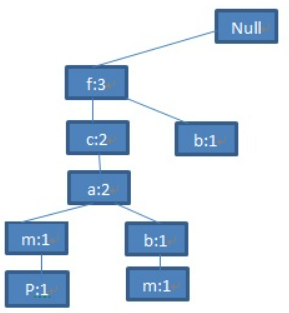
第二步：扫描第二条交易记录（TID=200），集合的前3项<f,c,a>与第一步产生的路径<f,c,a,m,p>的前三项是相同的，共享一个前缀。在第一步产生的路径的基础上，把<f,c,a>三个节点的数目加1，然后将<(b:1),(m:1)>作为一个分支加在(a:2)节点的后面，成为它的子节点。

依次构建树：

为便于树的遍历，增加头表，保存所有的频繁项目，按照频率的降序排列，表中的每个项目包含一个节点链表，指向树中和它同名的节点。

从这棵树里挖掘出所需的频繁项目集合而不需要再访问数据库了。

第一步:挖掘从头表的最后一项p开始，一个明显的直接频繁集是(p:3)了。根据 p 节点链表，它的2个节点存在于 2 条路径当中：路径< f:4,c:3,a:3,m:2,p:2 >和路径< c:1,b:1,p:1 >。从路径<f:4,c:3,a:3,m:2,p:2>发现包含p的路径<f,c,a,m,p>出现了2次，同时也会有<f,c,a>出现了3次，<f>出现了4次。但是现在只关注<f,c,a,m,p>，目的是找出包含p的所有频繁集合。同样可以得出<c,b,p>在数据库中出现了1次。于是p就有2个前缀路径{(fcam:2),(cb:1)}。

这两条前缀路径称之为p的子模式基（subpattern-base），也叫做p的条件模式基（之所以称之为条件模式基是因为这个子模式基是在p存在的前提条件下）。接下来再为这个条件子模式基构造一个p的条件FP树。再回忆一下上面FP树的构造算法，很容易得到下面这棵树：

由于频繁集的阈值是3，实际上剪枝后只剩下一个分支(c:3)，从这棵条件FP树上只能派生出一个频繁项目集{cp:3}，加上直接频繁集(p:3)就是最后的结果。

第二步:开始挖掘头表中的倒数第二项m，同第一步一样，直接的频繁集(m:3)。再查看它在FP树中存在的两条路径<f:4,c:3,a:3,m:2>和<f:4,c:3,a:3,b1,m:1>.那么它的频繁条件子模式基就是{ (fca:2),(fcab:1)}.为这个子模式基构造FP树，同时舍弃不满足最小频繁阈值的分支b，这棵FP树中只存在唯一的频繁路径<f:3,c:3,a:3>，既然这颗子FP树是存在的，并且不是一颗只有一个节点的特殊的树，继续递归挖掘这棵树，这棵子树是单路径的子树,简化写成

mine(FP tree|m)=mine(<f:3,c:3,a:3>|m:3).

下面来阐述如何挖掘这颗FP子树，这里需要递归，递归子树也需要这么几个步骤:

1. 这颗FP子树的头表最后一个节点是a,结合递归前的节点m，得到am的条件子模式基{(fc:3)}，此子模式基构造的FP树(m的子子树)也是一颗单路径树<f:3,c:3>，继续递归挖掘子子树mine(<f:3,c:3>|am:3)

2. 同样 FP子树头表的倒数第二个节点是c,结合递归前节点m，需要递归挖掘mine(<f:3>|cm:3).

3. FP子树的倒数第三个节点也是最后一个节点是f，结合递归前的m节点，实际上需要递归挖掘mine(null|fm:3)，实际上这种情况递归可以终止了，因为子树已经为空了，返回频繁集合<fm:3>

注意：这三步还包含了直接的频繁子模式<am:3>,<cm:3>,<fm:3>，在每一步递归调用mine<FPtree>都是一样的。

继续推导递归，得到下面的结果.

mine(<f:3,c:3>|am:3)=><cam:3>,<fam:3>,<fcam:3>

mine(<f:3>|cm:3)=><fcm:3>

mine(null|fm:3)=><fm:3>

这三步还都包含了各自直接的频繁子模式<am:3>,<cm:3>,<fm:3>。

最后再加上m的直接频繁子模式<m:3>，就是整个第二步挖掘m的最后的结果。

依次获得对应的FP树，结果加在一起，得到所需要的所有频繁集。

单路径的 FP 树挖掘是有规律的，通过排列组合可直接生成。对单路径的情况作优化，如果 FP 树有很长的单路径，就将这棵FP树分成两个子树：一个子树是由原FP树的单路径部分组成，另一颗子树由原FP树的除单路径之外的其余部分组成。这两个子树分别进行FP Growth算法，最后的结果组合即可。

该算法思想简单，用简洁的数据结构把整个数据库进行 FP 挖掘所需要的信息都包含了进去，通过对数据结构的递归就可以完成整个频繁模式的挖掘。由于这个数据结构的size远小于数据库，可以保存在内存中，挖掘速度可大大提高。

如果数据库足够大，以至于构造的FP树大到无法完全保存在内存中，一种思路是通过将原来的大的数据库分区成几个小的数据库(这种小的数据库称之为投射数据库)，对这几个小的数据库分别进行FP Growth算法.

如上例，把包含p的所有数据库记录都单独存成一个数据库，称为p-投射数据库，类似的m,b,a,c,f都可以生成相应的投射数据库,这些投射数据库构成的FP树就小得多,完全可以放在内存里。

可使用 pyfpgrowth 包实现频繁挖掘。

Prefix span：挖掘频繁序列模式，

项集数据在Apriori和FP Tree算法中使用，每个项集数据由若干项组成，这些项没有时间上的先后关系。而右边的序列数据则不一样，由若干数据项集组成的序列。

如第一个序列<a(abc)(ac)d(cf)>，由a,abc,ac,d,cf 5个项集数据组成，这些项有时间上的先后关系。对于多于一个项的项集要加上括号，以便和其他的项集分开。同时由于项集内部是不区分先后顺序的，为了方便数据处理，一般将序列数据内所有的项集内部按字母顺序排序。

子序列和频繁序列

子序列和数学上的子集的概念很类似，如果某个序列A所有的项集在序列B中的项集都可以找到，则A就是B的子序列。对于序列A={a1,a2,...an} 和序列 B={b1,b2,...bm}, n≤m，如果存在数字序列1≤j1≤j2≤...≤jn≤m, 满足a1⊆bj1,a2⊆bj2...an⊆bjn，则称A是B的子序列，B就是A的超序列。

而频繁序列则与频繁项集很类似，频繁出现的子序列。如下图，支持度阈值定义为50%，也就是需要出现两次的子序列才是频繁序列，而子序列<(ab)c>是频繁序列，它是图中的第一条数据和第三条序列数据的子序列，对应的位置用蓝色标示。

PrefixSpan算法全称 Prefix-Projected Pattern Growth，即前缀投影的模式挖掘。

在PrefixSpan中的前缀prefix通俗意义讲就是序列数据前面部分的子序列。

对于序列A={a1,a2,...an} 和序列 B={b1,b2,...bm}，n ≤ m，满足a1= b1, a2=b2...an−1=bn−1,而an⊆bn，则称A是B的前缀。如序列数据B=<a(abc)(ac)d(cf)>，而A=<a(abc)a>，则A是B的前缀，B的前缀不止一个，比如<a>, <aa>, <a(ab)> 也都是B的前缀。

前缀投影就是后缀，前缀加上后缀就可以构成一个序列。对于某个前缀，序列里前缀后面剩下的子序列即为后缀。如果前缀最后的项是项集的一部分，则用一个“_”来占位表示。

下面例子展示序列<a(abc)(ac)d(cf)>的一些前缀和后缀。注意，如果前缀的末尾不是一个完全的项集，则需要加一个占位符。PrefixSpan 中相同前缀对应的所有后缀的结合称为前缀对应的投影数据库。

PrefixSpan算法的目标是挖掘出满足最小支持度的频繁序列。Aprior算法从频繁1项集出发，一步步的挖掘2项集，直到最大的K项集。PrefixSpan算法也类似，从长度为1的前缀开始挖掘序列模式，搜索对应的投影数据库得到长度为1的前缀对应的频繁序列，然后递归的挖掘长度为2的前缀所对应的频繁序列，一直递归到不能挖掘到更长的前缀挖掘为止。

如上例，支持度阈值为50%。长度为1的前缀包括<a>, <b>, <c>, <d>, <e>, <f>,<g>，需要对这6个前缀分别递归搜索找各个前缀对应的频繁序列。如下图所示，每个前缀对应的后缀也标出来了。由于g只在序列4出现，支持度计数只有1，因此无法继续挖掘。长度为1的频繁序列为<a>, <b>, <c>, <d>, <e>，<f>。去除所有序列中的g，即第4条记录变成<e(af)cbc>。

开始挖掘频繁序列，分别从长度为1的前缀开始。以d为例递归挖掘，先对ｄ的后缀进行计数，得到{a:1, b:2, c:3, d:0, e:1, f:1，_f:1}。注意 f 和 _f 是不一样的，因为前者是在和前缀 d 不同的项集，而后者是和前缀d同项集。此时a,d,e,f,_f 都达不到支持度阈值，因此递归得到的前缀为d的2项频繁序列为<db>和<dc>。接着分别递归db和dc为前缀所对应的投影序列。首先看db前缀，此时对应的投影后缀只有<_c(ae)>，_c,a,e支持度均达不到阈值，无法找到以db为前缀的频繁序列。再递归另外一个前缀dc。以dc为前缀的投影序列为<_f>, <(bc)(ae)>, <b>，此时进行支持度计数{b:2, a:1, c:1, e:1, _f:1}，只有b满足支持度阈值，因此得到前缀为dc的三项频繁序列为<dcb>。继续递归以<dcb>为前缀的频繁序列。由于前缀<dcb>对应的投影序列<(_c)ae>支持度全部不达标，因此不能产生4项频繁序列，因此以d为前缀的频繁序列挖掘结束，产生的频繁序列为<d><db><dc><dcb>，同样的方法可以得到其他以<a>, <b>, <c>, <e>, <f>为前缀的频繁序列。