皮尔森相关系数
线性相关,皮尔逊相关系数是用来衡量两个变量之间线性相关程度的指标。取值范围在-1到1之间,负值表示负相关,正值表示正相关,0表示两个变量之间没有线性关系。但当变量之间存在非线性关系时,皮尔逊相关系数的效果就变差了。
pandas中的corr()方法可使用如下方法,检测特征间的关系

计算公式:两个连续变量(X,Y)的pearson相关性系数(Px,y)等于(X, Y)的协方差cov(X,Y)除以各自标准差的乘积(σX,σY)。
系数取值在-1.0到1.0之间,接近0的变量被成为无相关性,接近1或者-1被称为具有强相关性。
def pearson(vector1, vector2):
n = len(vector1)
# simple sums
sum1 = sum(float(vector1[i]) for i in range(n))
sum2 = sum(float(vector2[i]) for i in range(n))
# sum up the squares
sum1_pow = sum([pow(v, 2.0) for v in vector1])
sum2_pow = sum([pow(v, 2.0) for v in vector2])
# sum up the products
p_sum = sum([vector1[i]*vector2[i] for i in range(n)])
# 分子num,分母den
num = p_sum - (sum1*sum2/n)
den = math.sqrt((sum1_pow-pow(sum1, 2)/n)*(sum2_pow-pow(sum2, 2)/n))
if den == 0:
return 0.0
return num/den
皮尔森相关系数对数据是有比较高的要求的:
第一, 实验数据通常假设是成对的来自于正态分布的总体。因为在求皮尔森相关性系数以后,通常还会用 t 检验等方法来进行皮尔森相关性系数检验,而 t 检验是基于数据呈正态分布的假设的。
第二, 实验数据之间的差距不能太大,或者说皮尔森相关性系数受异常值的影响比较大。
例如心跳与跑步的例子,如果心脏不好,跑到一定速度后承受不了,突发心脏病,就会测到一个偏离正常值的心跳(过快或者过慢,甚至为0),如果加入这个值相关性分析,会干扰计算结果。
斯皮尔曼相关系数
衡量两个变量依赖性的非参数指标。常用希腊字母 ρ 表示,用单调方程评价两个统计变量相关性。如果数据中没有重复值, 并且当两个变量完全单调相关时,斯皮尔曼相关系数则为+1或−1。
斯皮尔曼相关系数是一种非参数指标,用于衡量两个变量之间的单调关系。单调关系指的是如果一个变量增加,那么另一个变量也会增加(单调正相关),或者如果一个变量增加,那么另一个变量会减少(单调负相关)。
斯皮尔曼相关系数的取值范围在-1到1之间,越接近1或-1表示两个变量之间的单调关系越强,0表示两个变量之间没有单调关系。斯皮尔曼相关系数的取值为正,则说明两个变量呈单调正相关,如果斯皮尔曼相关系数的取值为负,则说明两个变量呈单调负相关。
斯皮尔曼相关系数被定义成等级变量之间的皮尔逊相关系数。对于样本容量为n的样本,n个原始数据被转换成等级数据。斯皮尔曼等级相关是根据等级资料研究两个变量间相关关系的方法。依据两列成对等级的各对等级数之差来进行计算的,所以又称为“等级差数法”。
斯皮尔曼相关系数适用于非线性或有序数据的情况。斯皮尔曼相关系数的计算基于秩次,将原始数据替换为相应的秩次,然后计算秩次间的皮尔逊相关系数。由于秩次本身不受异常值的影响,因此斯皮尔曼相关系数对异常值具有更好的鲁棒性。
数据要求
两个变量的观测值是成对的等级评定资料;
或由连续变量观测资料转化得到的等级资料;
不论两个变量总体分布形态、样本容量的大小如何,都可用斯皮尔曼等级相关来进行研究。反映两组变量之间联系的密切程度,取值在-1到+1之间,是建立在等级的基础上计算的。
等级相关系数和通常的相关系数一样,与样本的容量有关,尤其在样本容量较小的情况下,其变异程度较大,等级相关系数的显著性检验与普通的相关系数的显著性检验相同。
斯皮尔曼相关性系数,通常也叫斯皮尔曼秩相关系数。“秩”,可以理解成就是一种顺序或者排序,根据原始数据的排序位置进行求解,这种表征形式就没有了求皮尔森相关性系数时那些限制。
计算公式:

无论X和Y 两个变量的值差多少,只需计算每个值所处的排列位置的差值,就可求出相关性系数。变量值没有变化时,也不会出现像皮尔森系数那样分母为 0 而无法计算的情况。
如果出现异常值,由于秩次通常不会有明显的变化(比如过大或者过小,那要么排第一,要么排最后),所以影响也非常小。由于没有那些数据条件要求,适用的范围就广多了。
数据的秩次转换
斯皮尔曼相关系数基于秩次转换。将数据集从小到大排序,给每一个数据赋予相应排名的秩次,如果有多个数据相等,则相应的秩次是这些数据的平均值。例如,对于数据集[8, 3, 6, 7, 6, 9, 2],排序后为[2, 3, 6, 6, 7, 8, 9],则秩次分别为[1, 2, 4.5, 4.5, 6, 7, 8]。
将每个数据转换为其对应的秩次之后,计算秩次间的皮尔逊相关系数。
适用范围
当变量之间存在非线性关系时,皮尔逊相关系数可能会低估或高估它们之间的相关性。斯皮尔曼相关系数则基于秩次计算,能够更好地反映这种关系。
当变量具有有序性时,斯皮尔曼相关系数能够更好地反映它们之间的关系。例如,在医学研究中,通常需要比较不同治疗方法对疾病治愈率的影响。此时治愈率是一个有序变量,斯皮尔曼相关系数能够准确地衡量不同治疗方法之间的差异。
斯皮尔曼与皮尔斯的结果不同
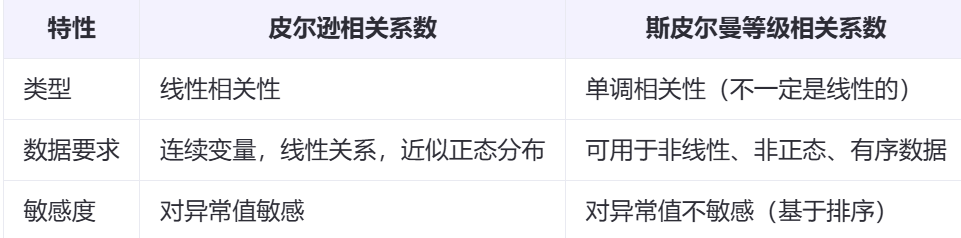
情况1:线性关系强,但有异常值
- 皮尔逊相关系数可能被异常值拉低(或抬高)
- 斯皮尔曼由于基于排序,受影响较小
情况2:非线性但单调关系
- 如:A 增加,B 也增加,但不是线性增长(比如指数关系)
- 皮尔逊相关系数可能较低
- 斯皮尔曼相关系数较高
情况3:非单调关系
- 如:A 增加,B 先增加后减少
- 两者都可能给出低相关性,但不能反映真实关系
肯德尔相关系数
经常用希腊字母τ(tau)表示,肯德尔相关系数用来测量两个随机变量相关性的统计值。
肯德尔检验是一个无参数假设检验,使用计算而得的相关系数去检验两个随机变量的统计依赖性。
肯德尔相关系数的取值范围在-1到1之间,当τ为1时,表示两个随机变量拥有一致的等级相关性;
当τ为-1时,表示两个随机变量拥有完全相反的等级相关性;当τ为0时,表示两个随机变量是相互独立的。




参考:





 本文介绍了皮尔森、斯皮尔曼及肯德尔三种相关系数的概念、计算方法及其适用场景。皮尔森相关系数衡量线性相关性,适用于正态分布数据;斯皮尔曼相关系数基于秩次计算,适合非线性和有序数据;肯德尔相关系数适用于等级数据的相关性检验。
本文介绍了皮尔森、斯皮尔曼及肯德尔三种相关系数的概念、计算方法及其适用场景。皮尔森相关系数衡量线性相关性,适用于正态分布数据;斯皮尔曼相关系数基于秩次计算,适合非线性和有序数据;肯德尔相关系数适用于等级数据的相关性检验。
















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








