ST算法求解区间最值(简介) RMQ

思想：

F[i, j]  指代由第i个数出发, 到第i+2^j个数,这段区间[i, i+2^j]的最值,    F[i, 0] => 本身    (构造需要接近O(n) )

查询:

若查询区间[s, e]最值，   则可根据上述F求出

int nlog = (log(double(e-s+1))/log(2.0)  =>  求区间[s, e]的长度>=2^m中的 m值

如 区间【s, e】最大值 = max(F[s][nlog], F[e-(1<<nlog)+1][nlog])

F[s][nlog]  =>  指区间[s, s+2^nlog]的最值  其中s+2^nlog<=e;                      

F[e-(1<<nlog)+1][nlog] => 区间 [e-2^nlog+1, e]  其中 e-2^nlog+1>=s          

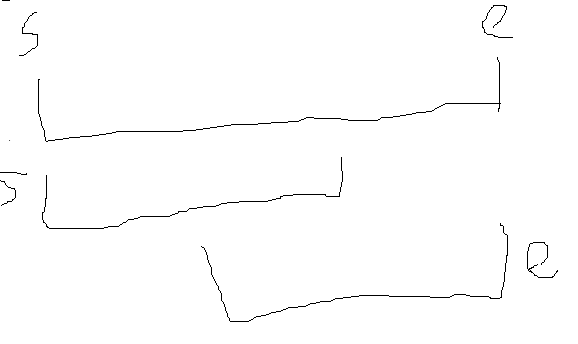
已知两个区间如下图

即两个区间是相交的且两个区间的并集 = [s, e]

Code:

void st(){
	int len = strlen(num);
	rep(i, 0, len){
		F[i][0] = num[i];
	}
	int nlog = (int)(log((double)len)/log(2.0));
	for(int j=1; j<=nlog; j++){
		for(int i=0; i+(1<<j)-1<len; i++){
			F[i][j] = min(F[i][j-1], F[i+(1<<(j-1))][j-1]);
		}
	}
	return ;
}
int RMQ(int s, int e){
	int nlog = (int)(log(double(e-s+1))/log(2.0));
	return min(F[s][nlog], F[e-(1<<nlog)+1][nlog]);
}