从神经网络基础到量化投资应用
疫情当前,国难当头,当灾难来临的时候才深刻的感觉到了自己的弱小,对国家,对亲人,是这么的无能为力,希望做点什么,可是却什么也做不了。不过庆幸的是我们还年轻,现在也不是自怜自哀的时候,作为一名学生现在可以做的就是尽快的成长起来,强大自己。在国家、亲人需要的时候说一声我可以做点什么。
知识的本身在于分享,分享的过程也是自己理解的一个加深。希望和大家一起学习,一起进步。本部分内容是一个系统内容,分为了三个章节:(这篇为第一章第一节)
- 第一章:神经网络基础知识
- 第二章:Tensorflow
- 第三章:深度学习与量化投资
基本上是遵循了从原理到实现再到应用的一个过程,第一章是从logistic入手介绍神经网络的基础知识,到卷积神经网络,再到循环神经网络。第二章为tensorflow的介绍,其实在第一章的部分会涉及一些,但是更多在第二章中,主要从tensorflow的计算模式,储存模式,到实现CNN、RNN然后再到自己搭建。第三章主要为应用,会用具体的实例来观察深度学习在金融领域的表现。这是目前的一个基本框架,如果有变动会在之后的文章中体现。
【第一章】神经网络基础知识
第一章神经网络基础知识,本章一共分为了5个节,从神经网络的介绍到序列模型,在原理部分只需要一点点简单的线性代数和高数的知识。所以Don‘t worry
一、神经网络与深度学习
本篇文章是第一章第一节,主要是通过logistics回归模型引入神经网络的基本概念,介绍了梯度下降,前向传播,反向传播等在之后的部分会经常用到的基础知识。
- 目录
- 1、简介
- 2、神经网络基础理解
- 3、单隐藏层的神经网络
- 4、深度神经网络
1、简介
1.1 理解
假设我们想要构建一个模型来表示房价和房子大小的关系,图中红色的点为实际的数据的数据点。现在构建一个回归模型来预测房子的价格,可以得到图中的蓝线。但是房价并不可能是负的,所以在接近x轴时出现拐点。房子的大小既是一个输入,价格为输出。

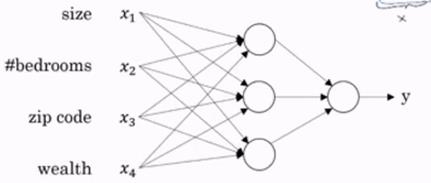
现在假设房子的价格不仅由房子的大小决定,而是由卧室的数量,邮政编码,周边的富裕的程度相关。我们可以画出如下的模型图,该图称为神经网络中的计算图,以后的模型基本都通过计算图表示,这个模型就可以简单的称一个神经网络,其中x为输入层,y为输出层,中间的部分为隐藏层。神经网络的工作既是学习中间的隐藏部分。
1.2 监督学习
监督学习既是通过输入特征x来进行模型的学习即为监督学习,即有特征的学习,常见的监督学习有图像识别、语音识别、机器翻译、自动驾驶、时间序列等。无监督学习即不需要(x,y)这样的数据集,通常的应用有聚类、降维等。神经网络为一种监督学习,常见的应用如下:
| Input(x) | Output(y) | Application | NN |
|---|---|---|---|
| Home features | Price | Real Estate | std NN |
| Ad,user info | Click on ad?(0/1) | Online Advertising | std NN |
| image | Object(1,……,1000) | Photo tagging | CNN |
| Audio | Text transcript | Speech regognition | RNN |
| Englist | Chinese | Maching translation | RNN |
| Image,Reader info | Position of other cars | Autonomous driving | hybrid NN |
2、神经网络基础
现在我们知道了神经网络是一种监督学习,是一个通过学习隐藏层从而输入数据就可以得到输出的模型,下面我们通过一个二分类问题来了解神经网络组成部分和它是怎么进行“学习”的。
- 目录
- 2.1 二分类问题
- 2.2 logistics回归
- 2.3 梯度下降法
- 2.4 计算图
- 2.5 logistics回归中的梯度下降法
- 2.6 向量化
- 2.7 Python中的传播
- 2.8 logistic损失函数的解释
2.1 二分类问题
二分类问题,顾名思义它的输出只有两个即0和1。我们的目的是输入一张图片,去判断这个图片中是否有猫(0没有,1有)。
首先来了解一下一个图片在计算机中是如何表示的,如果一张图片是64x64像素,则会有3个64x64的矩阵(红、绿、蓝),矩阵中的每一个元素为该颜色的强度。然后把每个矩阵中的元素都“拉平”、依次排开,则三个矩阵就转化为了一个12288(64x64x3)x1的特征向量X,X即为该图片的特征输入。

现在为了之后表述,做一个记号的规定
- Notation
i n p u t : ( x , y ) x ∈ R n x y ∈ 0 , 1 t r a i n i n g s e t : { ( x ( 1 ) , y ( 1 ) ) ( x ( 2 ) , y ( 2 ) ) . . . ( x ( m ) , y ( m ) ) } w h e r e : m = m t r a i n o r i n p u t s e t : X = { ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ x ( 1 ) x ( 2 ) . . . x ( m − 1 ) x ( m ) ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ } X ∈ R n x × m Y = [ y ( 1 ) , y ( 2 ) , . . . , y ( m ) ] y ∈ R 1 × m input: (x,y) x \in R^{n_x} y\in{0,1} \\ {~}\\ training set: \{(x^{(1)},y^{(1)})\, (x^{(2)},y^{(2)})\ ... (x^{(m)},y^{(m)})\} \\ {~}\\ where:m=m_{train} \\ {~}\\ or \,\, input \,\, set : \\ {~}\\ X= \left\{ \begin{matrix} | & | & | & | & | \\ | & | & | & | & | \\ x^{(1)} & x^{(2)} & ... & x^{(m-1)} & x^{(m)} \\ | & | & | & | & | \\ | & | & | & | & | \\ \end{matrix}\right\} \\ {~}\\ X \in R^{n_x \times m} \\ {~}\\ Y=[y^{(1)},y^{(2)},...,y^{(m)}] \\ {~}\\ y \in R^{1 \times m} input:(x,y)x∈Rnxy∈0,1 trainingset:{ (x(1),y(1))(x(2),y(2)) ...(x(m),y(m))} where:m=mtrain orinputset: X=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∣∣x(1)∣∣∣∣x(2)∣∣∣∣...∣∣∣∣x(m−1)∣∣∣∣x(m)∣∣⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫ X∈Rnx×m Y=[y(1),y(2),...,y(m)] y∈R1×m
2.2 logistics回归
- 2.2.1 logistics回归简述
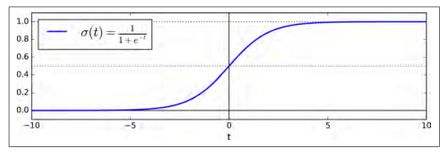
给 出 x , 预 测 y ^ = P ( y = 1 ∣ x ) x ∈ R n x 参 数 : w ∈ R n x b ∈ R 输 出 : y ^ = w T x + b 但 是 我 们 需 要 输 出 的 y ^ 是 一 个 0 − 1 之 间 的 数 所 以 需 要 引 入 σ 变 换 。 所 以 l o g i s t i c 回 归 模 型 可 以 表 示 为 : y ^ = σ ( w T x + b ) = σ ( z ) z = w T x + b w h e r e σ ( z ) = 1 1 + e − z 机 器 学 习 的 主 要 内 容 既 是 学 习 上 述 内 容 的 w 和 b , 下 面 来 了 解 怎 么 学 习 w 和 b 。 给出 x ,预测\hat{y}=P(y=1|x) \quad x \in R^{n^x} \\ {~}\\ 参数:w \in R^{n^x} \quad b \in R \\ {~}\\ 输出: \hat{y} = w^Tx + b \\ {~}\\ 但是我们需要输出的\hat{y}是一个0-1之间的数所以需要引入\sigma变换。\\ {~}\\ 所以logistic回归模型可以表示为:\\ {~}\\ \hat{y} =\sigma(w^Tx + b)=\sigma (z) \\ {~}\\ z=w^Tx + b {~}\\ where \quad \sigma(z)=\frac{1}{1+e^{-z}} \\ {~}\\ 机器学习的主要内容既是学习上述内容的w和b,下面来了解怎么学习w和b。 给出x,预测y^=P(y=1∣x)x∈Rnx 参数:w∈Rnxb∈R 输出:y^=wTx+b 但是我们需要输出的y^是一个0−1之间的数所以需要引入σ变换。 所以logistic回归模型可以表示为: y^=σ(wTx+b)=σ(z) z=wTx+b whereσ(z)=1+e−z1 机器学习的主要内容既是学习上述内容的w和b,下面来了解怎么学习w和b。
- 2.2.2 代价函数(cost function)
现在我们要得到就是有一个输入,可以得到输出。但是我们怎么知道输出是正确的?所以,需要通过训练集,把已知输出(肯定有猫)的数据进行输入,用预测值(有猫,或者是没猫)和真实值(有猫)进行比较,如果不一致则进行参数调整。如果一致则什么都不做。数据是多维的,这样的比较我们会进行很多次直到出错的概率非常小,代价函数既是预测准确度的一个体现。
l o g i s t i c m o d e l : y ^ = σ ( w T x + b ) w h e r e σ ( z ) = 1 1 + e − z g i v e n S e t : { ( x ( 1 ) , y ( 1 ) ) ( x ( 2 ) , y ( 2 ) ) . . . ( x ( m ) , y ( m ) ) } w a n t y ^ ( i ) ≈ y i 进 行 预 测 值 和 正 式 值 的 比 较 , 则 自 然 想 到 损 失 函 数 ( l o s s f u n c t i o n ) : L ( y ^ , y ) = 1 2 ( y ^ − y ) 2 但 是 该 损 失 函 数 是 非 凸 ( 找 不 到 最 好 的 点 ) 的 , 所 以 我 们 构 建 如 下 损 失 函 数 。 L ( y ^ , y ) = − ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) 上 面 的 损 失 函 数 表 示 是 单 个 数 据 的 损 失 。 现 在 我 们 来 使 用 代 价 函 数 ( c o s t f u n c t i o n ) 表 示 总 训 练 集 的 误 差 : J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) ] logistic \,\, model: \\ {}\\ \hat{y} =\sigma(w^Tx + b) \\ {}\\ where \quad \sigma(z)=\frac{1}{1+e^{-z}} \\ {}\\ given \quad Set: \{(x^{(1)},y^{(1)})\, (x^{(2)},y^{(2)})\ ... (x^{(m)},y^{(m)})\} \\ {}\\ want \quad \hat{y}^{(i)} \approx y^{i} \\ {}\\ 进行预测值和正式值的比较,则自然想到损失函数(loss function): \\ {} \\ L(\hat{y},y)=\frac{1}{2}(\hat{y}-y)^2 \\ {} \\ 但是该损失函数是非凸(找不到最好的点)的,所以我们构建如下损失函数。\\ {}\\ L(\hat{y},y)=-(ylog\hat{y}+(1-y)log(1-\hat{y})) \\ {}\\ 上面的损失函数表示是单个数据的损失。\\ {} \\ 现在我们来使用代价函数(cost function)表示总训练集的误差:\\ {} \\ J(w,b) =\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[(ylog\hat{y}+(1-y)log(1-\hat{y}))] logisticmodel:y^=σ(wTx+b)whereσ(z)=1+e−z1givenSet:{ (x(1),y(1))(x(2),y(2)) ...(x(m),y(m))}wanty^(i)≈yi进行预测值和正式值的比较,则自然想到损失函数(lossfunction):L(y^,y)=21(y^−y)2但是该损失函数是非凸(找不到最好的点)的,所以我们构建如下损失函数。L(y^,y)=−(ylogy^+(1−y)log(1−y^))上面的损失函数表示是单个数据的损失。现在我们来使用代价函数(costfunction)表示总训练集的误差:J(w,b)=m1i=1∑mL(y^(i),y(i))=−m1i=1∑m[(ylogy^+(1−y)log(1−y^))]
2.3 梯度下降法
代价函数我们已经了解了,接下来我们需要去找代价函数最小的点,从而得到对应参数w,b,梯度下降法既是一种寻找最优点的方法。在凸问题当中由导数的定义可知,w和b的梯度的方向是最快达到最优点的方向。所以我们沿着梯度的方向进行迭代。由下图可知,图中的任意一点到最小点的最快的方向既是导数的方向。多维向量的导数既是梯度。
y ^ = σ ( w T x + b ) σ ( z ) = 1 1 + e − z J ( w , b ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ ( y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ) ] \hat{y} =\sigma(w^Tx + b) \quad \sigma(z)=\frac{1}{1+e^{-z}} \\ {}\\ J(w,b) =\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)},y^{(i)}) =-\frac{1}{m}\sum_{i=1}^{m}[(ylog\hat{y}+(1-y)log(1-\hat{y}))] \\ {} \\ y^=σ(wTx+b)σ(z)=1+e−z1J(w,b)=m1i=1∑mL(y^(i),y(i))=−m1i=1∑m[(ylogy^+(1−y)log(1−y^))]

所以w和b的更新方程为:
w : = w − α d J ( w , b ) d w b : = b − α d J ( w , b ) d b α 称 为 学 习 率 w:=w-\alpha \frac{dJ(w,b)}{dw} \\ {} \\ b:=b-\alpha \frac{dJ(w,b)}{db} \\ {}\\ \alpha 称为学习率 w:=w−αdwdJ(w,b)b:=b−αdbdJ(w,b)α称为学习率
2.4 计算图
接下来我们来看怎么在模型中有步骤的完成上述过程。
计算图为神经网络的计算模型,计算图可以很好的表示神经网络模型,在神经网络中必不可少,在接下的计算过程中,我们会一直用到计算图。神经网络的计算过程主要分为前向传播和反向传播。
- 前向传播,即从输入到输出的过程
例 如 模 型 : J ( a , b , c ) = 3 ( a + b c ) 令 u = b c v = a + u j = 3 v 例如模型:J(a,b,c)=3(a+bc)\\ {}\\ 令 u = bc\\ {}\\ v = a+u \\ {} \\ j = 3v \\ 例如模型:J(a,b,c)=3(a+bc)令u=bcv=a+uj=3v
则前向传播的计算图表示为:
- 反向传播
反向传播既利用最后的结构向前传播,向前推出前一结构的过程,是为了用来计算w和b的更新步长,是通过导数链式法则实现。
按 照 上 面 的 模 型 : α J α V = 3 α J α a = α J α V α V α a 因 为 我 们 一 直 都 是 J 对 其 他 参 数 进 行 求 导 。 所 以 我 们 可 以 把 α J α a 记 作 α a 或 者 d a , 区 别 在 于 a 是 否 是 一 维 的 。 一 维 用 d 表 示 , 多 维 用 α 表 示 。 按照上面的模型:\\ {}\\ \frac{\alpha J}{\alpha V}=3 \\ {} \\ \frac{\alpha J}{\alpha a}=\frac{\alpha J}{\alpha V}\frac{\alpha V}{\alpha a} \\ {} \\ 因为我们一直都是J对其他参数进行求导。\\ 所以我们可以把\frac{\alpha J}{\alpha a}记作\alpha a或者da,区别在于a是否是一维的。一维用d表示,多维用\alpha 表示。 按照上面的模型:αVαJ=3αaαJ=








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 245
245











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








