计算机视觉--学习和推理（概念篇）

最新推荐文章于 2025-02-21 16:40:04 发布

Miracle_1995

最新推荐文章于 2025-02-21 16:40:04 发布

阅读量1.3k

点赞数

分类专栏：基础概念文章标签：概率与统计基础概念机器学习相关贝叶斯公式

本文链接：https://blog.csdn.net/Miracle_1995/article/details/89474379

版权

本文探讨计算机视觉中概率与统计的基础概念，包括随机变量、联合概率、边缘化、条件概率、贝叶斯公式和独立性。这些概念在图像物体分类与检测等任务中起到关键作用。通过实例说明了如何将实际问题抽象为数学模型，为理解机器学习方法打下基础。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

计算机视觉–学习和推理（概念篇）

Tips：本主要参考了《计算机视觉：模型、学习和推理》一书之中的结构，并在叙述中参入自己在平时工作中的经验和理解，有关理论和概念的描述可能并不会很严谨。

计算机视觉 的两个重要的基本问题是图像物体分类与检测，同时它们也是图像分割、物体跟踪、行为分析等其他高层视觉任务的基础[1]。在物体的分类与检测方法中，无论是传统的机器学习方法，还是深度学习的方法，够会极大地应用到概率与统计中的方法。所以，掌握统计学相关的知识和相关的数学工具对于计算机视觉的学习十分必要；因为，我们要知其然才能了解每种方法的优缺点，并作出改进。这篇文章主要会讲到以下几个方面：

基本概念 ：主要是统计学中的基础概念，后面会逐步加入信息论和共形几何方面的概念；
简单的应用 ：我会将实际工程中的分类例子抽象成简单的数学模型，供大家参考。

概率与统计基础概念

概率解释最初看起来可能比较复杂，但它有一个很大的优势：它提供了整个机器学习的通用符号，阐明了复杂模型之间的关系。

1、随机变量
随机变量–从字面上来将，可以理解为某不确定的量（有离散和连续的分别，如下图）。它可以是某个事件发生的结果，也有可能是某个物体的测量值。关于随机变量，我们要得到它的更多的信息应由其概率分布来捕获。

值得注意的是，在机器学习中，随机变量x可以是自然语言或是数字图像；这时候，x可以是这二者的任意一种形式载体，比如：一维向量、二维矩阵或者是经过卷积后的n阶张量等等。

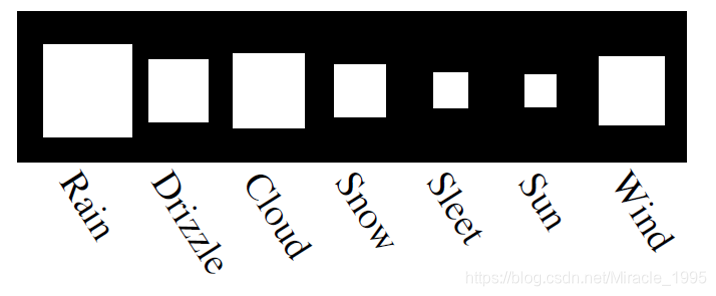
**图1.1 离散随机变量**
图1.1 离散随机变量

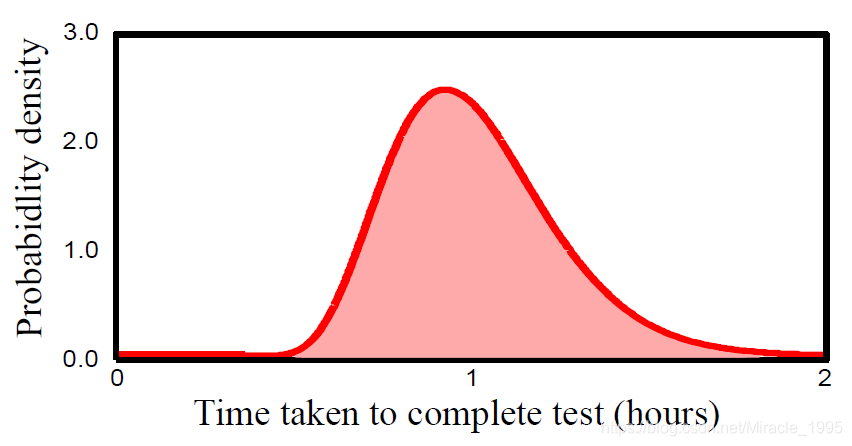
**图1.2 连续随机变量**
图1.2 连续随机变量

2、联合概率与边缘化
将上述的单个的随机变量x考虑，上升为两个随机变量x、y；由两个随机变量共同作用所产生的结果，我们用它们的联合概率来描述x和y成对结果的分布。记为： $\operatorname{Pr}(x, y) d x$ 。其中x和y都可以是离散的或是连续的。

图2.1 x、y都是连续随机变量

图2.2 二者都是离散随机变量

图2.3 一个为连续一个为离散

边缘化
即是在已知了联合概率分布的情况下，求单变量概率分布的过程：
连续变量：
$\begin{aligned} \operatorname{Pr}(x) &=\int \operatorname{Pr}(x, y) d y \end{aligned}$
离散变量：
$\operatorname{Pr}(x)=\sum_{y} \operatorname{Pr}(x, y)$