【判断推理】分析推理②

8.2 日常分析推理

日常分析：给出日常生活中蕴含逻辑关系的若干条件，需要考生抽丝剥茧找到其内在联系并适当推理，此类问题没有固定的解题方法，真正考察了考生的逻辑思维。
常用方法：代入法、画表法、画图法、赋值法等。
解题入手点：一般可以从确定信息、最大信息入手。

8.2.1 画表法

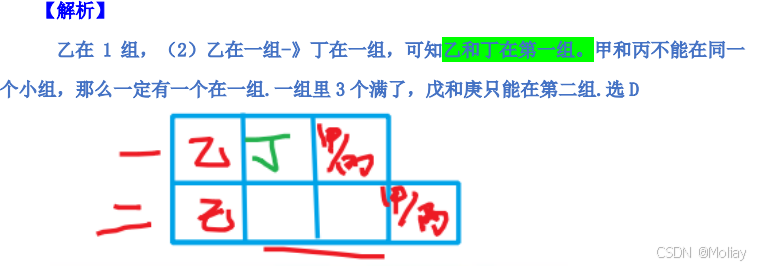
题干：乙在第一组
（4）己在第二组
（1）甲丙不在同一组，则第一组一定有甲丙中的其中一个
故第一组满了，庚在第二组
实在是优雅



题干：五个人分三个小区&每个小区1~2人
则一定是1 2 2分配
①南山人最少
则南山1人
（②信息少，跳过）③孔 || 邓 || 丁 任一人在东江，都会有北苑只有一人
则该三人一定不在东江
从而剩下的吴&洪 在东江
②吴非北苑，后件为假
则前件为假
从而邓&丁 北苑，孔 南山，故选D

推荐下图方法

8.2.2 画图法

“C摆放在D旁边” CD
“CE间隔着一个”，“CH相邻”，“D在G旁边”，EHCDG
“F在E旁边”，FEHCDG
“F与B的距离比与A的距离更近”，BFEHCDGA

找是否有信息最多的，发现丁出现的最多，三次，则能确定丁的右边是谁
即丁丙
“丁左边不是丙或戊”，则可能搁一个或两个
分别尝试填空看是否满足条件即可
其中注意，把位置数具象化，能节省后续计算量

8.2.3 赋值法

用排除法
王刚纳税额区间不确定，AB都有反例，排除
当王刚纳税额在李明赵贤中间时，不满足C，排除，故选D


按照题意进行赋值，具象大小关系
明2 + 亮4 = 川1 + 海5
川1 + 亮4 < 明2 + 海5 （川<明）
亮4 > 明2 + 川1（开始赋值）

8.2.4 特殊思维

8.2.4.1 等价思维

排除法：（做题时推荐）
只有（1）出现的黄丁，则 黄 = 丁
（2）（3）得 杨 = 贾
（2）中剩下的李肖，有 李 = 肖
回看选项BCD本质上同一个逻辑，不可能同时全队，所以全部排除，故选A

正推法：（平时理解即可，考场上不建议）
（3）杨 || 贾 → 陈，逆否命题：非陈 → 非杨 & 非贾
若非陈，由（2）知李&肖
若非李&非肖，由（2）知杨&贾，从而由（3）知陈
即陈 || 肖 一定为真

每位县领导不连续
书记和副书记不能同一天值班

则书记 = 副书记，排除AC

• 排除法
  D：周三张=王，排除，故选B
• 正推法
  周三周五分别有江和王，周四需要一个县领导值班，则只有张才能满足县领导不连续，故选B
  

8.2.4.2 极限思维

四人正确率超过一半，发现每个名次出现最多的预测超过三个的只有三个人，低于两个的有一个，加一起刚好超过一半，则只有这些人都正确才能满足超过一半，从而把其他名次的选手去掉，得出第三名

8.2.5 特殊模型

8.2.5.1 不同角度分类模型

分角度画图，知X > X - 2,即借中 > 自英，故选D


最理想的是 男师 < 女非师
C：重复题干，排除
D：女非师和男非师间的大小关系，不能完全影响男女间的大小关系，排除
A：师 < 非师，记男师y，则女非师y+，才能满足y + x < x- + y+
从而从男女角度有 y + x- < x + y+,故选A

8.2.5.2 包含关系模型

不理解，先记下来解法吧
从地方分一共三人（北方2+广东1）
从生意分一共5人（只电2 + 只服3）
当两个集合有包含关系时，人数至少的情况，有5人（max(3,5)）
当两个集合没有交集时，人数至多的情况，有8人（3 + 5）

8.2.5.3 多重身份模型

甲考上的不是农业，则甲只能是医科 || 财经
丁是湖北人，同理只能说医科 || 财经
从而乙是江苏是农业，选D


同一个材料的题，从材料中推出的信息可以共用，但由之前题目中的假设条件推出的信息，若无特别说明不能共用

8.2.5.4 数独模型

注意数独类是每行每列不能重复 or 每行每列每斜对角线不能重复，不要想当然

从最大信息处入手，发现敬业出现的最多，对于第四列，二三行不能有敬业，四行已有诚信，则④为敬业，排除ABD，选C

8.2.5.5 冠军模型

甲乙丙三个人参加一个项目，最后只有一个冠军，叫冠军模型

通过一人申请
①甲×
②乙√
③丙×
只有一个预测正确，乙通过则三个预测全对，矛盾，故选D

翻译为谁可能通过，几人预测正确，就要出现几次


只有一所中标→ 冠军模型
①甲 || 乙
②甲 || 乙 || 丁 || 戊 || 己
③甲 || 乙 || 丙 || 丁
只有一人看法正确，则出现两次及以上的一定不中标，即甲乙丁不中标，选C

end