本篇博文主要总结一下机器学习里面特征降维的方法,以及各种方法之间的联系和区别。
机器学习中我个人认为有两种途径可以来对特征进行降维,一种是特征抽取,其代表性的方法是PCA,SVD降维等,另外一个途径就是特征选择。
特征抽取
先详细讲下PCA降维的原理
对于n个特征的m个样本,将每个样本写成行向量,得到矩阵A
寻找样本的主方向u:将m个样本值投影到某个直线L上,得到m个位于直线L上的点,计算m个投影点的方差。认为方差最大的直线方向就是主方向。那么如何选取到方差最大的直线方向呢?
我们这里假定样本是中心化的,若是没有去均值化,则计算m个样本的均值,将样本真实值减去均值。
我们取投影直线L的延伸方向为u,u即为投影方向,计算矩阵A乘以方向向量u的值得:
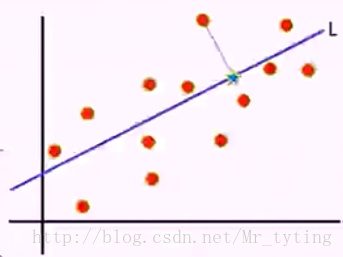
然后求向量A*u的方差,即计算投影以后的方差:
方差的计算公式为: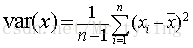
那么其目标函数即为:
回到目标本身,就是要找一个方向u使得方差最大,也就是使得上述的目标函数最大。u是个方向向量,可以加上一个约束条件,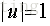
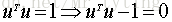
要使得目标函数最大,那么需要对u求偏导得:
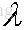
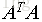
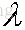
注意矩阵A表示的是n个特征的m个样本,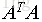
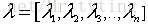
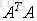
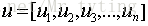
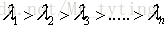
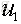
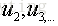
通过以上的分析可以得出,PCA其实就是寻找一个或几个投影方向,使得样本值投影以后方差最大。这种投影可以理解对特征的重构或者是组合。
利用PC降维将特征从四维降为二维,并且用多项式进行特征衍生,然后用逻辑回归进行分类,并画出分类后的效果图。
# -*- coding:utf-8 -*-
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegressionCV
from sklearn import metrics
from sklearn.model_selection import train_test_split
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
def extend(a, b):
return 1.05*a-0.05*b, 1.05*b-0.05*a
if __name__ == '__main__':
pd.set_option('display.width', 200)
data = pd.read_csv('iris.data', header=None)
columns = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'type']
data.rename(columns=dict(zip(np.arange(5), columns)), inplace=True)
data['type'] = pd.Categorical(data['type']).codes
print data.head(5)
x = data.loc[:, columns[:-1]]
y = data['type']
pca = PCA(n_components=2, whiten=True, random_state=0)
x = pca.fit_transform(x)
print '各方向方差:', pca.explained_variance_
print '方差所占比例:', pca.explained_variance_ratio_
print x[:5]
cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
mpl.rcParams['font.sans-serif'] = u'SimHei'
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(facecolor='w')
plt.scatter(x[:, 0], x[:, 1], s=30, c=y, marker='o', cmap=cm_dark)#s表示散点圆圈大小,c表示类别,marker表示标记为圆圈,cmp表示不同类的对比颜色
plt.grid(b=True, ls=':')
plt.xlabel(u'组份1', fontsize=14)
plt.ylabel(u'组份2', fontsize=14)
plt.title(u'鸢尾花数据PCA降维', fontsize=18)
# plt.savefig('1.png')
plt.show()
x, x_test, y, y_test = train_test_split(x, y, train_size=0.7)
model = Pipeline([
('poly', PolynomialFeatures(degree=2, include_bias=True)),
('lr', LogisticRegressionCV(Cs=np.logspace(-3, 4, 8), cv=5, fit_intercept=False))
])
model.fit(x, y)
print '最优参数:', model.get_params('lr')['lr'].C_
y_hat = model.predict(x)
print '训练集精确度:', metrics.accuracy_score(y, y_hat)
y_test_hat = model.predict(x_test)
print '测试集精确度:', metrics.accuracy_score(y_test, y_test_hat)
N, M = 500, 500 # 横纵各采样多少个值
x1_min, x1_max = extend(x[:, 0].min(), x[:, 0].max()) # 第0列的范围
x2_min, x2_max = extend(x[:, 1].min(), x[:, 1].max()) # 第1列的范围
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, M)
x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
x_show = np.stack((x1.flat, x2.flat), axis=1) # 测试点
y_hat = model.predict(x_show) # 预测值
y_hat = y_hat.reshape(x1.shape) # 使之与输入的形状相同
plt.figure(facecolor='w')
plt.pcolormesh(x1, x2, y_hat, cmap=cm_light) # 预测值的显示
plt.scatter(x[:, 0], x[:, 1], s=30, c=y, edgecolors='k', cmap=cm_dark) # 样本的显示
plt.xlabel(u'组份1', fontsize=14)
plt.ylabel(u'组份2', fontsize=14)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.grid(b=True, ls=':')
## 不同类的区域显示不同的颜色
patchs = [mpatches.Patch(color='#77E0A0', label='Iris-setosa'),
mpatches.Patch(color='#FF8080', label='Iris-versicolor'),
mpatches.Patch(color='#A0A0FF', label='Iris-virginica')]
plt.legend(handles=patchs, fancybox=True, framealpha=0.8, loc='lower right')
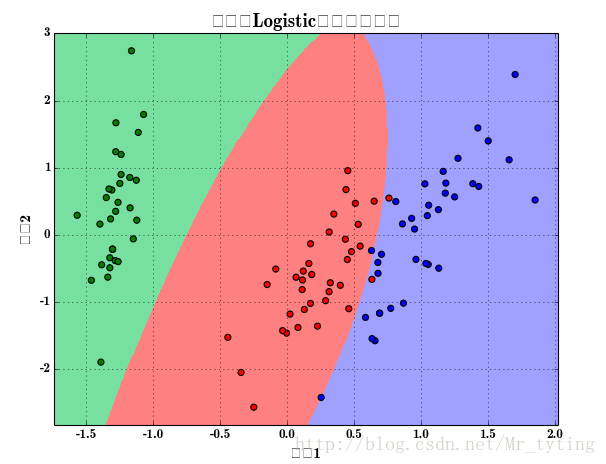
plt.title(u'鸢尾花Logistic回归分类效果', fontsize=17)
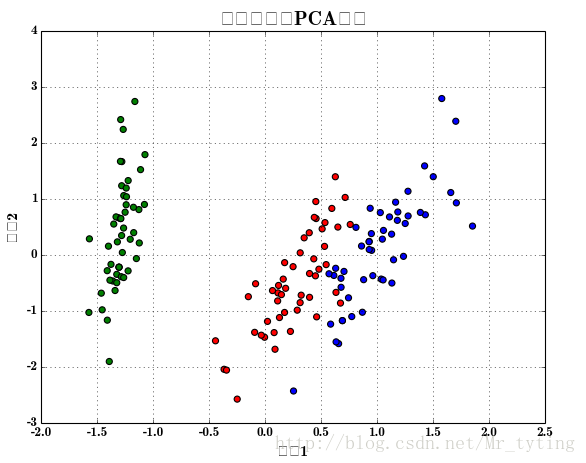
plt.show()样本散点图:
分类后的效果图:
而SVD降维就是对样本特征矩阵进行奇异值分解,来得出最主要的成分。有关SVD降维的更详细内容可以查看我的另外一篇博文机器学习–>矩阵和线性代数里相关内容。
特征选择
关于特征选择的详细内容可以查看我的另外一篇博文sklearn特征选择。
总结
特征抽取,特征选择都能达到降维的效果,那么他们之间有什么区别呢?我个人觉得特征抽取是对所有特征进行了组合,或者说是线性变换,或者说是投影,选择出最好的或者是效果最好的几个投影方向(变换方式),既保证了信息最大程度的保留,又使维度降低了。而特征选择只是单纯的根据某个标准,对特征的重要程度进行了计算,保留最靠前的,最重要的一些特征,剔除剩下的不重要的特征。
无论是特征抽取还是特征选择,都有信息的丢失,但是他们都是丢失一些相对来说不重要的信息,保留他们认为重要的信息。








 本文主要介绍了机器学习中的特征降维方法,包括PCA和SVD降维等特征抽取手段及特征选择方法。通过实例展示了使用PCA降维并结合多项式特征衍生与逻辑回归进行分类的过程。
本文主要介绍了机器学习中的特征降维方法,包括PCA和SVD降维等特征抽取手段及特征选择方法。通过实例展示了使用PCA降维并结合多项式特征衍生与逻辑回归进行分类的过程。
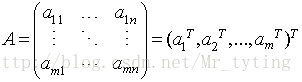

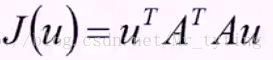
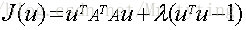
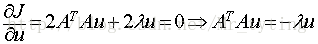

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








