Chapter3 动态规划
动态规划的基本思想
动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合用动态规划法求解的问题,经分解得到的子问题往往不是互相独立的。
- e . g . e.g. e.g.多阶段图最短路问题
下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由 A → E A\to E A→E。求 A → E A\to E A→E的最省费用。
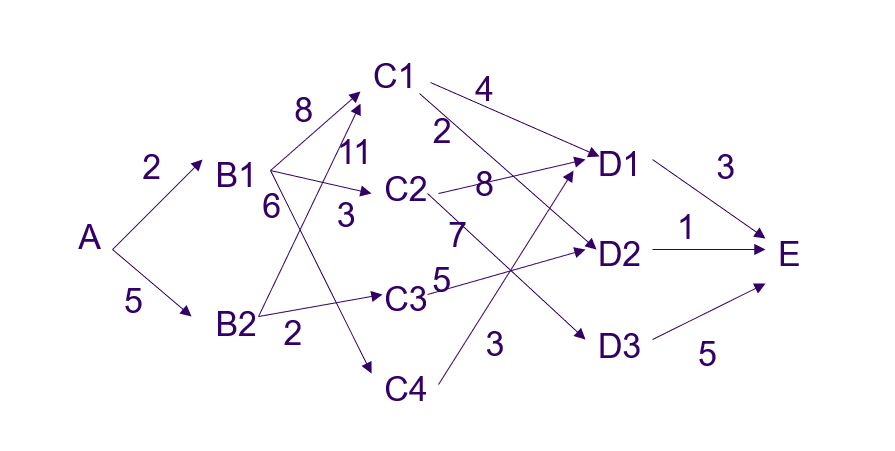
此图有明显的次序,可以划分为5阶段。故此问题的要求是:在各个阶段选取一个恰当的决策,使由这些决策组成的一个决策序列所决定的一条路线,其总路程最短。
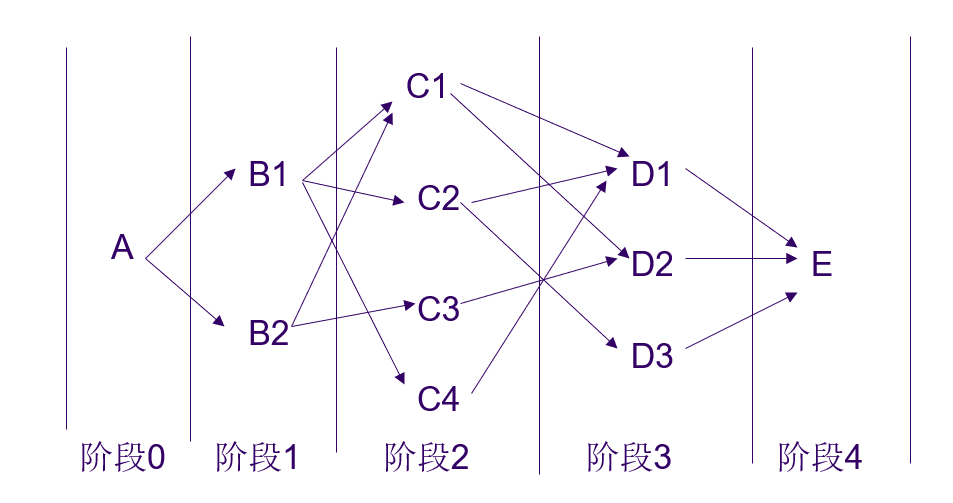
分析:如果 B 1 → E B_1\to E B1→E的最短路已知, B 2 → E B_2\to E B2→E的最短路已知 ⟹ \Longrightarrow ⟹ 知道了最短路
所以,动态规划有以下两个特点
- 原问题的最优解包含了子问题的最优解 ⟶ \longrightarrow ⟶最优子结构
- 求解
B
B
B问题时
- B 1 B_1 B1问题依赖 C 1 , C 2 , C 4 C_1,C_2,C_4 C1,C2,C4的最优解
- B 2 B_2 B2问题依赖 C 1 , C 3 C_1,C_3 C1,C3的最优解
可以看出, C 1 C_1 C1的解被 B 1 , B 2 B_1,B_2 B1,B2重复使用,子问题的解被多次使用 ⟶ \longrightarrow ⟶子问题重叠 ⟶ \longrightarrow ⟶重复计算
设计问题的步骤
- 找出最优解的性质,刻画其结构特征
- 递归的定义最优值
- 以自底向上的方式计算它
- 根据计算最优值时得到的信息,构造最优解
定义递归函数注意要点
- 传的参数,以及它的范围条件
- 递归的边界条件,通常在记忆化搜索中,以记录的元素存在为边界条件
if(Memorized[i][j]) return Memorized[i][j];
- 剪枝的条件
矩阵连乘问题
$Question: $ 给定 n n n个矩阵: A 1 , A 2 , … , A n A_1, A_2, …, A_n A1,A2,…,An,其中 A i A_i Ai与 A i + 1 A_{i+1} Ai+1是可乘的。确定一种连乘的顺序,使得矩阵连乘的计算量为最小。
- 如果直接顺序相乘,矩阵连乘的基本乘法数是
( p × r ) × [ ( p × q ) × q ] (p\times r)\times[(p\times q)\times q] (p×r)×[(p×q)×q]
可以发现,在矩阵很多时,乘法的数目是很庞大的,因此,我们需要最小化乘法的次数来减少计算的时间。
- 不同计算顺序的差别

可以发现:求多个矩阵的连乘积时,计算的结合顺序是十分重要的。
- 考虑一种四个矩阵相乘的特殊情况
设矩阵为 A 1 , A 2 , A 3 , A 4 A_1, A_2, A_3, A_4 A1,A2,A3,A4 , A 1 A_1 A1的行列为 p 0 , p 1 p_0,p_1 p0,p1 A 2 A_2 A2的行列为 p 1 , p 2 . . . p_1,p_2... p1,p2...以此类推.
这样,四个矩阵的行列值,可以通过一个一维数组存放.
int p[5] = {p0,p1,p2,p3,p4};
根据上表的计算顺序对于乘法次数的影响我们可以发现,乘法次数的大小取决于加的括号的位置,于是,我们可以对 A 1 , A 2 , A 3 , A 4 A_1, A_2, A_3, A_4 A1,A2,A3,A4这四个矩阵的乘法顺序进行划分,有以下三种情况
- A 1 , ∣ A 2 , A 3 , A 4 A_1,| A_2, A_3, A_4 A1,∣A2,A3,A4
- A 1 , A 2 , ∣ A 3 , A 4 A_1, A_2, |A_3, A_4 A1,A2,∣A3,A4
- A 1 , A 2 , A 3 , ∣ A 4 A_1, A_2, A_3, |A_4 A1,A2,A3,∣A4
现在要做的工作就是,如果求出了 A 2 , A 3 , A 4 A_2, A_3, A_4 A2,A3,A4, A 1 , A 2 A_1, A_2 A1,A2, A 3 , A 4 A_3, A_4 A3,A4, A 1 , A 2 , A 3 A_1, A_2, A_3 A1,A2,A3这四个子问题的乘法次数的最小值,再把它们三种情况进行比较,就求得了整个问题的最小值.
如果设 m [ i ] [ j ] m[i][j] m[i][j]是矩阵 Π k = i j A i \Pi_{k=i}^{j} A_i Πk=ijAi的值,那么,上述三个的乘法次数如下
- m [ 2 ] [ 4 ] + ( m [ 1 ] [ 1 ] = 0 ) + p 0 p 1 p 4 m[2][4]+(m[1][1]=0)+p_0p_1p_4 m[2][4]+(m[1][1]=0)+p0p1p4
- m [ 1 ] [ 2 ] + m [ 3 ] [ 4 ] + p 0 p 2 p 4 m[1][2]+m[3][4]+p_0p_2p_4 m[1][2]+m[3][4]+p0p2p4
- m [ 1 ] [ 3 ] + ( m [ 4 ] [ 4 ] = 0 ) + p 0 p 3 p 4 m[1][3]+(m[4][4]=0)+p_0p_3p_4 m[1][3]+(m[4][4]=0)+p0p3p4
通过观察,我们可以归纳出从 A i A_i Ai到 A j A_j Aj的通用方程
-
从$A_i 到 到 到A_j$的通用方程
设矩阵 A i A i + 1 . . . A j A_iA_{i+1}...A_j AiAi+1...Aj , k k k是划分的位置
- m [ i ] [ j ] = m i n ( Π k = i j A i ) = m i n i ≤ k < j ( m [ i ] [ k ] + m [ k + 1 ] [ j ] + p i − 1 p k p j ) ( i < j ) m[i][j]=min(\Pi_{k=i}^{j} A_i)=min_{i\le k<j}(m[i][k]+m[k+1][j]+p_{i-1}p_kp_j) (i<j) m[i][j]=min(Πk=ijAi)=mini≤k<j(m[i][k]+m[k+1][j]+pi−1pkpj)(i<j)
- 0 ( i = j ) 0 (i=j) 0(i=j)
备忘录
使用 m [ i ] [ j ] m[i][j] m[i][j]记录已经求过的子问题,避免了相同子问题的重复计算
递归求解
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
const ll maxn = 2e6 + 7;
ll p[maxn];
ll m[1000][1000];
ll recursiveMatrixChain(ll i, ll j) {
if (i == j) return m[i][j]=0;
if (m[i][j] > 0) return m[i][j];
ll minVal = recursiveMatrixChain(i, i) + recursiveMatrixChain(i + 1, j) + p[i - 1] * p[i] * p[j];
m[i][j] = minVal;
for (long long k = i ; k < j; ++k) {
ll tmp = recursiveMatrixChain(i, k) + recursiveMatrixChain(k + 1, j) + p[i - 1] * p[k] * p[j];
if (tmp < minVal) {
minVal = tmp;
}
}
m[i][j] = minVal;
return minVal;
}
int main() {
ll n;
cin >> n;
for (long long i = 0; i <= n; ++i) {
cin >> p[i];
}
int ans=recursiveMatrixChain(1, n);//注意范围,因为题目给定的n是矩阵数目-1所以是n
//如果题目了n个矩阵,那么递归的范围是[1,n-1]
// RecurMatrixChain(1,n);
// for (long long i = 0; i <= n; ++i) {
// for (long long j = 0; j <= n; ++j) {
// cout << m[i][j] << setw(5) << " ";
// }
// cout << '\n';
// }
cout<<ans;
return 0;
}
循环求解
如何避免递归?
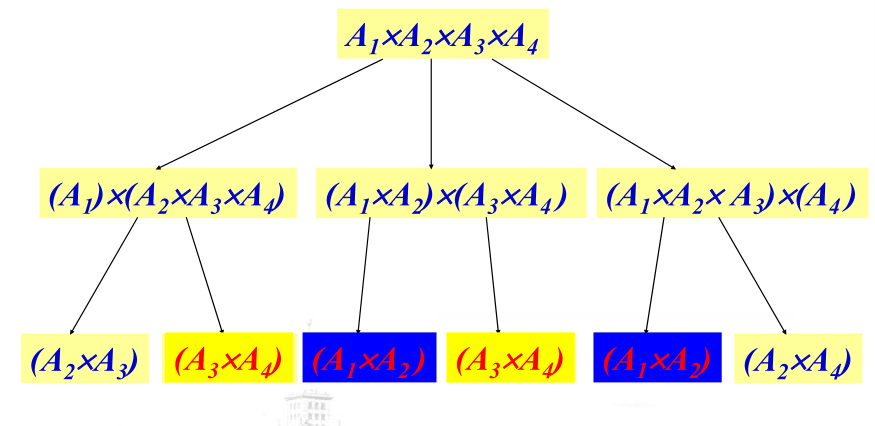
可以发现,递归是自顶向下的求解过程,如果我们换一种思路,从树底求解最小子问题(两个矩阵连乘的问题),再用求解好的子问题求解更上层的问题,最终达到求解1-n整个问题答案的目的
时间复杂度为: O ( n 3 ) O(n^3) O(n3)
空间复杂度为: O ( n 2 ) O(n^2) O(n2)
- Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
const ll maxn = 2e6 + 7;
int m[2000][2000];
int p[2000];
int s[2000][2000];
int n;
int matrixChain() {
for (long long i = 0; i <= n; ++i) {
//对角线上的元素置0
m[i][i] = 0;
}
for (long long i = n; i >= 1; --i) {
for (long long j = i + 1; j <= n; ++j) {
//找出每一个的初值
m[i][j] = m[i][j] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (long long k = i + 2; k < j; ++k) {//i+1已经比过
//找到最小值
int tmp = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (tmp < m[i][j]) {
m[i][j] = tmp;
s[i][j] = k;
}
}
}
}
return m[1][n];
}
void trace(int i, int j) {
if (i == j) {
cout << 'A' << i;
return;
}
cout << "(";
int k = s[i][j];
trace(i, k);
trace(k + 1, j);
cout << ")";
return;
}
int main() {
cin >> n;
for (long long i = 0; i <= n; ++i) {
cin >> p[i];
}
cout << matrixChain() << endl;
trace(1, n);
cout << endl;
for (long long i = 0; i <= n; ++i) {
for (long long j = 0; j <= n; ++j) {
cout << m[i][j] << ' ';
}
cout << '\n';
}
return 0;
}
路径问题
问题集
- 数字三角形
https://www.luogu.com.cn/problem/P1216
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
const ll maxn = 2e6 + 7;
int dp[1001][1001];
int main() {
ll n;
cin >> n;
for (long long i = 0; i <= n; ++i) {
for (long long j = 0; j <= n; ++j) {
dp[i][j] = -1000000;
}
}
for (long long i = 1; i <= n; ++i) {
for (long long j = 1; j <= i; ++j) {
cin >> dp[i][j];
}
}
for (long long i = n - 1; i >= 1; --i) {
for (long long j = 1; j <= i; ++j) {
dp[i][j] += max(dp[i + 1][j], dp[i + 1][j + 1]);
}
}
// for (long long i = 0; i <= n; ++i) {
// for (long long j = 0; j <= n; ++j) {
// cout << dp[i][j] << ' ';
// }
// cout << endl;
// }
cout << dp[1][1];
return 0;
}
- 滑雪
https://www.luogu.com.cn/problem/P1434
记忆化DFS
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
const ll maxn = 2e6 + 7;
ll dx[4] = {1, -1, 0, 0};
ll dy[4] = {0, 0, 1, -1};
ll a[1001][1001];
ll s[1001][1001];
ll r, c;
ll dfs(ll x, ll y) {
if (s[x][y]) return s[x][y];
s[x][y] = 1;
for (long long i = 0; i < 4; ++i) {
ll xi = x + dx[i];
ll yi = y + dy[i];
if (xi > 0 && yi > 0 && xi <= r && yi <= c && a[x][y] > a[xi][yi]) {
//这里的边界有效条件除了考虑xi,yi的不能超范围,还要保证已经搜过的不能再搜的边界条件,也就是a[x][y] > a[xi][yi]
dfs(xi, yi);
s[x][y] = max(s[x][y], s[xi][yi] + 1);
}
}
return s[x][y];
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> r >> c;
for (long long i = 1; i <= r; ++i) {
for (long long j = 1; j <= c; ++j) {
cin >> a[i][j];
}
}
ll ans = -1;
for (long long i = 1; i <= r; ++i) {
for (long long j = 1; j <= c; ++j) {
ans = max(ans, dfs(i, j));
}
}
cout << ans << endl;
// for (long long i = 0; i <= r; ++i) {
// for (long long j = 0; j <= c; ++j) {
// cout << s[i][j] << ' ';
// }
// cout << endl;
// }
return 0;
}
最长公共子序列(LCS)
Q u e s t i o n Question Question
若给定序列 X = x 1 , x 2 , … , x m X={x_1,x_2,…,x_m} X=x1,x2,…,xm,则另一序列 Z = z 1 , z 2 , … , z k Z={z_1,z_2,…,z_k} Z=z1,z2,…,zk,是 X X X的子序列是指存在一个严格递增下标序列 i 1 , i 2 , … , i k {i_1,i_2,…,i_k} i1,i2,…,ik使得对于所有 j = 1 , 2 , … , k j=1,2,…,k j=1,2,…,k有: z j = x i j z_j=x_{ij} zj=xij。
例如,序列 Z = B , C , D , B Z={B,C,D,B} Z=B,C,D,B是序列 X = A , B , C , B , D , A , B X={A,B,C,B,D,A,B} X=A,B,C,B,D,A,B的子序列,相应的递增下标序列为 2 , 3 , 5 , 7 {2,3,5,7} 2,3,5,7。
给定 2 2 2个序列 X X X和 Y Y Y,当另一序列 Z Z Z既是 X X X的子序列又是 Y Y Y的子序列时,称 Z Z Z是序列 X X X和 Y Y Y的公共子序列。
给定 2 2 2个序列 X = x 1 , x 2 , … , x m X={x_1,x_2,…,x_m} X=x1,x2,…,xm和 Y = y 1 , y 2 , … , y n Y={y_1,y_2,…,y_n} Y=y1,y2,…,yn,找出 X X X和 Y Y Y的最长公共子序列。
- LCS的结构分析
设序列
X
=
x
1
,
x
2
,
…
,
x
m
X={x_1,x_2,…,x_m}
X=x1,x2,…,xm和的
Y
=
y
1
,
y
2
,
…
,
y
n
Y={y_1,y_2,…,y_n}
Y=y1,y2,…,yn最长公共子序列为
Z
=
z
1
,
z
2
,
…
,
z
k
Z={z_1,z_2,…,z_k}
Z=z1,z2,…,zk ,则
(1)若
x
m
=
y
n
x_m=y_n
xm=yn,则
z
k
=
x
m
=
y
n
z_k=x_m=y_n
zk=xm=yn,且
Z
k
−
1
Z_{k-1}
Zk−1是
X
m
−
1
X_{m-1}
Xm−1和
Y
n
−
1
Y_{n-1}
Yn−1的最长公共子序列。
(2)若
x
m
≠
y
n
x_m≠y_n
xm=yn且
z
k
≠
x
m
z_k≠x_m
zk=xm,则
Z
Z
Z是
X
m
−
1
X_{m-1}
Xm−1和
Y
Y
Y的最长公共子序列。
(3)若
x
m
≠
y
n
x_m≠y_n
xm=yn且
z
k
≠
y
n
z_k≠y_n
zk=yn,则
Z
Z
Z是
X
X
X和
Y
n
−
1
Y_{n-1}
Yn−1的最长公共子序列。
由此可见,2个序列的最长公共子序列包含了这2个序列的前缀的最长公共子序列。因此,最长公共子序列具有最优子结构性质(2,3条件下总有一个最优解)。
由LCS 的最优子结构性质建立子问题最优值的递归关系。用 c [ i ] [ j ] c[i][j] c[i][j]记录序列 X i X_i Xi和 Y j Y_j Yj的最长公共子序列的长度。其中, X i = x 1 , x 2 , … , x i X_i={x_1,x_2,…,x_i} Xi=x1,x2,…,xi; Y j = y 1 , y 2 , … , y j Y_j={y_1,y_2,…,y_j} Yj=y1,y2,…,yj。当 i = 0 i=0 i=0或 j = 0 j=0 j=0时,空序列是 X i X_i Xi和 Y j Y_j Yj的最长公共子序列。故此时 c [ i ] [ j ] = 0 c[i][j]=0 c[i][j]=0。其它情况下,由最优子结构性质可建立递归关系如下:
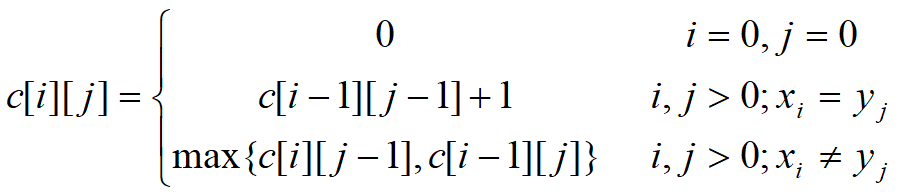
可以发现
- 这是一个二维表
- 填表顺序从左上角到右下角
- 时间复杂度和空间复杂度都为 O ( n 2 ) O(n^2) O(n2)
同时LCS还具有子问题的重叠性
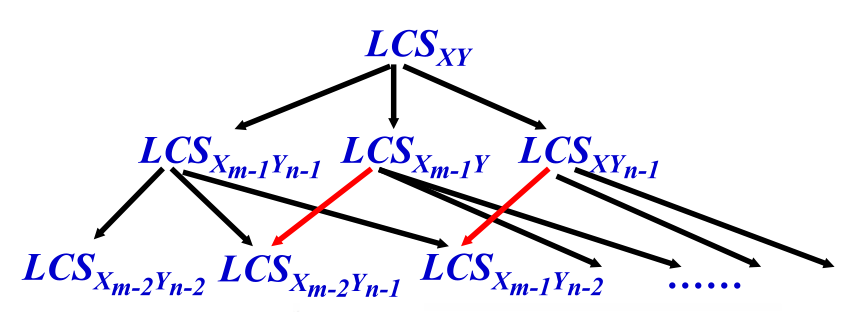
- 算法思路
自左而右自上而下建立表格
m
a
t
r
i
x
matrix
matrix[][]。
(1)如果
s
t
r
1
[
i
]
=
s
t
r
2
[
j
]
str1[i]=str2[j]
str1[i]=str2[j]则将左上角元素值加1赋值给
m
a
t
r
i
x
[
i
]
[
j
]
matrix[i][j]
matrix[i][j],如果本身是最左上角元素就为1。
(2)如果
s
t
r
1
[
i
]
str1[i]
str1[i]不等于
s
t
r
2
[
j
]
str2[j]
str2[j]则该点元素值取
m
a
t
r
i
x
[
i
-
1
]
[
j
]
matrix[i-1][j]
matrix[i-1][j]和
m
a
t
r
i
x
[
i
]
[
j
-
1
]
matrix[i][j-1]
matrix[i][j-1]中较大的一个。如果
i
=
0
i=0
i=0且
j
=
0
j=0
j=0(最左上角)则取
0
0
0。
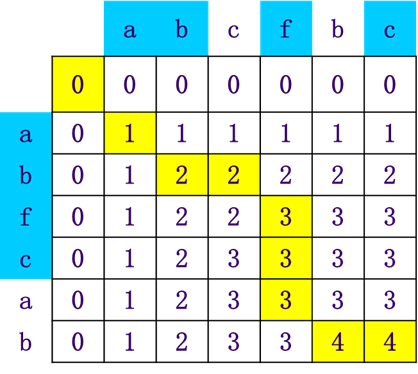
- Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
const ll maxn = 2e6 + 7;
int c[2000][2000];
void LCSLength(char x[], char y[]) { //调用该函数前,先将c数组置初值为0
int i, j;
for (i = 1; i <= strlen(x); i++) //自上而下
for (j = 1; j <= strlen(y); j++) { //每行自左向右
if (x[i - 1] == y[j - 1])//下标从0开始
c[i][j] = c[i - 1][j - 1] + 1;
else if (c[i - 1][j] >= c[i][j - 1]) {
c[i][j] = c[i - 1][j];
} else c[i][j] = c[i][j - 1];
}
}
void LCS(int i, int j, char x[], char y[]) {
if (i == 0 || j == 0) {
return;
}
if (x[i - 1] == y[j - 1]) {//下标从0开始
LCS(i - 1, j - 1, x, y);
cout << x[i - 1];//下标从0开始
} else if (c[i - 1][j] >= c[i][j - 1]) {
LCS(i - 1, j, x, y);
} else LCS(i, j - 1, x, y);
}
char x[12000];
char y[12000];
int main() {
cin >> x >> y;
LCSLength(x, y);
int lenx = strlen(x);
int leny = strlen(y);
cout << c[lenx][leny] << endl;
for (long long i = 0; i <= max(lenx, leny); ++i) {
for (long long j = 0; j <= max(lenx, leny); ++j) {
cout << c[i][j] << ' ';
}
cout << endl;
}
LCS(lenx, leny, x, y);
return 0;
}
/*
dabcfbc eabfcab
*/






















 618
618











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








