线性代数学习笔记之矩阵

C_TA说

已于 2024-12-20 22:50:15 修改

阅读量4.9k

点赞数 26

分类专栏： # 线性代数文章标签：线性代数学习笔记

于 2024-11-28 16:37:48 首次发布

本文链接：https://blog.csdn.net/My_Champion/article/details/143893849

版权

线性代数专栏收录该内容

7 篇文章

订阅专栏

1. 矩阵的基础知识

1.1 矩阵的概念

（1）矩阵：由 $m$ X $n$ 个数排成一个 $m$ 行 $n$ 列的数表，称为一个 $m$ X $n$ 矩阵。

$eg:A= \begin{pmatrix} a_{11} & a_{12} & ... &a_{1n} \\ a_{21} & a_{22} &... &a_{2n} \\ ...& ... &... & ...\\ a_{m1} &a_{m2} & ... & a_{mn} \end{pmatrix}$

备注：

1. 矩阵中某元素用 $a_{ij}$ 表示，代表第 $i$ 行，第 $j$ 列的元素。

2. 记作： $A=(a_{ij})_{m*n}$ 。

（2）同型矩阵：矩阵A的行数和列数与矩阵B的行数和列数相等，则称这两个矩阵为同型矩阵。

备注：矩阵A与矩阵B是同型矩阵 $\Leftrightarrow$ 矩阵A与矩阵B的行数相等，列数相等。

（3）相等矩阵：矩阵A的行数和列数与矩阵B的行数和列数相等，同时对应位置的元素也相等，则

称这两个矩阵为相等矩阵。

备注：

1. 矩阵A与矩阵B是相等矩阵 $\Leftrightarrow$ A=B $\Leftrightarrow$ 矩阵A与矩阵B的行数相等，列数相等，对应位置的元素相等。

2. 相等矩阵属于同型矩阵。

（4）几类特殊的矩阵：

1）列矩阵：只有一列的矩阵，又称为列向量。

$eg:A=\begin{pmatrix} a\\ b\\ c \end{pmatrix}$ $\beta =\begin{pmatrix} a\\ b\\ c \end{pmatrix}$

2）行矩阵：只有一行的矩阵，又称为行向量。

$eg:A=\begin{pmatrix} a& b& c\\ \end{pmatrix}$ $\alpha =\begin{pmatrix} a,& b, &c \end{pmatrix}$

3）零矩阵：元素全为0的矩阵，记作 $O$ 。

$eg:O=\begin{pmatrix} 0 &0 \\ 0& 0 \end{pmatrix}$ $O=\begin{pmatrix} 0 & 0&0 \\ 0 & 0 & 0 \end{pmatrix}$

4）方阵：顾名思义，方方正正，即行数与列数相等的矩阵。

备注：

1. 从外观上看就是把行列式的|...|换成[...]或(...)。

2. 方阵若是 $n$ 行 $n$ 列的，则称为 $n$ 阶方阵。

3. 方阵具备主对角线和副对角线的定义，非方阵的矩阵不具备此定义。

4. 一阶方阵： $(a)=a$ ，就是一个数。

45）上三角矩阵：主对角线下方的元素全为0的方阵。

46）下三角矩阵：主对角线上方的元素全为0的方阵。

47）对角矩阵：主对角线上方、下方的元素全为0的方阵。

$eg:A=\begin{pmatrix} a_{1} & & & \\ & a_{2} & & \\ & &... & \\ & & & a_{n} \end{pmatrix}\Leftrightarrow diag(a_{1},a_{2},...,a_{n})$

478）数量矩阵：主对角线上的元素都是同一个常数的对角矩阵，又称 $n$ 阶数量矩阵。

$eg:A=\begin{pmatrix} a & & & \\ & a & & \\ & &... & \\ & & & a\end{pmatrix}$

4789）单位矩阵：主对角线上的元素都是1的对角矩阵，又称 $n$ 阶单位矩阵，记作 $E$ 或 $I$ 。

$eg:A=\begin{pmatrix} 1 & & & \\ & 1 & & \\ & &... & \\ & & & 1\end{pmatrix}$

备注：

1. 上述矩阵中空白的部分都是0。

2. 单位矩阵除主对角线外的元素都是0，所有元素都是 1 的矩阵不是单位矩阵。

小贴士：矩阵与行列式的区别

1.2 矩阵的运算

（1）矩阵的加减法

遵守原则：1）相加减的两个矩阵为同型矩阵；2）对应位置元素相加减。

$eg:\begin{pmatrix} a_{1}&b_{1} \\ a_{2}& b_{2} \\ a_{3}& b_{3} \end{pmatrix}\pm \begin{pmatrix} c_{1}&d_{1} \\ c_{2}& d_{2} \\ c_{3}& d_{3} \end{pmatrix}=\begin{pmatrix} a_{1}\pm c_{1}& b_{1}\pm d_{1}\\ a_{2}\pm c_{2}&b_{2}\pm d_{2} \\ a_{3}\pm c_{3}& b_{3}\pm d_{3} \end{pmatrix}$

备注：

1. A + B = B + A 交换律

2. (A + B) + C = A + (B + C) 结合律

3. A + B = C $\Leftrightarrow$ A = C - B 移项

4. A + $O$ = A 零矩阵 $O$ 与A为同型矩阵

5. A - A = $O$ 零矩阵 $O$ 与A为同型矩阵

（2）矩阵的数乘

遵守原则：用数 $k$ 乘以矩阵A，就是用数 $k$ 乘以矩阵A内的每一个元素。

$eg:k*\begin{pmatrix} a& b&c \\ u& v& w\\ x& y& z \end{pmatrix}=\begin{pmatrix} k*a& k* b&k*c \\ k*u& k* v& k*w\\ k* x&k* y& k*z \end{pmatrix}$

备注：

1. $k$ (A + B) = $k$ A + $k$ B 2. ( $k$ + $l$ )A = $k$ A + $l$ A

3. $k$ ( $l$ A) = $l$ ( $k$ A) = ( $k$ $l$ )A 其中： $k$ 、 $l$ 为常数

小贴士：

1. 矩阵的所有元素都有公因子 $k$ ，则 $k$ 外提一次；

2. 行列式的某一行（列）有公因子 $k$ ，则 $k$ 外提一次；

3. 行列式的所有元素都有公因子 $k$ ，则 $k$ 外提 $n$ 次；

（3）矩阵的乘法

遵守原则：1）矩阵A的列数与矩阵B的行数必须相等；

2）矩阵C的行数是矩阵A的行数，矩阵C的列数是矩阵B的列数；

3）矩阵A的每行元素分别乘以矩阵B的每列元素，再做和，结果写到相应的行列坐标

位置上。

$eg:A = \begin{pmatrix} a & b\\ c &d \\ e & f \end{pmatrix}$ 3 x 2 $B = \begin{pmatrix} u & v& w & p\\ x& y& z& q \end{pmatrix}$ 2 x 4

$C=A*B=\begin{pmatrix} au+bx& av+by& aw+bz& ap+bq\\ cu+dx& cv+dy& cw+dz& cp+dq\\ eu+fx& ev+fy& ew+fz& ep+fq\\ \end{pmatrix}$ 3 x 4

备注1：

1. 矩阵的乘法不满足交换律，即是区分左乘和右乘的。

2. 矩阵的乘法不满足消去律。

3. 两个非零矩阵的乘积可能是零矩阵。

4. 两个矩阵的乘积可能是零矩阵，也可能是0。

备注2：

1. （AB）C = A（BC）结合律（顺序不能变）

2. （A+B）C = AC + BC ; C（A+B） = CA + CB 分配律（顺序不能变）

3. $k$ （AB）= （ $k$ A）B = A（ $k$ B）（顺序不能变）

4. A $E_{1}$ = A； $E_{2}$ A = A. ( $E_{1}$ 与 $E_{2}$ 可能是不同阶的单位矩阵）

5. 数量矩阵A = diag(a,a,...a) = aE，则有AB = aEB = aB.

（4）矩阵的可交换性

判定条件：矩阵A与矩阵B可交换 $\Leftrightarrow$ 矩阵A与矩阵B是同阶方阵，且AB=BA。

1.3 方阵的幂

（1）定义：矩阵A为方阵， $k$ 为正整数，则矩阵A的 $k$ 次幂为 $A^{k}=A*A*...*A$ 。

备注：

1. 矩阵只有是方阵的时候，才具备幂的概念。

2. $A^{0}= E$ 。

（2）性质：

1） $A^{k_{1}}*A^{k_{2}}=A^{k_{1}+k_{2}}$ (A为方阵， $k_{1},k_{2}$ 为非负整数)

2） $(A^{k_{1}})^{k_{2}}=A^{k_{1}*k_{2}}$ (A为方阵， $k_{1},k_{2}$ 为非负整数)

3） $(lA)^{k}= l^{k}*A^{k}$ (A为方阵， $l$ 为常数， $k$ 为正整数)

4）方阵多项式：

5）若矩阵A和矩阵B为同阶方阵，则有：

① $A^{2}-E^{2}=(A+E)(A-E)=(A-E)(A+E)$

② $(A\pm E)^{2}=A^{2}\pm 2AE+E^{2}$

③ $A^{3}-E^{3}= (A-E)(A^{2}+AE+E^{2})$

④ $A^{3}+E^{3}= (A+E)(A^{2}-AE+E^{2})$

⑤ $(A*E)^{k}= A^k*E^{k}$

6）若矩阵A和矩阵B可交换，则有：

① $A^{2}-B^{2}=(A+B)(A-B)=(A-B)(A+B)$

② $(A\pm B)^{2}=A^{2}\pm 2AB+B^{2}$

③ $A^{3}-B^{3}= (A-B)(A^{2}+AB+B^{2})$

④ $A^{3}+B^{3}= (A+B)(A^{2}-AB+B^{2})$

⑤ $(A*B)^{k}= A^k*B^{k}$

小贴士：

1. 求解矩阵的幂时，可先求2到3次矩阵的幂，然后找其规律求解。

2. 求解矩阵的幂时，可对目标矩阵进行反向构造，构造成由行矩阵和列矩阵乘积的形式，再

利用矩阵的幂的定义求解。

1.4 矩阵的转置

（1）定义：将矩阵A的行列对换，得到的新矩阵即为矩阵A的转置，可记作 $A^{T}$ 。

（2）性质：

1） $(A^{T})^{T}=A$ 2） $(A \pm B)^{T}=A^{T}\pm B^{T}$

3） $(kA)^{T}=kA^{T}$ ， $k$ 为常数。 4） $(ABC)^{T}=C^{T}B^{T}A^{T}$

5） $(A^{m})^{T}=(A^{T})^{m}$ ， $m$ 为正整数。

（3）对称矩阵[方阵]

1）定义：若矩阵A满足 $A^{T}=A$ ，则称矩阵A为对称矩阵。

2）特性：

① $A=(a_{ij})_{m*n}$ 为对称矩阵 $\Leftrightarrow$ $A^{T}=A$ $\Leftrightarrow$ $a_{ij}=a_{ji}$

② 对称矩阵的主对角线元素为任意数。

③ 对称矩阵，以主对角线为轴，上下对应元素相等。

备注：

1. 若矩阵A和矩阵B是同阶的对称矩阵，则A±B仍为对称矩阵。

2. 若矩阵A是对称矩阵，则 $kA$ , $A^{m}$ 仍为对称矩阵。其中： $k$ 为常数， $m$ 为正整数。

3. 若矩阵A和矩阵B是同阶的对称矩阵，则矩阵AB为对称矩阵的充要条件是AB=BA。

4. 对于任意 $m$ X $n$ 矩阵A，则 $A^{T}A$ ， $AA^{T}$ 均为对称矩阵。

（4）反对称矩阵[方阵]

1）定义：若矩阵A满足 $A^{T}=-A$ ，则称矩阵A为反对称矩阵。

2）特性：

① $A=(a_{ij})_{m*n}$ 为反对称矩阵 $\Leftrightarrow$ $A^{T}=-A$ $\Leftrightarrow$ $a_{ij}=-a_{ji}$

② 反对称矩阵的主对角线元素全为0。

③ 反对称矩阵，以主对角线为轴，上下对应元素互为相反数。

备注：

1. 若矩阵A和矩阵B是同阶的反对称矩阵，则A±B仍为反对称矩阵。

2. 若矩阵A是反对称矩阵，则 $kA$ 仍为反对称矩阵。其中： $k$ 为常数，下边的 $m$ 为正整数。

3. 若矩阵A是反对称矩阵，则 $A^{m}$ 【当 $m$ 为奇数时为反对称矩阵；当 $m$ 为偶数时为对称矩阵】。

1.5 方阵的行列式

（1）定义：设 $n$ 阶方阵A为: ↓↓↓↓↓↓ 则 $n$ 阶方阵A的行列式为：↓↓↓↓

$A= \begin{pmatrix} a_{11} & a_{12} & ... &a_{1n} \\ a_{21} & a_{22} &... &a_{2n} \\ ...& ... &... & ...\\ a_{n1} &a_{n2} & ... & a_{nn} \end{pmatrix}$ ， $|A|= \begin{vmatrix} a_{11} & a_{12} & ... &a_{1n} \\ a_{21} & a_{22} &... &a_{2n} \\ ...& ... &... & ...\\ a_{n1} &a_{n2} & ... & a_{nn} \end{vmatrix}$ .

备注：

1. 只有当矩阵是方阵的时候，才有行列式。

2. 方阵A的行列式|A|是一个数。

3. 方阵具备诸多属性，行列式只是其中属性之一。

（2）性质：若矩阵A和矩阵B是同阶方阵， $k$ 为常数， $m$ 为正整数，则有：

1） $\left | A^{T} \right |=\left | A \right |$ 2） $\left |k A \right |=k^{n}\left | A \right |$

3） $\left | AB \right |=\left | A \right |\left | B \right |$ 4） $\left | A^{m} \right |=\left | A \right |^{m}$

5） $\left | E \right |=1$ ， $E$ 为单位矩阵。

1.6 方阵的伴随矩阵

（1）定义：设矩阵A为 $n$ 阶方阵，将 $\left | A \right |$ 中的每个元素替换成对应的代数余子式，然后再转置，所

形成的新的矩阵，即为矩阵A的伴随矩阵(非原定义)，记作 $A^{*}$ ，表示如下：

$A^{*}=\begin{pmatrix} A_{11} & A_{21} & ... & A_{n1} \\ A_{12}& A_{22} & ... &A_{n2} \\ ...& ... & ... & ...\\ A_{1n}& A_{2n} &... & A_{nn} \end{pmatrix}$ .

备注：

1. 只有当矩阵是方阵的时候，才有伴随矩阵。

2. 任意方阵都有伴随矩阵。

3. 按行求，按列放。

（2）性质：

1） $AA^{*}=A^{*}A=\left | A \right |E$ 2） $\left | A^{*} \right |=\left | A \right |^{n-1}$

3） $(A^{T})^{*}=(A^{*})^{T}$ 4） $(kA)^{*}=k^{n-1}A^{*}$ , $k$ 为常数。

5）若 $A=\begin{pmatrix} a & b\\ c& d \end{pmatrix}$ ，则 $A^{*}=\begin{pmatrix} d & -b\\ -c & a \end{pmatrix}$ ,即主对角线元素互换，副对角线元素变号。

1.7 方阵的逆矩阵

（1）定义：设矩阵A为 $n$ 阶方阵，若存在 $n$ 阶方阵B，使得 $AB=BA=E$ ，则称矩阵A是可逆矩

阵，记作 $A^{-1}$ ,矩阵B为矩阵A的逆矩阵，即 $A^{-1}=B$ 。

备注：

1. 矩阵只有是方阵的时候，才能讨论矩阵的可逆性。

2. 不是所有的方阵都有逆矩阵，故方阵分为可逆矩阵和不可逆矩阵，二者必居其一。

3. 若方阵A是可逆矩阵，那么它的逆矩阵是唯一的。

（2）推论：设矩阵A为 $n$ 阶方阵，若存在 $n$ 阶方阵B，使得 $AB=E$ 或 $BA=E$ ，则称矩阵A是可

逆矩阵，记作 $A^{-1}$ ,矩阵B为矩阵A的逆矩阵，即 $A^{-1}=B$ 。

（3）矩阵可逆的判定及逆矩阵的求法：

1）矩阵可逆的判定方法：方阵A可逆的充分必要条件是 $\left | A \right |\neq 0$ 。

备注：

1. 充分性证明： $AA^{*} =A^{*}A=\left | A \right |E$ （同除行列式|A|）

2. 必要性证明： $AA^{-1}=A^{-1}A=E$ （同取行列式）

2）逆矩阵求法： $A^{-1}=\frac{A^{*}}{\left | A \right |}$ （伴随矩阵法）

备注：

1. 对角矩阵A可逆的充分必要条件是主对角线的每个元素都不为0，且 $A^{-1}$ 为主对角线元素取倒数。

2. 只有明确矩阵A是可逆的，才允许使用 $A^{-1}$ 。

（4）性质：

1）若方阵A可逆，则逆矩阵 $A^{-1}$ 也可逆，且 $(A^{-1})^{-1}=A$ 。

2）若方阵A可逆，则 $A^{T}$ 也可逆，且 $(A^{T})^{-1}=(A^{-1})^{T}$ 。

3）若方阵A可逆， $k$ 为非零常数，则 $kA$ 也可逆，且 $(kA)^{-1}=\frac{1}{k}A^{-1}$ 。

4）若方阵A可逆，则 $A^{*}$ 也可逆，且 $(A^{*})^{-1} = (A^{-1})^{*}=\frac{A}{\left | A \right |}$ 。

5）若矩阵A，B为同阶可逆方阵，则AB也可逆，且 $(AB)^{-1}=B^{-1}A^{-1}$ 。

6）若方阵A可逆， $m$ 为正整数，则 $A^{m}$ 也可逆，且 $(A^{m})^{-1}= (A^{-1})^{m}$ 。

7）若方阵A可逆，则 $\left | A^{-1} \right |=\frac{1}{\left | A \right |}$ 。

1.8 方阵的矩阵方程

若矩阵A和矩阵B都是可逆矩阵，则矩阵方程：

（1）AX = C，其解为：X = $A^{-1}C$ 。

（2）XA = C，其解为：X = $CA^{-1}$ 。

（3）AXB = C，其解为：X = $A^{-1}CB^{-1}$ 。

备注：

1. 永远不要把矩阵放分母上。

2. 矩阵永远不会和常量运算，要引入单位矩阵进行辅助。

2. 矩阵的初等变换

（1）矩阵的初等变换：分为初等行变换和初等列变换。

遵循原则：①：交换矩阵的两行（列）。 $\rightarrow$ 第一类初等变换

②：用数 $k$ ≠ 0乘以矩阵某一行（列）的所有元素。 $\rightarrow$ 第二类初等变换

③：把矩阵某一行（列）所有元素的 $l$ 倍加到另一行（列）对应的元素上。

$\rightarrow$ 第三类初等变换

备注：矩阵进行初等变换时，矩阵间用箭头表示，不能用等号，且变换过程要注明清楚。

（2）矩阵的标准形：

要求：①：矩阵内元素只包含0和1。

②：矩阵的左上角是一个单位矩阵，其余元素皆为0。

$eg1:\begin{pmatrix} 1 & 0\\ 0 & 0 \end{pmatrix}$ $eg2:\begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}$

$eg3:\begin{pmatrix} 1&0 \\ 0& 1\\ 0& 0 \end{pmatrix}$ $eg4:\begin{pmatrix} 1& 0 &0 & 0\\ 0&1 & 0 &0 \\ 0&0 & 1 & 0 \end{pmatrix}$

备注：矩阵化标准形矩阵时，遵循矩阵的初等变换原则。

（3）行阶梯形矩阵：

要求：①：如果矩阵存在零行，则零行都在非零行下面。

②：每个非零行，的第一个非零元素，的左下方全为零。

备注：

1. 矩阵化行阶梯形矩阵时，遵循矩阵的初等行变换原则。

2. 绘制阶梯线时，一次只能下一个台阶，而台阶面部分允许宽窄不等。

$eg:\begin{pmatrix} 5 & 6& 1 & 0 &1 \\ 0& 2& 2& 7 &6 \\ 0& 0& 0& 0 &3 \\ 0& 0& 0& 0 &0 \end{pmatrix}$

（3）行简化阶梯形矩阵：

要求：①：必须是行阶梯形矩阵。

②：每个非零行，的第一个非零元素，必须是1。

③：每个非零行，的第一个非零元素，所在列的其他元素都为0。

备注：

1. 矩阵化行简化阶梯形矩阵时，遵循矩阵的初等行变换原则。

2. 绘制阶梯线时，一次只能下一个台阶，而台阶面部分允许宽窄不等。

$eg:\begin{pmatrix} 1 & 0& 1 & 3 &0 \\ 0& 1& 2& 4 &0 \\ 0& 0& 0& 0 &1 \\ 0& 0& 0& 0 &0 \end{pmatrix}$

小贴士：

1. 任何矩阵通过初等行变换都能化成行阶梯形矩阵，行阶梯形矩阵是不唯一的。

2. 任何矩阵通过初等行变换都能化成行简化阶梯形矩阵，行简化阶梯形矩阵是唯一的。

3. 单位矩阵的初等矩阵

（1）定义：由单位矩阵经过一次的初等变换所得到的矩阵，称为初等矩阵。 $\Rightarrow$ 初等矩阵为方阵。

（2）类型：

1）第一类初等矩阵：交换单位矩阵的第 $i,j$ 两行（列）所得到的初等矩阵。

$eg:\begin{pmatrix} 1 & & \\ & 1 & \\ & & 1 \end{pmatrix}\rightarrow \begin{pmatrix} & 1 & \\ 1 & & \\ & & 1 \end{pmatrix}$

2）第二类初等矩阵：用非零数 $k$ 乘以单位矩阵的第 $i$ 行（列）所得到的初等矩阵。

$eg:\begin{pmatrix} 1 & & \\ & 1& \\ & & 1 \end{pmatrix}\rightarrow \begin{pmatrix} 1 & & \\ & 1& \\ & & 6 \end{pmatrix}$

3）第三类初等矩阵：把单位矩阵的第 $j$ 行（列）的 $l$ 倍加到第 $i$ 行（列）所得到的初等矩阵。

$eg:\begin{pmatrix} 1 & & \\ & 1& \\ & & 1 \end{pmatrix}\rightarrow \begin{pmatrix} 1 & & \\ & 1& \\ 8 & & 1 \end{pmatrix}$ $eg:\begin{pmatrix} 1 & & \\ & 1& \\ & & 1 \end{pmatrix}\rightarrow \begin{pmatrix} 1 & &8 \\ & 1& \\ & & 1 \end{pmatrix}$

（3）性质：

1）初等矩阵的行列式都不为0。 $\Rightarrow$ 初等矩阵均可逆。

2）初等矩阵的转置矩阵，仍为同种类型的初等矩阵。

备注：①： $E(ij)^{T} = E(ij)$ ②： $E(i(k))^{T} = E(i(k))$ ③： $E(ij(l))^{T} = E(ji(l))$

同种类型的初等矩阵指单位矩阵通过第一类、第二类、第三类初等变换得到的初等矩阵。

3）初等矩阵的逆矩阵，仍为同种类型的初等矩阵。

备注：①： $E(ij)^{-1} = E(ij)$ ②： $E(i(k))^{-1} = E(i(\frac{1}{k})$ ③： $E(ij(l))^{-1} = E(ij(-l))$

同种类型的初等矩阵指单位矩阵通过第一类、第二类、第三类初等变换得到的初等矩阵。

小贴士：初等矩阵与矩阵的初等变换的关系

设矩阵A为 $m$ X $n$ 矩阵，则：

①：对矩阵A进行一次初等行变换得到的矩阵B，等于用同种类型的 $m$ 阶初等矩阵左乘A，即PA = B。

②：对矩阵A进行一次初等列变换得到的矩阵B，等于用同种类型的 $n$ 阶初等矩阵右乘A，即AP = B。

注：P为单位矩阵通过第一类、第二类、第三类初等变换得到的初等矩阵。

4. 矩阵的等价

（1）定义：若矩阵A可通过有限次的初等变换得到矩阵B，则称矩阵A与矩阵B等价。

即：A $\rightarrow$ B $\Leftrightarrow$ A ≅ B.

备注：对同型矩阵A,B，若存在可逆矩阵P,Q，使得：PAQ = B，则称矩阵A与矩阵B等价。

（2）性质：

1）反身性：对于任何矩阵A，都有A ≅ A.

2）对称性：若矩阵A与矩阵B等价A ≅ B，则矩阵B与矩阵A也等价B ≅ A.

3）传递性：若矩阵A ≅ B，B ≅ C，则A ≅ C.

（3）结论：

1）任意一个矩阵 $A_{m*n}$ 都与其标准形矩阵等价。

2）矩阵A ≅ B的充要条件是存在一系列初等矩阵 $P_{1},P_{2},...P_{s},Q_{1},Q_{2},...Q_{t}$ ,使得：

$P_{s}...P_{2}P_{1}AQ_{1}Q_{2}...Q_{t}=B$ 。

3）矩阵A ≅ B的充要条件是存在可逆矩阵 $P,Q$ ,使得： $PAQ=B$ 。

4）若矩阵A ≅ B，则矩阵A与矩阵B的标准形相同。

5）若矩阵A ≅ B，则矩阵A与矩阵B的秩相同，即r(A) = r(B)。

6）若矩阵A，B是同型矩阵，则矩阵A ≅ B的充要条件是r(A) = r(B)。

7）若矩阵A，B是同阶方阵，且A ≅ B，则 $|A|=k|B|(k\neq 0)$ 。

$\Rightarrow$ $|A|$ 、 $|B|$ 同时为0或者同时不为0。

8）若矩阵A，B是同阶方阵，且A ≅ B，则A，B同时可逆，或者同时不可逆。

9）设A为 $n$ 阶方阵，则矩阵A可逆的充要条件是A ≅ E。

10）设A为 $n$ 阶方阵，则矩阵A可逆的充要条件是矩阵A可以表示为有限个初等矩阵的乘积。

5. 逆矩阵求法

（1）方法：①：伴随矩阵法： $A^{-1}=\frac{A^{*}}{\left | A \right |}$ ；②：逆矩阵定义的推论；③：初等行变换法。

（2）初等行变换法求逆矩阵：

1）求解过程：

已知矩阵A，如下所示，判断矩阵A是否可逆，若可逆，求解矩阵A的逆矩阵。

$A=\begin{pmatrix} 1 & 1& 1 \\ 2 & 1 & 0 \\ 1& -1&0 \end{pmatrix}$ .

①：先将矩阵A与单位矩阵E进行行拼接，如下所示：

$(A,E)=\begin{pmatrix} 1 & 1& 1& : & 1 & 0&0 \\ 2 & 1 & 0 & :& 0& 1& 0\\ 1& -1&0 &: & 0& 0 & 1 \end{pmatrix}$ .

②：将拼接好的矩阵 $(A,E)$ 整体进行初等行变换，直到矩阵A被化成单位矩阵，变换过程

中，先处理第一列元素，处理完后再处理第二列，依此类推：

$\rightarrow ...\rightarrow \begin{pmatrix} 1 & 0& 0&: & 0 & \frac{1}{3}&\frac{1}{3} \\ 0& 1 & 0 &: & 0 & \frac{1}{3} &-\frac{2}{3} \\ 0& 0& 1&: & 1 &-\frac{2}{3} & \frac{1}{3} \end{pmatrix}$ .

③：将矩阵A化成单位矩阵后，则原单位矩阵E的位置的矩阵就是矩阵A的逆矩阵：

$A^{-1}=\begin{pmatrix} 0 & \frac{1}{3}&\frac{1}{3} \\ 0 & \frac{1}{3} &-\frac{2}{3} \\ 1 &-\frac{2}{3} & \frac{1}{3} \end{pmatrix}$ .

备注：若矩阵A无法化成单位矩阵，则说明矩阵A不可逆。

2）原理推导：

①：若矩阵A可逆，则 $|A|\neq 0$ ，进而有 $|A^{-1}| = \frac{1}{|A|}\neq 0$ ，所以 $A^{-1}$ 也可逆。

②：因 $A^{-1}$ 可逆，所以 $A^{-1}$ 可写成 $A^{-1}= P_{1}P_{2}...P_{s}$ 的形式。

③：对 $A^{-1}= P_{1}P_{2}...P_{s}$ 做如下处理：

$P_{1}P_{2}...P_{s}A= A^{-1}A=E$ .

$P_{1}P_{2}...P_{s}E= A^{-1}E=A^{-1}$ .

④：从上式可知，将矩阵A和单位矩阵E行拼接后，同时进行初等行变换，矩阵A化成单位矩

阵时，原单位矩阵化成 $A^{-1}$ 。

小贴士：

1. 初等行变换法求矩阵方程AX=B：

1）求解过程：

①：先将矩阵A与矩阵B进行行拼接。

②：将拼接好的矩阵 $(A,B)$ 整体进行初等行变换，直到矩阵A被化成单位矩阵。

③：将矩阵A化成单位矩阵后，则原矩阵B的位置的矩阵就是矩阵方程的解 $X=A^{-1}B$ 。

2）原理推导：

①：若矩阵A可逆，则 $|A|\neq 0$ ，进而有 $|A^{-1}| = \frac{1}{|A|}\neq 0$ ，所以 $A^{-1}$ 也可逆。

②：因 $A^{-1}$ 可逆，所以 $A^{-1}$ 可写成 $A^{-1}= P_{1}P_{2}...P_{s}$ 的形式。

③：对 $A^{-1}= P_{1}P_{2}...P_{s}$ 做如下处理：

$P_{1}P_{2}...P_{s}A= A^{-1}A=E$ .

$P_{1}P_{2}...P_{s}B= A^{-1}B=X$ .

④：从上式可知，将矩阵A和矩阵B行拼接后，同时进行初等行变换，矩阵A化成单位矩阵

时，原矩阵B化成 $X$ 。

2. 初等列变换法求矩阵方程XA=B：

1）求解过程：

①：先将矩阵A与矩阵B进行列拼接。

②：将拼接好的矩阵 $(\frac{A}{B})$ 整体进行初等列变换，直到矩阵A被化成单位矩阵。

③：将矩阵A化成单位矩阵后，则原矩阵B的位置的矩阵就是矩阵方程的解 $X=BA^{-1}$ 。

2）原理推导：

①：若矩阵A可逆，则 $|A|\neq 0$ ，进而有 $|A^{-1}| = \frac{1}{|A|}\neq 0$ ，所以 $A^{-1}$ 也可逆。

②：因 $A^{-1}$ 可逆，所以 $A^{-1}$ 可写成 $A^{-1}= P_{1}P_{2}...P_{s}$ 的形式。

③：对 $A^{-1}= P_{1}P_{2}...P_{s}$ 做如下处理：

$AP_{1}P_{2}...P_{s}= AA^{-1}=E$ .

$BP_{1}P_{2}...P_{s}= BA^{-1}=X$ .

④：从上式可知，将矩阵A和矩阵B列拼接后，同时进行初等列变换，矩阵A化成单位矩阵

时，原矩阵B化成 $X$ 。

备注：以上就是普通矩阵，不一定是方阵。

6. 分块矩阵

6.1 分块矩阵的概念

（1）常规的分块矩阵

$eg1:A = \begin{pmatrix} 1 & 2 & 0 & -1 &3 \\ 0& -1 & 1 & 2& 1\\ 0& 1& 5 & -2& 2\\ 1 & 3 & 4 & 0 & 6 \end{pmatrix} = \begin{pmatrix} A_{1} &A_{2} \\ A_{3}&A_{4} \\ A_{5} & A_{6} \end{pmatrix}$

其中： $A_{1}=\begin{pmatrix} 1 & 2&0 \end{pmatrix}$ $A_{2}=\begin{pmatrix} -1 & 3 \end{pmatrix}$

$A_{3}=\begin{pmatrix} 0 & -1&1 \\ 0 & 1&5 \end{pmatrix}$ $A_{4}=\begin{pmatrix} 2 & 1 \\ -2 & 2 \end{pmatrix}$

$A_{5}=\begin{pmatrix} 1 & 3&4 \end{pmatrix}$ $A_{6}=\begin{pmatrix} 0 & 6 \end{pmatrix}$

$eg2:A = \begin{pmatrix} 1 & 2 & 0 & -1 &3 \\ 0& -1 & 1 & 2& 1\\ 0& 1& 5 & -2& 2\\ 1 & 3 & 4 & 0 & 6 \end{pmatrix} = \begin{pmatrix} \alpha _{1} \\ \alpha_{2} \\ \alpha_{3} \\ \alpha_{4} \end{pmatrix}$

其中： $\alpha_{1} = \begin{pmatrix} 1 & 2 & 0& -1& 3 \end{pmatrix}$ $\alpha_{2} = \begin{pmatrix} 0 & -1 & 1 & 2& 1 \end{pmatrix}$

$\alpha_{3} = \begin{pmatrix} 0 & 1 & 5 & -2& 2 \end{pmatrix}$ $\alpha_{4} = \begin{pmatrix} 1 & 3 & 4 & 0& 6 \end{pmatrix}$

$eg3:A = \begin{pmatrix} 1 & 2 & 0 & -1 &3 \\ 0& -1 & 1 & 2& 1\\ 0& 1& 5 & -2& 2\\ 1 & 3 & 4 & 0 & 6 \end{pmatrix} = \begin{pmatrix} \beta _{1} & \beta_{2} & \beta_{3} & \beta_{4} \end{pmatrix}$

其中： $\beta_{1}=\begin{pmatrix} 1\\ 0\\ 0\\ 1 \end{pmatrix}$ $\beta_{2}=\begin{pmatrix} 2\\ -1\\ 1\\ 3 \end{pmatrix}$ $\beta_{3}=\begin{pmatrix} 0\\ 1\\ 5\\ 4 \end{pmatrix}$ $\beta_{4}=\begin{pmatrix} -1\\ 2\\ -2\\ 0 \end{pmatrix}$ $\beta_{5}=\begin{pmatrix} 3\\ 1\\ 2\\ 6 \end{pmatrix}$

备注：将矩阵分块是为了简化计算。

（2）特殊的分块矩阵

1）主对角线-上三角分块矩阵 2）主对角线-下三角分块矩阵

$eg1=\begin{pmatrix} A_{1} &* &... &* \\ &A_{2} &... &* \\ & &... & ...\\ & & & A_{k} \end{pmatrix}$ $eg2=\begin{pmatrix} A_{1} & & & \\ *&A_{2} & &\\ ...& ...&... & \\ *&* &... & A_{k} \end{pmatrix}$

3）主对角线-对角分块矩阵

$eg3=\begin{pmatrix} A_{1} & & & \\ &A_{2} & &\\ & &... & \\ & & & A_{k} \end{pmatrix}$

备注：上述 $A_{1}$ ， $A_{2}$ ，..., $A_{k}$ 均为方阵。

6.2 分块矩阵的运算

（1）分块矩阵的加减法

遵守原则：1）相加减的两个分块矩阵为同型矩阵且相对应位置的子块也为同型矩阵；

2）相对应位置的子块相加减。

$eg:\begin{pmatrix} A_{1}&B_{1} \\ A_{2}& B_{2} \\ A_{3}& B_{3} \end{pmatrix}\pm \begin{pmatrix} C_{1}&D_{1} \\ C_{2}& D_{2} \\ C_{3}& D_{3} \end{pmatrix}=\begin{pmatrix} A_{1}\pm C_{1}& B_{1}\pm D_{1}\\ A_{2}\pm C_{2}&B_{2}\pm D_{2} \\ A_{3}\pm C_{3}& B_{3}\pm D_{3} \end{pmatrix}$

（2）分块矩阵的数乘

遵守原则：用数 $k$ 乘以分块矩阵A，就是用数 $k$ 乘以分块矩阵A内的每一个子块。

$eg:k*\begin{pmatrix} A& B&C \\ U& V& W\\ X& Y& Z \end{pmatrix}=\begin{pmatrix} k*A& k* B&k*C \\ k*U& k* V& k*W\\ k* X&k* Y& k*Z\end{pmatrix}$

（3）分块矩阵的乘法

遵守原则：1)分块矩阵 $A_{1}$ 的列的分法与分块矩阵 $B_{1}$ 的行的分法必须相同；

2)分块矩阵 $C_{1}$ 的行数是分块矩阵 $A_{1}$ 的行数,分块矩阵 $C_{1}$ 的列数是分块矩阵 $B_{1}$ 的列数；

3)分块矩阵 $A_{1}$ 的每行子块分别乘以分块矩阵 $B_{1}$ 的每列子块，再做和，结果写到相应的

行列坐标位置上。

$eg:A_{1} = \begin{pmatrix} A & B\\ C &D \\ E & F \end{pmatrix}$ 3 x 2 $B_{1} = \begin{pmatrix} U & V& W& P\\ X& Y& Z& Q \end{pmatrix}$ 2 x 4

$C_{1}=A_{1}*B_{1}=\begin{pmatrix} AU+BX& AV+BY& AW+BZ& AP+BQ\\ CU+DX& CV+DY& CW+DZ& CP+DQ\\ EU+FX& EV+FY& EW+FZ& EP+FQ\\ \end{pmatrix}$ 3 x 4

备注：

1. 列的分法与行的分法必须相同的解释：

①：分块矩阵 $A_{1}$ 的列数与分块矩阵 $B_{1}$ 的行数相等。

②：分块矩阵 $A_{1}$ 与 $B_{1}$ 对应位置的子块(如子块A与U)，子块 $A$ 的列数与子块 $U$ 的行数相等。

2. 分块矩阵相乘时，需要保证左边分块矩阵的子块在左边，右边分块矩阵的子块在右边。

6.3 分块矩阵的转置

若分块矩阵A为：↓↓↓↓↓↓ 则分块矩阵A的转置为：↓↓

$A=\begin{pmatrix} A_{1} & A_{2} &A_{3} \\ A_{4} & A_{5} & A_{6} \\ A_{7} &A_{8} & A_{9} \end{pmatrix}$ $A^{T}=\begin{pmatrix} A_{1}^{T} & A_{4}^{T} &A_{7}^{T} \\ A_{2}^{T} & A_{5}^{T} & A_{8}^{T} \\ A_{3}^{T} &A_{6}^{T} & A_{9}^{T} \end{pmatrix}$

6.4 分块矩阵的行列式

若矩阵A为 $m$ 阶方阵，矩阵B为 $n$ 阶方阵，则：

（1）主对角线-上三角、下三角、对角分块矩阵的行列式：

$\left | \begin{pmatrix} A &C \\ O & B \end{pmatrix} \right |=\left | \begin{pmatrix} A &O \\ C & B \end{pmatrix} \right |=\left | \begin{pmatrix} A &O \\ O & B \end{pmatrix} \right | = |A|*|B|$ .

（2）副对角线-上三角、下三角、对角分块矩阵的行列式：

$\left | \begin{pmatrix} C &A \\ B & O \end{pmatrix} \right |=\left | \begin{pmatrix} O &A \\ B & C \end{pmatrix} \right |=\left | \begin{pmatrix} O &A \\ B & O \end{pmatrix} \right | =(-1)^{mn} |A|*|B|$ .

6.5 分块矩阵的逆矩阵

（1）若分块矩阵 $A = \begin{pmatrix} B &O \\ O& C \end{pmatrix}$ ,矩阵B和矩阵C均可逆，则 $A^{-1} = \begin{pmatrix} B^{-1} &O \\ O& C^{-1} \end{pmatrix}$ 。

（2）若分块矩阵 $A = \begin{pmatrix} O &B \\ C& O\end{pmatrix}$ ,矩阵B和矩阵C均可逆，则 $A^{-1} = \begin{pmatrix} O&C^{-1} \\ B^{-1}&O \end{pmatrix}$ 。

（3）设矩阵A和矩阵B为方阵，则分块矩阵 $\begin{pmatrix} A &C \\ O& B \end{pmatrix}$ 可逆 $\Leftrightarrow$ 矩阵A和矩阵B均可逆，且逆矩阵：

$\begin{pmatrix} A &C \\ O& B \end{pmatrix}^{-1}=$ $\begin{pmatrix} A^{-1} & -A^{-1}CB^{-1} \\ O& B^{-1} \end{pmatrix}$ 。

（4）设矩阵A和矩阵B为方阵，则分块矩阵 $\begin{pmatrix} A &O \\ C& B \end{pmatrix}$ 可逆 $\Leftrightarrow$ 矩阵A和矩阵B均可逆，且逆矩阵：

$\begin{pmatrix} A &O \\ C& B \end{pmatrix}^{-1}=$ $\begin{pmatrix} A^{-1} &O \\ -B^{-1}CA^{-1}& B^{-1} \end{pmatrix}$ 。

7. 矩阵的秩

7.1 矩阵的秩的概念

（1）矩阵的 $k$ 阶子式

设矩阵A为 $m$ X $n$ 的矩阵，在矩阵A中任取 $k$ 行 $k$ 列，位于这些行列交叉点的 $k^{2}$ 个元素，按照它们原来的位置进行重组，得到的行列式称为矩阵A的一个 $k$ 阶子式。

备注： $k$ ≤ min( $m$ , $n$ )。

（2）矩阵的秩

矩阵A中非零子式的最高阶数，称为矩阵A的秩，记作 $r$ (A)。

备注：

1. 非零子式就是指行列式的值不为0的子式。

2. 对于任意矩阵，有 0 ≤ $r$ (A) ≤ min( $m$ , $n$ )。

3. 对于任意 $O$ 矩阵，有 $r$ ( $O$ ) = 0。

4. 对于任意非 $O$ 矩阵A，有 $r$ (A) ≥ 1。

（3）满秩矩阵

设矩阵A为 $m$ X $n$ 的矩阵，若 $r$ (A) = min( $m$ , $n$ )，则称矩阵A为满秩矩阵。

备注：①：若 $r$ (A) = $m$ ，则称矩阵A为行满秩矩阵。

②：若 $r$ (A) = $n$ ，则称矩阵A为列满秩矩阵。

（4）降秩矩阵

设矩阵A为 $m$ X $n$ 的矩阵，若 $r$ (A) ＜ min( $m$ , $n$ )，则称矩阵A为降秩矩阵。

小贴士：

若矩阵A为 $n$ 阶方阵，则有：

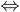
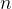
①：矩阵A满秩 $\Leftrightarrow$ $r$ (A) = $n$ $\Leftrightarrow$ |A| ≠ 0 $\Leftrightarrow$ 矩阵A可逆。

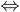
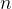
②：矩阵A降秩 $\Leftrightarrow$ $r$ (A)＜ $n$ $\Leftrightarrow$ |A| = 0 $\Leftrightarrow$ 矩阵A不可逆。

可通过此结论求解矩阵A的秩。